1.数组中重复的数字

思路1：

使用哈希表，哈希表是一种根据关键码（key）直接访问值（value）的一种数据结构。而这种直接访问意味着只要知道key就能在O(1)时间内得到value，因此哈希表常用来统计频率、快速检验某个元素是否出现过等。
step 1：遍历数组，将没有出现过的元素加入哈希表。
step 2：遇到的元素在哈希表中出现过就是重复数组。
step 3：遍历结束也没找到就返回-1.

import java.util.*;
public class Solution {
    public int duplicate (int[] numbers) {
        //哈希表记录重复
        HashMap<Integer, Integer> mp = new HashMap<>();
        //遍历数组
        for(int i = 0; i < numbers.length; i++){
            //如果没有出现过就加入哈希表
            if(!mp.containsKey(numbers[i]))
                mp.put(numbers[i], 1);
            //否则就是重复数字
            else
                return numbers[i];
        }
        //没有重复
        return -1;
    }
}

复杂度

时间：O(n)，其中n为数组长度，遍历一次数组，哈希表每次操作都是O(1)
空间：O(n)，哈希表最大的空间为数组长度

思路2（#）：

既然数组长度为nnn只包含了0到n−1n-1n−1的数字，那么如果数字没有重复，这些数字排序后将会与其下标一一对应。那我们就可以考虑遍历数组，每次检查数字与下标是不是一致的，一致的说明它在属于它的位置上，不一致我们就将其交换到该数字作为下标的位置上，如果交换过程中，那个位置已经出现了等于它下标的数字，那肯定就重复了。

2.二维数组中的查找

思路1（暴力）:直接遍历数组寻找

public class Solution {
    public boolean Find(int target, int [][] array) {
        //逐行逐列遍历
        for(int i=0;i<array.length;i++){
            for(int j=0;j<array[0].length;j++){
                if (array[i][j]==target){
                    return true;
                }
            }
        }
        return false;
    }
}

复杂度

时间：O(n^2) 空间：O(1)

思路2：循环一次，从左下角开始查找。

对于左下角的值 m，m 是该行最小的数，是该列最大的数。
step 1：首先获取矩阵的两个边长，判断特殊情况。
step 2：首先以左下角为起点，若是它小于目标元素，则往右移动去找大的，若是他大于目标元素，则往上移动去找小的。
step 3：若是移动到了矩阵边界也没找到，说明矩阵中不存在目标值。
用某行最小或某列最大与 target 比较，每次可剔除一整行或一整列。

public class Solution {
    public boolean Find(int target, int [][] array) {
        int rows = array.length;
        if(rows == 0){
            return false;
        }
        int cols = array[0].length;
        if(cols == 0){
            return false;
        }
        // 左下
        int row = rows-1;
        int col = 0;
        while(row>=0 && col<cols){
            if(array[row][col] < target){
                col++;
            }else if(array[row][col] > target){
                row--;
            }else{
                return true;
            }
        }
        return false;
    }
}

3.替换空格

思路1：

将字符串遍历成一个个字符，存储到StringBuilder中。如果遇到空格则替换成%20。

public String replaceSpace(String s) {
    StringBuilder stringBuilder = new StringBuilder();
    for (int i = 0; i < s.length(); i++) {
        if (s.charAt(i) == ' ')
            stringBuilder.append("%20");
        else
            stringBuilder.append(s.charAt(i));
    }
    return stringBuilder.toString();
}

复杂度

时间和空间复杂度都是O(n)

思路2：

将字符串存到字符数组里面（char[])，然后依次遍历字符数组中的值，遇到空格则添加三个字符。

public String replaceSpace(String s) {
    int length = s.length();
    char[] array = new char[length * 3];
    int index = 0;
    for (int i = 0; i < length; i++) {
        char c = s.charAt(i);
        if (c == ' ') {
            array[index++] = '%';
            array[index++] = '2';
            array[index++] = '0';
        } else {
            array[index++] = c;
        }
    }
    String newStr = new String(array, 0, index);
    return newStr;
}

复杂度

时间和空间复杂度都是O(n)

4.从尾到头打印链表

思路1：递归

新建一个list，在递归里面，判断链表的next是否为空，不为空把值放进list(因为是递归，所以add的时候会将链表从最后一个值开始add到list)，跳出递归的条件式链表的next为空，返回list。

import java.util.*;
public class Solution {
    ArrayList<Integer> list = new ArrayList();
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        if(listNode!=null){
        //因为这里用的是递归，所以方法中会从list的最后一个非空值开始存，直到第一个。
            printListFromTailToHead(listNode.next);
            list.add(listNode.val);
        }
        return list;
    }
}

复杂度

时间，空间复杂度为O(n)

思路2：非递归

创建一个list，直接将每次链表next得到的值插入到list的首位–>使用list.add(0,value)的方式。

import java.util.ArrayList;
public class Solution {
        ArrayList<Integer> list = new ArrayList<Integer>();
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
    //注意这里是while(和上面的递归区分一下）
        while(listNode!=null){
            list.add(0,listNode.val);
            listNode = listNode.next;
        }
        return list;
    }
}

复杂度

时间，空间复杂度为O(n)

思路3：

反转链表，将链表的值放到list中，然后直接反转list即可。

import java.util.ArrayList;
import java.util.Collections;
public class Solution {
        ArrayList<Integer> list = new ArrayList<Integer>();
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
while(listNode!=null){
            list.add(listNode.val);
            listNode=listNode.next;
        }
        Collections.reverse(list);
        return list;
    }
    }

5.重建二叉树

思路1：

例如：
前序序列{1,2,4,7,3,5,6,8} = pre
中序序列{4,7,2,1,5,3,8,6} = in
通俗理解：
1）根据先序遍历找到根节点，然后在中序遍历中找对这个根节点，中序遍历左边的所有节点都是根的左子树，右边为右子树。
2）确定左子树的子节点：根据中序遍历里根节点以左的所有节点，找到先序遍历里顺序排在前面的第一个节点，即为该根节点的左子树
3）然后以该左子树作为根，重复1）和2）步骤即可。

代码理解：
1)在先序中找到根节点，对应找到该节点在中序遍历中的位置
2）确定根的左子树：左子树前序遍历{2,4,7}，中序遍历为{4,7,2}；确定跟的右子树：右子树前序遍历{3,5,6,8}，中序遍历为{5,3,8,6}
3)子树同上述操作

import java.util.Arrays;
public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        if (pre.length == 0 || in.length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(pre[0]);
        // 在中序中找到前序的根
        for (int i = 0; i < in.length; i++) {
            if (in[i] == pre[0]) {
                // 左子树，注意 copyOfRange 函数，左闭右开
                root.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i + 1), Arrays.copyOfRange(in, 0, i));
                // 右子树，注意 copyOfRange 函数，左闭右开
                root.right = reConstructBinaryTree(Arrays.copyOfRange(pre, i + 1, pre.length), Arrays.copyOfRange(in, i + 1, in.length));
                break;
            }
        }
        return root;
    }
}

复杂度

时间，空间复杂度为O(n)

6.二叉树的下一个结点（#）

思路：

我们首先要根据给定输入中的结点指针向父级进行迭代，直到找到该树的根节点；然后根据根节点进行中序遍历，当遍历到和给定树节点相同的节点时，下一个节点就是我们的目标返回节点。
具体做法：
step 1：首先先根据当前给出的结点找到根节点
step 2：然后根节点调用中序遍历
step 3：将中序遍历结果存储下来
step 4：最终拿当前结点匹配是否有符合要求的下一个结点

import java.util.*;
public class Solution {
    ArrayList<TreeLinkNode> nodes = new ArrayList<>();
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        // 获取根节点
        TreeLinkNode root = pNode;
        while(root.next != null) root = root.next;
         
        // 中序遍历打造nodes
        InOrder(root);
         
        // 进行匹配
        int n = nodes.size();
        for(int i = 0; i < n - 1; i++) {
            TreeLinkNode cur = nodes.get(i);
            if(pNode == cur) {
                return nodes.get(i+1);
            }
        }
        return null;
    }
     
    // 中序遍历
    void InOrder(TreeLinkNode root) {
        if(root != null) {
            InOrder(root.left);
            //将中序遍历的结果存起来
            nodes.add(root);
            InOrder(root.right);
        }
    }
}

复杂度

时间，空间复杂度为O(n)

7.用两个栈实现队列

思路：

1）往队列尾部插入值时，对应的栈操作为：直接都压入stack1
2) 往队列头部删除值时：

如果stack2位空，先将stack1的所有值压入stack2，然后弹出stack2的栈顶；
如果stack2不为空，直接弹出栈顶即为删除队头。

import java.util.Stack;

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
    public void push(int node) {
        stack1.push(node);
    }
    
    public int pop() {
        //如果stack2为空，把stack1所有的值弹出放到stack2
        if(stack2.size()==0){
            //注意用while
            while(stack1.size()>0){
                stack2.push(stack1.pop());
            }
        }
           return stack2.pop();
    }
}

复杂度

时间：push的时间复杂度为O(1)，pop的时间复杂度为O(n)，push是直接加到栈尾，相当于遍历了两次栈
空间：O(n)，借助了另一个辅助栈空间

8.斐波那契数列

动态规划算法的基本思想：将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解；对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。

思路：

每次就用到了最近的两个数，所以我们可以只存储最近的两个数。
sum 存储第 n 项的值
one 存储第 n-1 项的值
two 存储第 n-2 项的值
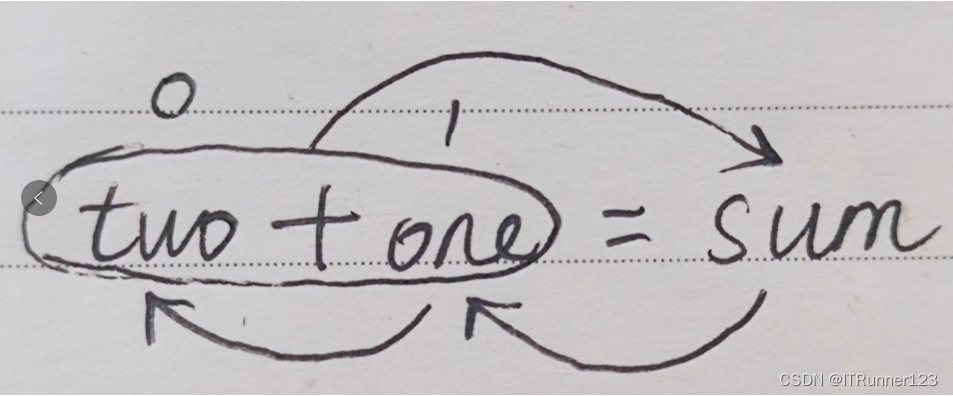
在这里插入图片描述

public class Solution {
    public int Fibonacci(int n) {
        if(n == 0){
            return 0;
        }else if(n == 1){
            return 1;
        }
        int sum = 0;
        int two = 0;
        int one = 1;
        for(int i=2;i<=n;i++){
            sum = two + one;
            two = one;
            one = sum;
        }
        return sum;
    }
}

9.旋转数组的最小数字

思路：（二分法）

1）设置数组的首尾位置作为区间端点
2）取区间中点，若大于末尾端点，则最小值一定在中点右边；
3）中点若等于末尾端点，不确定哪边的小（1,0,1,1,1或者1,1,1,0,1）所以末尾端点向前推一位；
4）中间若小于末尾端点，最小值一定在中点左边或者中点。

import java.util.ArrayList;
public class Solution {
    public int minNumberInRotateArray(int [] array) {
        int left = 0;
        int right = array.length - 1;
        while(left < right){
            int mid = (left + right) / 2;
            //最小的数字在mid右边
            if(array[mid] > array[right])
                left = mid + 1;
            //无法判断，一个一个试
            else if(array[mid] == array[right])
                right--;
            //最小数字要么是mid要么在mid左边（注意这里的mid不能减1，特例：1,0,1,1,1）
            else if(array[mid] < array[right])
                right = mid;
        }
        return array[left];
    }
}

复杂度

时间：O(log2n)，二分法最坏情况对nnn取2的对数。
空间：O(1)，常数级变量，无额外辅助空间。

10.矩阵中的路径（##）

思路（递归，回溯法）：

要在矩阵中找到从某个位置开始，位置不重复的一条路径，路径为某个字符串，那我们肯定是现在矩阵中找到这个位置的起点。没办法直观的找出来，只能遍历矩阵每个位置都当作起点试一试。找到起点后，它周围的节点是否可以走出剩余字符串子串的路径，该子问题又可以作为一个递归。因此，可以用递归来解决。

import java.util.*;
public class Solution {
    private boolean dfs(char[][] matrix, int n, int m, int i, int j, String word, int k, boolean[][] flag){
        if(i < 0 || i >= n || j < 0 || j >= m || (matrix[i][j] != word.charAt(k)) || (flag[i][j] == true))
            //下标越界、字符不匹配、已经遍历过不能重复
            return false;
        //k为记录当前第几个字符
        if(k == word.length() - 1)
            return true;
        flag[i][j] = true;
        //该结点任意方向可行就可
        if(dfs(matrix, n, m, i - 1, j, word, k + 1, flag)
          ||dfs(matrix, n, m, i + 1, j, word, k + 1, flag)
          ||dfs(matrix, n, m, i, j - 1, word, k + 1, flag)
          ||dfs(matrix, n, m, i , j + 1, word, k + 1, flag))
            return true;
        //没找到经过此格的，此格未被占用
        flag[i][j] = false;
        return false;
    }
     
    public boolean hasPath (char[][] matrix, String word) {
        //优先处理特殊情况
        if(matrix.length == 0)
            return false;
        int n = matrix.length;
        int m = matrix[0].length;
        //初始化flag矩阵记录是否走过
        boolean[][] flag = new boolean[n][m];
        //遍历矩阵找起点
        for(int i = 0; i < n; i++){ 
            for(int j = 0; j < m; j++){
                //通过dfs找到路径
                if(dfs(matrix, n, m, i, j, word, 0, flag))
                    return true;
            }
        }
        return false;
    }
}