交通 | 动态设施选址问题

在这里插入图片描述

论文解读陈迎新，柯斯琪，曲晨辉，张景琪

编者按

本次解读的文章是Transportation Science 2017年的《在日益增长的市场中，动态设施选址问题的连续逼近方法》（Wang, X., Lim, M. K., & Ouyang, Y. (2017). A continuum approximation approach to the dynamic facility location problem in a growing market. Transportation Science, 51(1), 343-357.）

原文摘要总结如下：

本文所需要解决的问题是在大规模增长市场的情况下，如何确定最佳的设施位置和部署时间，以便在规划范围内尽量减少设施建设和客户服务的成本。

为了克服计算上的挑战，本文采用了连续逼近（continuum approximation, CA）模型来解决大规模增长市场的动态设施选址问题，通过CA模型确定了时空连续体中的最佳设施密度。其次，本文提出了管子模型（Tube model），将得到的连续设施密度函数离散为一组时变的设施位置轨迹。再者，为了保证设施位置的一致性，本文采用了一种基于惩罚方法的迭代调节程序（iterative regulation procedure）。同时，文章也证明了上述方法的收敛性，并进一步推导了CA方法和管子模型产生紧密的近似误差界的条件。最后，文章也进行了一系列的数值实验来说明所提出的建模框架的适用性和计算性能（例如，准确性和收敛性），具体而言是通过与使用假设数据的离散模型进行比较，然后应用于伊利诺伊州的经验案例。

1. 写在前面

静态设施选址 vs 动态设施选址

设施选址决策对商业实践中的许多问题至关重要，一般而言决策者（如政府或公司）需要找到一组设施（如消防站或当地分支机构）的空间分布，以尽量减少满足各种需求的总成本（如设施和运输成本）。设施选址决策通常意味着对大量资源的长期承诺，即一旦做出了决定（设施已经开放），决策很难轻易被逆转。

即使不考虑设施位置决策的长期性影响，大量的研究因计算上的挑战仍集中在静态设施位置问题上（其中参数随时间是恒定的）。然而，在现实中，系统的任何参数（例如，客户需求、运营成本）都可能会随着时间的推移而变化，而设施的增加可能会在不同的时间发生。也就是说，“在哪里”和“在何时”均为建设设施的关键决定。

在本文中，学者探讨了一类动态的设施布局规划问题，其中一个中央规划者试图确定设施布局的最佳位置和时间，以尽量减少在各规划阶段的累积物流成本。特别是，文章考虑了一个需求不断增长的市场环境（而单位运营成本可能会降低），故新的设施会随着时间的推移不断开放或增加。本文的研究目的是提供一种适合大规模实例的动态设施布局规划的有效解决方法。

相关设定与问题的数学表达
假设一组设施由编号 i =1,2，…表示，这些设施于有限的时间规划范围 $\Psi=[0,T]$ 内在连续且紧(continuous and compact)的服务区域 $\Omega⊆ R^2$ 开放。客户的需求被假设为一个服从连续分布的密度函数。设施 i 将在 $\tau_{i}\in\Psi$ 时刻的 $x_{i}\in \Omega$ 位置开放，覆盖其服务区域 $S_{i}(t)⊆ \Omega$ 为所有 $\in \Psi$ 的一组客户。假设每个客户都由一个单一的设施提供服务，因此 ${S_{i}(t)\}_i$ 在任何时间 t 形成一个 Ω 的分区。

文章认为系统总成本包括三个部分：一次性固定设施投资成本、基于运营时间的运营成本和运输成本。
假设在 t 时刻的位置 x 附近，固定投资为$h(x, t) $；按比例分摊的客户服务成本包括设施运营成本和单位时间单位面积运输成本，即$ z(x, x_i, S_i(t),t)$。考虑到货币的时间价值，这两个成本函数都被转换为现值。此外，本文假设开放的设施不能关闭或搬迁（Current, Ratick, and ReVelle 1997）。

为了方便起见，文章定义了 $S_i:=\{ S_i(t)\}_t$ 。然后，系统设计的位置、服务区域和时间等方面的决策分别用 ${x_i\}_i$ 、 ${S_i\}_i$ 和 $\{\tau_i\}_i$ 表示。

因此，一个动态设施位置问题的一般形式如下:
$min_{ \{x_i\}_i，\{S_i\}_i，\{\tau_i\}_i}P = \int_\Psi\int_\Omega z(x, x_i, S_i(t),t)dxdt+\sum_{i}h(x_i, \tau_i) (1) \\ \\ s.t. S_i(t) = \empty, \forall i, t\in[0,\tau_i), (2) \\ S_{i1}(t)\cap S_{i2}(t) = \empty, \forall i_1 \neq i_2 , t (3)\\ \\ \cup_{\forall i } S_i(t) = \Omega, \forall t (4)\\ \\ \tau_i \in \Psi,x_{i} \in \Omega, \forall i (5)$

目标函数(1)是将整个时空连续体 $\Omega * \Psi$ 上的总客户服务成本和固定设施投资成本之和最小化。约束条件(2)是强制执行服务区域在构建相应的设施之前应该是一个空集。约束条件(3)-(4)是规定，开放设施的服务区域集的交始终为无重叠的 $\Omega$ 分区。假设客户总是由最近的设施提供服务，且连接关系可以被任意打破。

CA模型不能直接应用于动态问题

尽管CA已被广泛用于解决静态设施位置问题，但为处理这些问题的动态版本所做的工作相对较少。机器人社区已经做了一些相关的尝试；例如，

Ny和Pappas（2010）提出了一种自适应算法来解决动态车辆路径问题，给定随机即将到来的客户位置的概率分布。
Cambell（1990）注意到CA背后的主要思想是定位空间决策，他将CA扩展到动态设置下设计运输终端，但假设终端位置是“移动的”，可以在每次瞬间独立移动。

然而，在现实中，开放设施的位置在规划范围的其余部分通常保持不变。我们将其称为位置一致性约束。由于这种限制，设施部署决策会对剩余的规划范围产生持续的影响，并且不能通过时间邻域中的局部参数来确定。此外，即使使用CA获得了DFLP的解决方案，仍然需要一种转换方法来有效地将CA解决方案在时间和空间上转换为离散的设施位置。上述的磁盘模型（Ouyang和Daganzo 2006）是为静态问题而设计的，因此不能直接应用于动态问题。

2. 模型构建

2.1 连续逼近

首先，我们对DFLP离散模型进行连续逼近。假设：

对位置一致约束（location consistency constraint）进行松弛。位置一致约束（location consistency constraint）指已经开放的设施位置保持不变。
空间Ω足够大，并且客户服务成本 z 和固定成本 h 都相对于空间和时间缓慢变化
那么，
最优的空间服务区域应该是尽可能的 "圆"的
区域大小可以用一个缓慢变化的平滑函数来近似表示, $|S_i(t)|, for x \in S_i(t)$
客户服务成本 $z(x, x_i, S_i(t))$ 可以用一个缓慢变化的函数 $z_C(x, A(x,t), t)$ 来近似
设施的固定成本可以在时间和空间上按比例分配为 $h(x, t) [A(x, t)T]^{-1}$

于是，我们可以将DFLP 模型重构为：
$min_{A(x,t)}P_C = \int_\Psi\int_\Omega p_C(x,A(x,t),t)dxdt \\ s.t. A(x,t) >= 0, \forall x \in \Omega, t \in \Psi$
其中 $p_C(x,A(x,t),t)=z_C(x,A(x,t),t)+h(x, t) [A(x, t)T]^{-1}$ 。

首先讨论对上述模型在所有参数在时间和空间上恒定的同质系统的求解。

假设在一个同质系统中，忽略了随时间的变化，我们就可以得到：

固定成本 $h （ x, t ） \equiv h$
客户服务成本 $z_C(x, A(x,t), t)≡z_C(A(x,t))$ 是关于服务区域大小的一个函数
于是，该问题就退化成为了一个简单的静态设施选址问题：
$min_{A>= 0}P_C(A) = z_C(A) + h(AT)^{-1}$
其中，最优服务范围 $A^*$ 满足一阶求导条件：
$\frac{d}{dA}[z_C(A)] - h(A^2T)^{-1} = 0$

对于一般的异质系统，在位置 $\in \Omega$ 和时间 $ t \in \Psi$附近的最佳服务区域大小函数 $A^*(x,t)$ 可以由 $（ x, t ）$ 处的局部参数为输入的同质系统的解近似得到：
$\frac{\partial}{\partial A}[z_C(x, A^*(x,t), t)] - T^{-1}h(x,t)[A^*(x,t)]^{-2} = 0, \forall x, t$

2.2 管子模型

为了便于记述，我们将

$n_0 = n(0)$ 和 $n_T = n(T)$ 分别表示在规划范围开始和结束时开放的设施数量
$\tau_i$ 是开放设施 $i$ 的时间
将整个规划范围 $\Psi$ 划分为 $n_T - n(0) + 1$ 层
- ${\Psi : [\tau_{n_0 + j -1}, \tau_{n_0 + j}], j \in J}$ ，其中 $J = \{1, 2, 3, ..., n_T - n_0 + 1\}$
- $l_j = |\Psi_j|$ 是第 $j$ 层的长度

在本篇章中，我们采取的主要方法是通过加入时间维度，将磁盘模型Disk Model（Ouyang and Daganzo 2006）扩展为管子模型Tube Model。

首先，我们来介绍一下Disk Model。

假设给定CA模型的输出，最佳服务区域大小函数 $A^*（x）, \forall x \in \Omega $:

首先，磁盘模型生成一组磁盘作为初始近似值, 磁盘的数量近似为 $\int_\Omega [A^*(x)]^{-1} dx$ ，并且随机选定每个磁盘的中心位置为 $x_i$ 。
然后，如果一个磁盘与另一磁盘或 $\Omega$ 的边界有部分重叠，我们就对其施加排斥力，排斥力和磁盘的大小根据磁盘的位置进行更新。

这个迭代过程重复进行，直到找到一个不重叠的磁盘的平衡分布，如下图1(b)所示。
[图片]

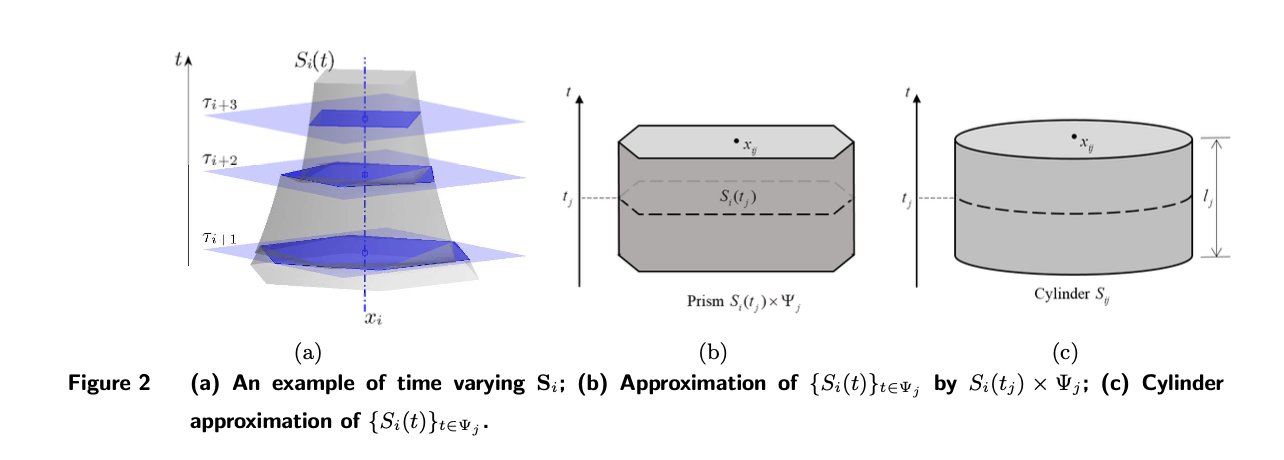
当我们将时间维度结合到磁盘模型中的时候，我们就得到了管子模型，如下图2(a)所示。假设：

在缓慢变化的参数下，每个开放设施的服务区域不会随着时间的推移而有很大的变化，除非附近区域有新的设施开放。因此，我们可以用一个棱柱来近似地描述 $j$ 层内一个开放设施的服务区域，如下图2(b)所示。
又因为 $S_i(t_j)$ 可以用一个磁盘来近似，所以所有在 $\in J$ 层的开放设施 $i$ 的服务区域可以用一个圆柱近似，如下图2©。

但是，因为我们对DFLP离散模型进行连续逼近的时候对位置一致约束（location consistency constraint）进行了松弛，于是我们可能得到一个有弧度的管子，如图3(b)所示。考虑现实情况，一个已经开放的设施位置一般是保持不变的，我们期望得到的是一个中心位置不移动的管子，如图3(a)所示。于是，我们提出了管子模型的迭代调节算法(Iterative Tube Regulation Algorithm)。
[图片]

2.3 管子模型的迭代调节算法

本文采取的方法是：允许设施的位置随时间变化，并通过在目标中施加惩罚项来强制执行约束条件。
因而，我们可以将Tube Regulation Problem建模为：

$min_{\{x_{ij}\}_{\forall x,y},\{S_i(t_j)\}_{\forall i, j}} \sum_{j\in J}\{l_j \int_\Omega z(x, x_{ij}, S_i(t_j),t_j) + h(x_{n_o + j -1, j}, t_j)\}dx + \sum_{i=1}^{n_0 - 1}h(x_i1, t_1) + \sum_{\forall i } \sum_{j = max\{i-n_0+1, 1\}}^{n_T-n_0+1}\Phi(\lambda_{ij}||x_{ij}-x_{i}||)$

$S_i(t_j) = \empty, \forall i, j < i-n_0 + 1$

$S_{i1}(t_j)\cap S_{i2}(t_j) = \empty, \forall i1 \neq i2 , j$

$\cup_{\forall i } S_i(t_j) = \Omega, \forall j$

$x_{ij} \in \Omega, \forall i, j$

本文通过以下步骤来求解上述模型：

我们在每个迭代 $k$ 中增加惩罚系数 $\lambda_{ij} > 0, \forall i, j$ ，例如，可以使其与 $\sqrt k$ 成正比。随着 $\lambda_{ij}$ 的增加， $x_{ij}$ 的可行区域缩小，这迫使圆柱体向中心对齐，因此，相应的管子变得不那么倾斜。然而，这可能会导致圆柱体之间有更大程度的重叠。这实际上是系统成本和设施位置一致性要求之间的权衡。
在迭代的每一步，对于每一层 $j$ ，所有的排斥力都是根据当前的位置和圆柱体的尺寸计算的，如下图4(a)所示。于是在迭代的每一步，基于排斥力，我们通过移动每个圆柱体和管子来找到最佳位移作为TRP在迭代 $k$ 的解决方案.

提出的DFLP算法小结

步骤1：DFLP到CA

松弛位置一致约束，将DFLP按时间点分解为无穷个独立的静态问题；
通过CA重构并求解所有静态问题，获得基于时空间的最优设施密度；
利用最优设施密度函数确定:（i）最优设施数量；（ii）设施开放时间。

步骤2：CA到level-Based DFLP

离散化时间区间，利用管子模型求解每个时间间隔的设施选址问题；
利用圆柱体近似设施服务区域，获得一系列倾斜的管子，给出本问题的松弛解。

步骤3：level-Based DFLP到DFLP

加入位置一致约束对管子的倾斜进行惩罚，将步骤2.2中的松弛解作为初始解；
更新管子的位置直到倾斜度进入可接受范围。

3. 近似误差界

本段介绍了如何评估解决方案的近似误差，并探讨了最优动态设施选址问题的上限和近似的下限。

在使用本文提出的方法时，会得到两个解：

来自第2.1节通过连续近似模型得到的CA解，该解不一定是可行解；
来自第2.3节的通过管子模型转换后得到的可行离散解。其中，可行离散解的目标值提供了原始DFLP的上限，而CA解的目标值则给出了一类离散解的下限（在某些条件成立时）。

我们可以通过一个DFLP例子来分析其最终解的上限和下限（类似的分析和证明可以应用在其他DFLP上），以下述DFLP问题为例：

靠近地址 $x$ 处，在时间 $t$ 时，顾客需求函数是 $D (x, t)$ ，设施运营成本是 $C (x, t)$ 。假设顾客总是会选择最近的设施，且交通成本是1每单位距离。该DFLP的目标函数是
$\int_{\Psi}\sum_i\int_{S_i(t)}\Vert x-x_i\Vert D(x,t)dxdt + \int_\Psi\sum_iC(x_i,t)dt + \sum_ih(x_i,\tau_i)$

我们设 $P^*$ 为真实的最优值：

可行离散解的目标值提供了该DFLP的上限：假设由管子模型得到的解的目标值为 $\hat{P}^*$ 。因为该解是可行的，我们有 $P^*\leq\hat{P}^*$ 。
CA解的目标值给出了DFLP离散解的下限：在服务范围大小为 $A (x, t)$ 的区域 $S_i(t)$ 内（区域假定为圆形），平均行驶距离是 $2/(3\sqrt{\pi})A^{1/2}(x,t)$ 。

因此，在CA模型中的服务成本为
$z_C(x,A(x,t),t)=\frac{2}{3\sqrt{\pi}}D(x,t)A^{1/2}(x,t) + C(x,t)A^{-1}(x,t)$

单位地域单位时间内的CA模型的目标函数是
$p_C(x,A(x,t),t) = \frac{2}{3\sqrt{\pi}}D(x,t)A^{1/2}(x,t) + C(x,t)A^{-1}(x,t) + \frac{1}{T}h(x,t)A^{-1}(x,t)$

我们对 $A$ 求 $p_C$ 的一次和二次偏导，得到关于最优服务范围大小的方程：
$A^*(x,t) = \begin{cases} [\frac{3\sqrt{\pi}}{D(x,t)T}(C(x,t)T + h(x,t))]^{2/3}, & \text{if} \frac{\partial^2}{\partial A^2}[p_C(x,A(x,t),t)]\vert_{A(x,t)=A^*(x,t)} > 0\\ \infty, & \text{otherwise.}\\ \end{cases}$

由此，我们也可以得到CA解的目标值为：
$P^*_C = \int_\Psi\int_\Omega p_C(x,A^*(x,t),t)dxdt$ 。

论文指出在以下三种条件均满足的情况下， $P^*_C \leq P^*$ ：

$\forall i \text{ and }t, x_i$ 是 $S_i$ 的中心
对于给定时间 $t$ ，在任一服务区域 $S_i(t)$ ，顾客需求 $D (x, t)$ 是恒定的 $D_i(t)$ ，并且运营成本 $C (x, t)$ 对 $x$ 是凹的
固定成本 $h (x, t)$ 属于以下某一种情况：对于总体的服务成本是可忽略不计的；随着时间推移减小；远大于总体服务成本；对于所有 $x, t$ 都是恒定的

最终通过证明DFLP满足以上三种情况，得证 $P^*_C \leq P^*$ ，则“CA解的目标值给出了DFLP离散解的下限“得证。详细证明过程请参考原论文。

4. 数值实验

论文使用数字算例进行了实验，希望说明CA框架的实用性，探索异质性的影响。此外，论文将提出的方法应用于伊利诺伊州的一个案例研究，以突出其对现实世界问题的适用性。

4.1 举例说明

最佳设备部署时间n(x,t)是通过连续体近似法得到的，如下图(a)所示。

该算例说明，最开始时建议部署5个设施，即 $n_0=5$ 。随后，增加四个额外的设施，直到规划期结束，即 $n_T=9$ 。具体来说，我们有 $\tau_i=0,i=1,2,3,4,5, \tau_6=0.56,\tau_7=3.69,\tau_8=6.37,\tau_9=8.72$ 。上图(b)和©分别说明了 $t = 0$ 和 $T$ 时的最优服务区域。

下面说明管子模型是如何实现的。
[图片]

图6(a)-6(d)展示了管子调节程序的一些快照。为了清楚地说明问题，管子的每个圆柱体都简单地表示在一个平面上，同一管子的圆柱体通过线条连接。

每个子图中的五个平面代表了新设施建设的时间，其中Voronoi图捕获每个设施的服务区域（即我们让顾客选择最近的设施）。方形标记代表设施位置 $x_{ij}$ ，第一层的星星标记给出了每个管子的中心。上图(d)所示收敛方案是在581次迭代后达到的，其中 $\bar{x}_i$ 为 $x_i$ 的近似值。此外，根据第三节的讨论，我们可以计算出问题的上界和近似下界。对于这个例子来说，最佳总成本的近似上界和下界分别为2544.4和2683.5，说明误差为5.47%。

4.2 异质性的敏感性实验

为说明异质性的影响，我们解决了一系列的DFLPs，每个异质性参数从0增加到0.5，其他参数固定为0。下图显示了每一类异质性的总成本的相对差异。由于我们的CA方法对DFLP的求解不一定唯一，因此对每个实例求解五次，并画出平均值。结果显示，总成本随着空间异质性的增加而减少，需求密度的异质性影响最明显。相比之下，我们发现总成本随着时间异质性的增加而上升。由于需求密度变化较快，设施运营或开放的成本随着时间的推移下降较快，保持低成本变得更加有挑战性。

[图片]

4.3 伊利诺伊州案例研究

在本小节中，我们对伊利诺伊州实施所提出的解决方法，并说明其对现实环境的适用性。
在这里插入图片描述

图8(a)显示了2014年伊利诺伊州各县的玉米年产量。所提出的方法在运行10次后得到了最优 $\hat{P}^*=4.67×10^5$ ，优化差距为3.2%，平均CPU时间为140秒。我们观察到总共开设了12个终端，其中3个是在开始时(t=0)开设的，另外4个是在剩余的时间范围 $t\in(0,20]$ 中逐渐增加的，如图8(b)所示。在图8©中，方块表示最佳终端位置，里面的相关数字则是跟踪开放顺序的。我们观察到一个清晰的模式，即前三个终端提供了一个初始的服务布局，后来增加的终端进一步填充了服务区域，其行驶距离相对较大。

为了强调问题的动态性质，我们首先将这种解决方案与静态问题的解决方案进行对比。假设每个地点的需求在时间上是不变的，并且等于整个规划期内的平均值。显然，所有的终端应该同时开放，图8©中的三角形表示静态问题的最佳终端位置。注意只有五个终端被打开，而且终端在空间上的分布更加均匀。当在动态需求下评估时，静态问题的解决方案产生了更高的总成本，即 $4.8×10^5$ 。其次，我们将模型解决方案与一个简单的贪婪启发式解决方案进行对比，在这种情况下，航站楼根据需要开放以满足当前的需求（不考虑未来）。每个新增终端的开放时间由管子模型来估计。图8(d)中的圆圈显示了贪婪的解决方案与动态解决方案（灰色方块）的对比。贪婪的解决方案产生的总成本为 $4.88×10^5$ 。

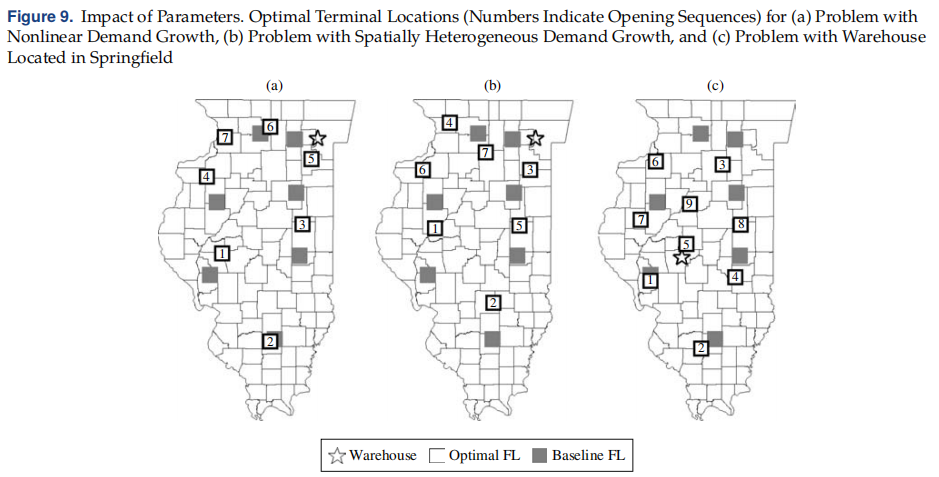
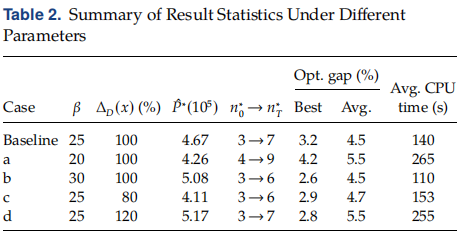
最后，我们评估了成本参数和需求增长率是如何影响最优设计的。结果统计见表2。

5. 总结

本文提出了一个用于解决动态设施位置问题的连续近似框架。首先通过增加时间维度来扩展静态连续设施位置问题。虽然这种转换产生的解决方案没有保持设施位置在时间上的一致性，但它提供了一个可分析的解。随后，我们提出了管子模型，一个圆盘模型的扩展，将CA解决方案转换成离散的设施位置。设施位置的一致性是通过一个迭代的管子调节程序来实现的，即通过一个惩罚方法，其中收敛的解决方案产生了DFLP的近似解决方案。通过一系列的数值例子，我们展示了空间和时间异质性的影响，并比较了CA模型和离散对应模型的性能。我们还将该方法应用于伊利诺伊州的一个经验性案例研究，以探索其在更现实的环境中的适用性。

最后，我们指出，当一组设施在规划期开始时可能已经建成时，可以应用所提出的模型。对于这种情况，可以简单地固定这些位置变量的值。在管子调节程序中，不更新相应管子的中心。这一扩展在设施选址方面提供了很大的实用价值。例如，在系统不确定性程度高或规划范围长的情况下，我们的模型可以在滚动范围内实施。在每个预测周期重新定义（修改）DFLP，以应用所提出的算法，并在不久的将来实施解决方案。然后，到该点开放的设施集成为新问题的固定初始条件，这又可以用上面讨论的程序来处理。

这项研究可以在几个方面进行扩展：（1）研究已开放的设施可以关闭的可能性（市场不一定持续增长）。（2）考虑开放设施可能因为自然或人为的危害而被破坏的情况。