一、线性回归概述
线性回归(Linear regression):是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式
特点:只有一个自变量的情况称为单变量回归,多于一个自变量情况的叫做多元回归
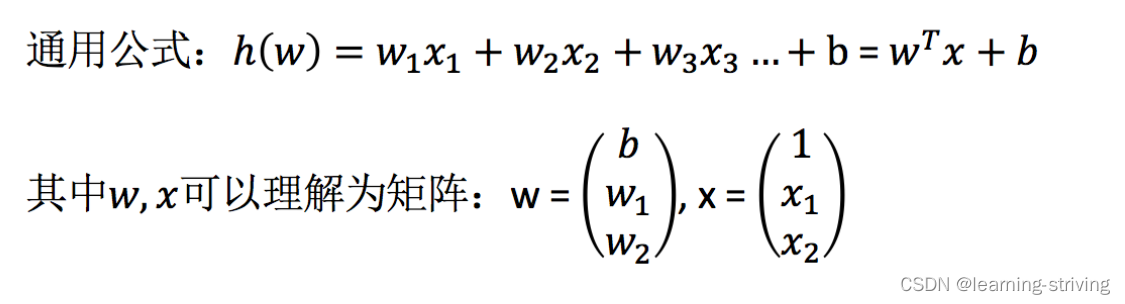
特征值与目标值之间建立了一个关系,这个关系可以理解为线性模型
二、线性回归的特征与目标的关系分析
线性回归当中主要有两种模型,一种是线性关系,另一种是非线性关系。在这里我们只能画一个平面更好去理解,所以都用单个特征或两个特征举例子
线性关系
单变量线性关系与多变量线性关系如下图
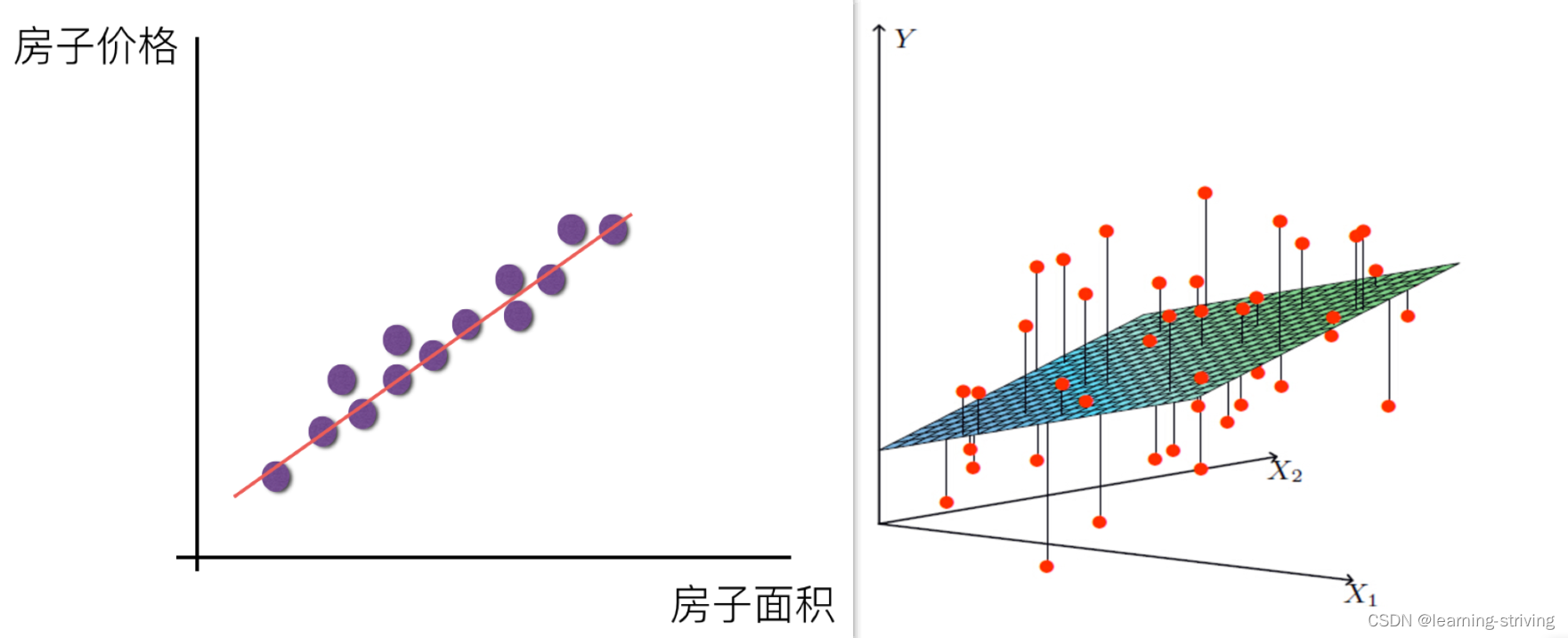
单特征与目标值的关系呈直线关系,或者两个特征与目标值呈现平面的关系
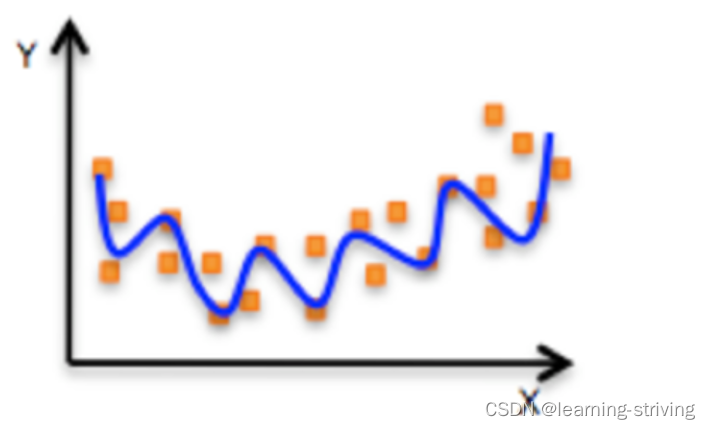
非线性关系回归方程可以理解为:,如下
三、线性回归API
- sklearn.linear_model.LinearRegression()
- LinearRegression.coef_:回归系数
简单使用代码如下
from sklearn.linear_model import LinearRegression
x = [[80, 86], [82, 80], [85, 78], [90, 90], [86, 82], [82, 90], [78, 80], [92, 94]] # [平时成绩,考试成绩]
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4] # 总成绩
estimator = LinearRegression() # 实例化API
estimator.fit(x, y) # 使用fit方法进行训练
print('系数是:', estimator.coef_) # 平时成绩与考试成绩系数,即所占比例
print('预测值是:', estimator.predict([[90, 85]])) # 预测总成绩
------------------------------------------------------------------
输出:
系数是: [0.3 0.7]
预测值是: [86.5]四、常见函数导数

导数的四则运算
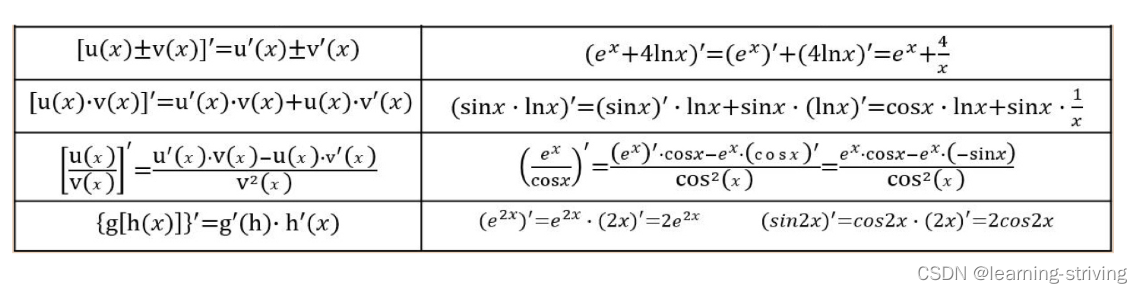
五、损失函数与优化算法
5.1 损失函数
总损失定义为
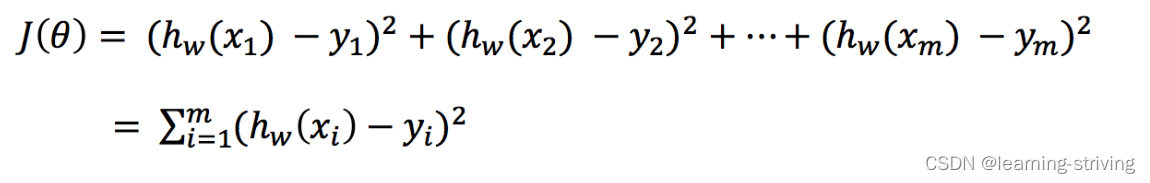
即为各个预测值与真实值之差的平方和,其中
为第i个训练样本的真实值
为第i个训练样本特征值组合预测函数,即预测值
- 损失函数又称最小二乘法
5.2 优化算法(优化减少总损失)
优化的目的:找到最小损失对应的W值
线性回归常用两种优化算法
1.正规方程
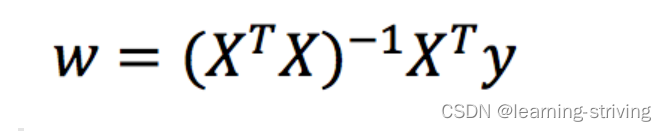
利用矩阵的逆、转置求解,X为特征值矩阵,y为目标值矩阵,将X、y带入后可直接求到最好的结果
缺点:只适合样本和特征较少的情况,当特征过多过复杂时,求解速度太慢并且得不到结果
正规方程的推导过程
把该损失函数转换成矩阵写法
其中y是真实值矩阵,X是特征值矩阵,w是权重矩阵
对其求解关于w的最小值,起止y,X 均已知二次函数直接求导,导数为零的位置,即为最小值
求导推导如下
以上推导过程中, X是一个m行n列的矩阵,并不能保证其有逆矩阵,通过右乘或左乘可将其变成一个方阵,保证其有逆矩阵
2.梯度下降
以下山为例,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷
梯度下降:一个可微分的函数代表一座山,函数的最小值就是山底,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快,因为梯度的方向就是函数之变化最快的方向,重复利用这个方法,反复求取梯度,最后就能到达局部的最小值
- 单变量的函数中:梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
- 多变量函数中:梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
- 梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向
单变量函数梯度下降
假设有一个单变量的函数:J(θ) =
- 函数的微分:J'(θ) = 2θ
- 初始化,起点为:
= 1
- 学习率:α = 0.4
梯度下降的迭代计算过程如下
多变量函数的梯度下降
假设有一个目标函数 :
现在要通过梯度下降法计算这个函数的最小值,通过观察就能发现最小值其实就是 (0,0)点,现从梯度下降算法开始一步步计算到这个最小值,假设初始的起点为: = (1, 3)
初始的学习率为:α = 0.1
函数的梯度为
进行多次迭代
单变量与多变量如图
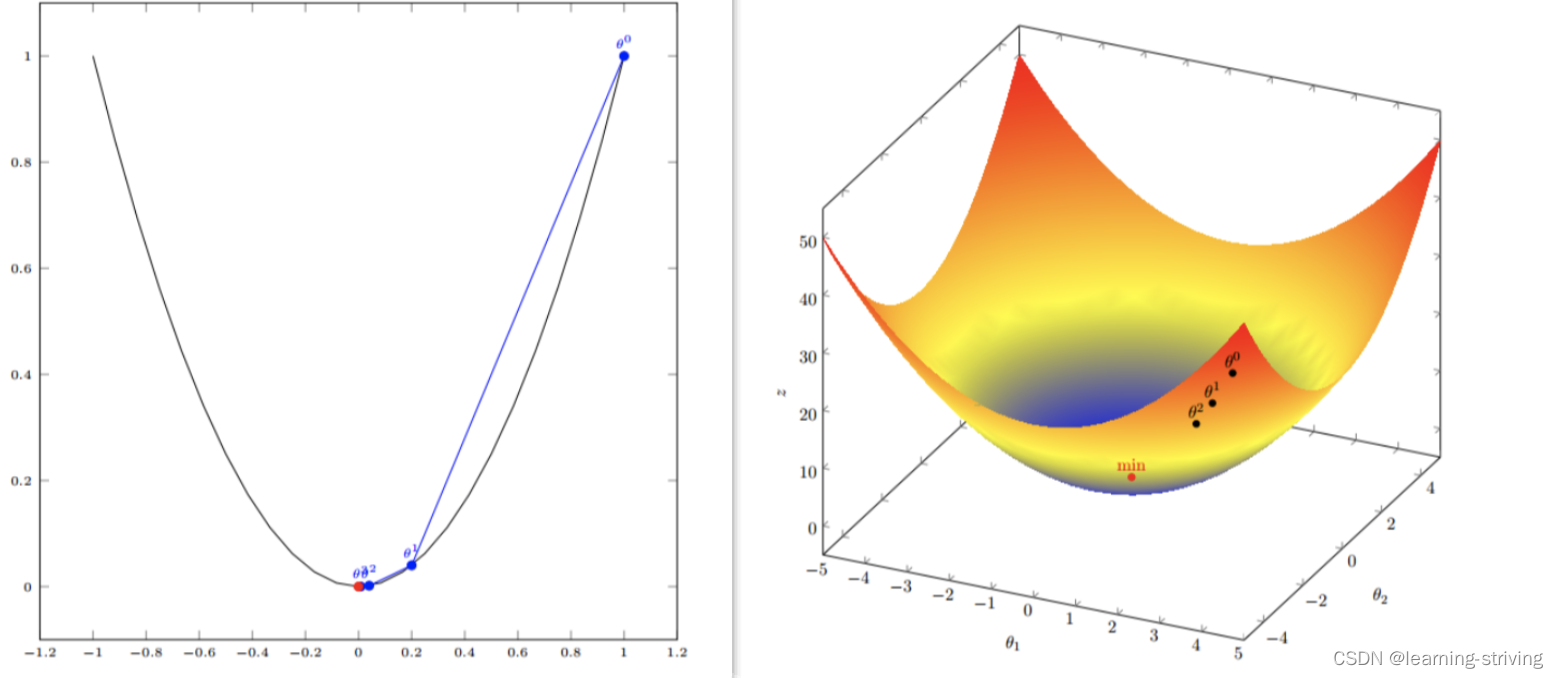
梯度下降(Gradient Descent)公式
α在梯度下降算法中被称作为学习率或者步长,意可以通过α来控制每一步走的距离,以保证不要步子跨的太大,错过了最低点,同时也要保证不要走的太慢
梯度前加一个负号,意味着朝着梯度相反的方向前进,梯度的方向实际就是函数在此点上升最快的方向,朝着下降最快的方向走,自然就是负的梯度的方向,故需要加上负号
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高O( |
有了梯度下降这样一个优化算法,回归就有了"自动学习"的能力
优化动态图如下
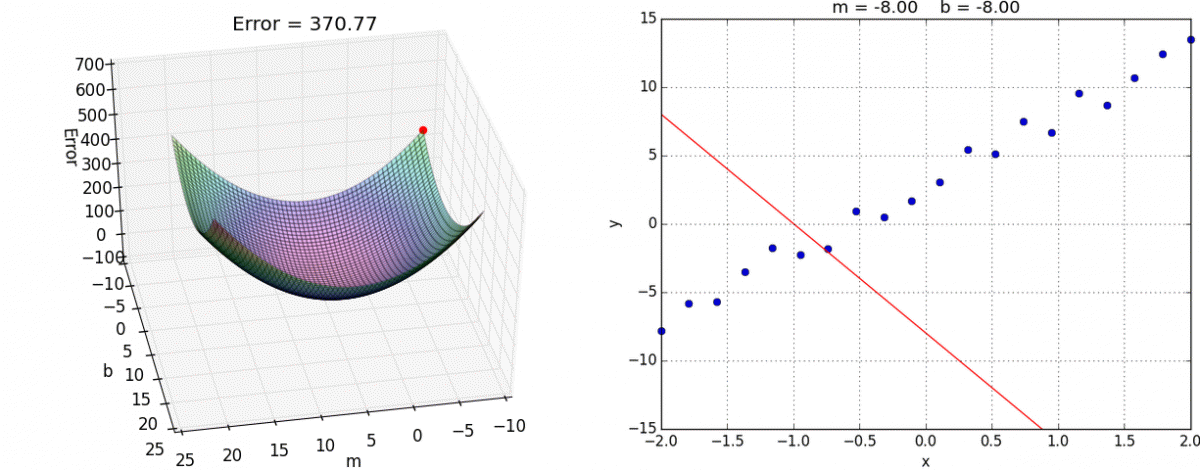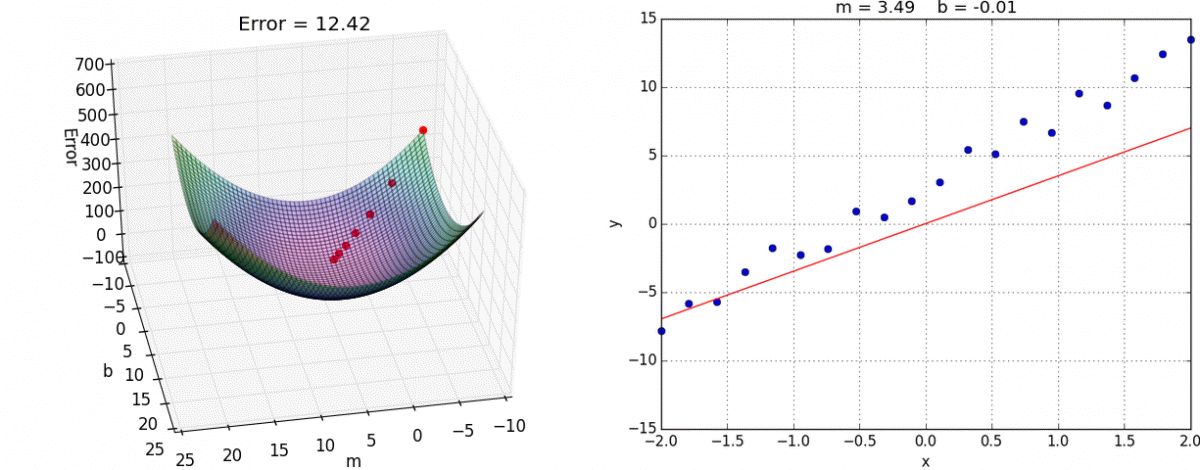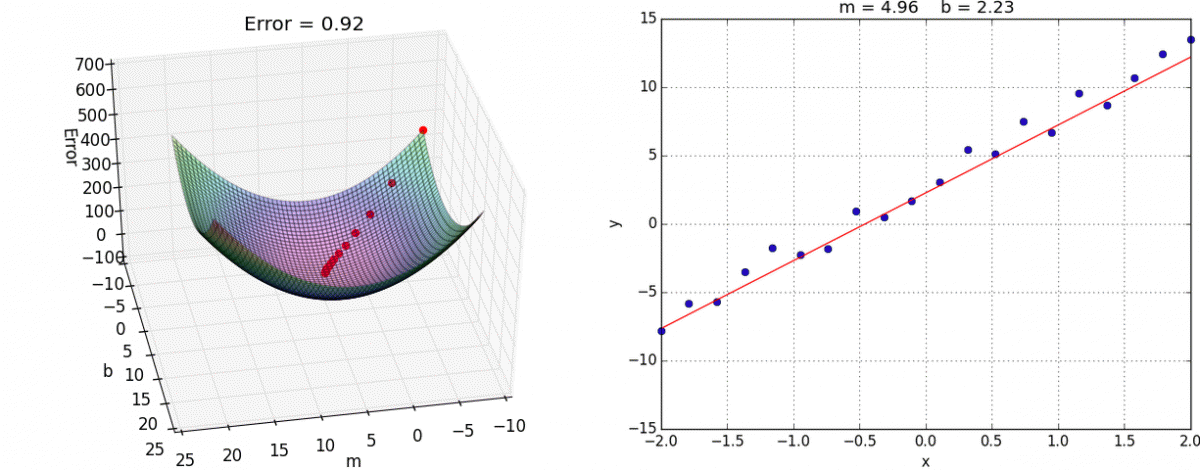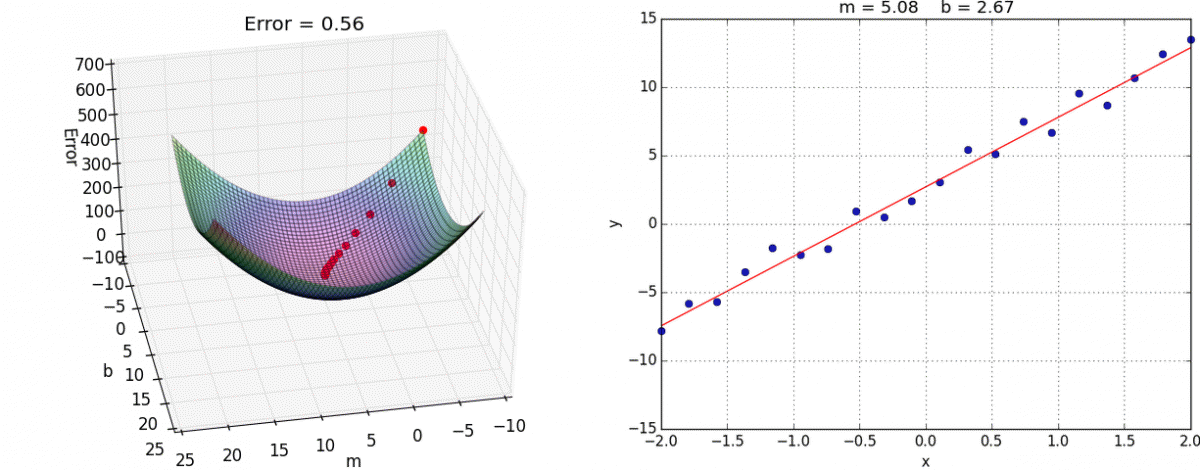
选择
- 小规模数据:LinearRegression(不能解决拟合问题)和岭回归
- 大规模数据:SGDRegressor
学习导航:http://xqnav.top/


![[附源码]JAVA毕业设计微博网站(系统+LW)](https://img-blog.csdnimg.cn/9ab152d6f2344451b071fb45539fa62a.png)