引言

上一节介绍了对比散度(Constractive Divergence)思想，本节将介绍基于含隐变量能量模型的对数似然梯度。

回顾：

包含配分函数的概率分布

在一些基于概率图模型，特别是马尔可夫随机场(无向图) 的基础上，对概率模型分布进行假设：

以马尔可夫随机场(Markov Random Field,MRF)为例，已知随机变量集合 $\mathcal X = \{x_1,x_2,\cdots,x_p\}$ ，它的概率分布 $\mathcal P(\mathcal X)$ 表示如下：
$\mathcal P(\mathcal X) = \frac{1}{\mathcal Z} \sum_{i=1}^{\mathcal K} \psi_i(x_{\mathcal C_i})$
其中 $\psi_i(x_{\mathcal C_i})$ 是描述极大团 $\mathcal C_i$ 内随机变量之间关系信息的势函数(Potential Function)；而 $\mathcal Z$ 表示配分函数(Partition Function)。

实际上， $\psi_i(x_{\mathcal C_i})$ 才是真正描述随机变量关系信息的函数，但它并不是概率分布，需要使用配分函数进行归一化处理，才能得到真正的概率结果。
而受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)在马尔可夫随机场的基础上，针对玻尔兹曼机概率图结构复杂的问题，对结点间的边进行约束。具体约束要求是：观测变量 $v$ ，隐变量 $h$ 的随机变量集合内部无连接，只有 $h$ 和 $v$ 之间存在连接：

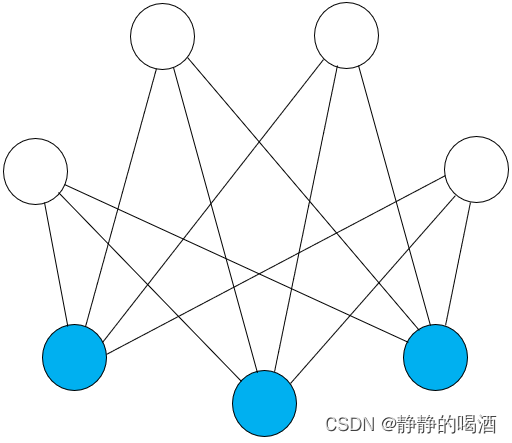
受限玻尔兹曼机——场景构建

基于上图，蓝色结点表示观测变量集合 $v$ ，白色结点表示隐变量集合 $h$ 。为后续计算表达方便，使用向量形式进行表示：
$(h_1,h_2,\cdots,h_m)_{m \times 1}^T \\ v = (v_1,v_2,\cdots,v_n)_{n \times 1}^T$
受限玻尔兹曼机关于随机变量集合 $\mathcal X$ 可表示为如下形式：
$\begin{aligned} & \mathcal P(\mathcal X) = \mathcal P(h,v) \\ & = \frac{1}{\mathcal Z} \exp \{- \mathbb E[h,v]\} \\ & = \frac{1}{\mathcal Z} \exp \left[v^T\mathcal W h + b^T v + c^Th\right] \\ & = \frac{1}{\mathcal Z} \exp \left\{\sum_{j=1}^m \sum_{i=1}^n v_i \cdot w_{ij} \cdot h_j + \sum_{i=1}^n b_iv_i + \sum_{j=1}^m c_j h_j\right\} \\ & s.t.\quad \mathcal Z = \sum_{h,v} \exp \{- \mathbb E[h,v]\} \end{aligned}$
其中模型参数包含如下三个部分：
$\mathcal W = \begin{pmatrix} w_{11},w_{12},\cdots,w_{1n} \\ w_{21},w_{22},\cdots,w_{2n} \\ \vdots \\ w_{m1},w_{m2},\cdots,w_{mn} \end{pmatrix}_{m \times n} \quad b = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}_{n \times 1} \quad c = \begin{pmatrix} c_1\\c_2\\ \vdots \\ c_m \end{pmatrix}_{m \times 1}$

对比散度

在求解包含配分函数概率分布的模型参数过程中，以极大似然估计为例，使用梯度上升法，将最优模型参数 $\hat \theta$ 表述为如下形式：

这里借助蒙特卡洛方法的逆向表述:将样本集合 $\mathcal X = \{x^{(i)}\}_{i=1}^N$ 看作是从‘真实分布’ $\mathcal P_{data}$ 中采集到的样本，在此基础上，将均值结果近似表示为期望形式。
$\frac{1}{N}\sum_{i=1}^N \nabla_{\theta} \log \hat \mathcal P(x^{(i)};\theta) \approx\mathbb E_{\mathcal P_{data}} [\nabla_{\theta} \log \hat \mathcal P(\mathcal X;\theta)]$
关于 $\nabla_{\theta} \log \mathcal Z(\theta)$ 的推导过程详见配分函数——对数似然梯度
$\nabla_{\theta} \log \mathcal Z(\theta) = \mathbb E_{\mathcal P_{model}} \left[\nabla_{\theta} \log \hat \mathcal P(\mathcal X;\theta)\right]$
最终结果可表示为：
$\theta^{(t+1)} \Leftarrow \theta^{(t)} + \eta \nabla_{\theta} \mathcal L(\theta) \\ \begin{aligned} \nabla_{\theta}\mathcal L(\theta) & = \frac{1}{N} \sum_{i=1}^N \left[\nabla_{\theta} \log \hat \mathcal P(x^{(i)};\theta)\right] - \nabla_{\theta} \log \mathcal Z(\theta) \\ & = \mathbb E_{\mathcal P_{data}} \left[\nabla_{\theta} \log \hat \mathcal P(\mathcal X;\theta)\right] - \mathbb E_{\mathcal P_{model}} \left[\nabla_{\theta} \log \hat \mathcal P(\mathcal X;\theta)\right] \end{aligned}$

在对数似然梯度一节中简单提到过，受限玻尔兹曼机是一个典型的正相易求解，负相难求解的模型。通常对负相使用对比散度思想进行求解：
其中 $\mathcal P_0,\mathcal P_{\infty}$ 分别表示 $\mathcal P_{data},\mathcal P_{model}$ ;而 $\mathcal P_k$ 表示第 $k$ 次迭代步骤的吉布斯采样产生的分布，可以将其理解为 $\mathcal P_0,\mathcal P_{\infty}$ 之间某一迭代步骤的‘过渡’。
$\begin{aligned} \hat \theta = \mathop{\arg\min}\limits_{\theta} & \{\mathcal K\mathcal L [\mathcal P_{data} (\mathcal X)\text{ } || \text{ }\mathcal P_{model}(\mathcal X;\theta)]\} \\ & \Downarrow \\ \hat \theta = \mathop{\arg\min}\limits_{\theta} & \left[\mathcal K\mathcal L(\mathcal P_0 \text{ } || \text{ }\mathcal P_{\infty}) - \mathcal K\mathcal L(\mathcal P_k \text{ } || \text{ } \mathcal P_{\infty})\right] \\ \end{aligned}$

基于含隐变量能量模型的对数似然梯度

回顾受限玻尔兹曼机的模型表示(Representation)，它明显是一个无向图模型，它的联合概率分布包含配分函数 $\mathcal Z$ ，这意味着需要对这个 包含配分函数的概率分布进行求解。并且该模型包含隐变量。以该模型为例，介绍包含隐变量能量模型的学习任务。

首先观察似然函数(Log-Likelihood)：
事先定义一个训练集 $\mathcal V = \{v^{(1)},v^{(2)},\cdots,v^{(|\mathcal V|)}\}$ ,实际上指的就是‘观测变量’————样本集合就是可观测的。因而有 $v^{(i)} \in \mathcal R^n(i=1,2,\cdots,|\mathcal V|),n$ 表示观测变量的维度(观测变量v中随机变量的数量)
$\mathcal L(\theta) = \frac{1}{N} \sum_{v^{(i)} \in \mathcal V} \log \mathcal P(v^{(i)};\theta)$
关于 $\mathcal L(\theta)$ 的梯度可表示为：
$\nabla_{\theta}\mathcal L(\theta) = \frac{\partial }{\partial \theta} \left[\frac{1}{N} \sum_{v^{(i)} \in \mathcal V} \log \mathcal P(v^{(i)};\theta)\right]$
将模型表示代入，观察 $\log \mathcal P(v^{(i)};\theta)$ ：
这里仅针对某单个样本,并且模型中存在与其相对应的隐变量 $h^{(i)} \in \mathcal R^m$ .
$\begin{aligned} \log \mathcal P(v^{(i)};\theta) & = \log \left[\sum_{h^{(i)}} \mathcal P(h^{(i)},v^{(i)};\theta)\right] \\ & = \log \left[\sum_{h^{(i)}} \frac{1}{\mathcal Z^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right] \quad \mathcal Z^{(i)} = \sum_{h^{(i)},v^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\} \end{aligned}$
由于 $\frac{1}{\mathcal Z^{(i)}}$ 和 $h^{(i)}$ 之间没有关系(被积分掉了)，因而将其提到 $\sum_{h^{(i)}}$ 前面，表示为如下形式：
再使用 $\mathcal Z^{(i)}$ 的完整形式进行替换。
$\begin{aligned} \log \mathcal P(v^{(i)};\theta) & = \log \left[\frac{1}{\mathcal Z^{(i)}} \sum_{h^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right] \\ & = \log \frac{1}{\mathcal Z^{(i)}} + \log \left[\sum_{h^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right] \\ & = \log \left[\sum_{h^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right] - \log \mathcal Z^{(i)} \\ & = \log \left[\sum_{h^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right] - \log \left[\sum_{h^{(i)},v^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right] \end{aligned}$
至此，对 $\theta$ 求解梯度：
$\begin{aligned} \nabla_{\theta} \left[\log \mathcal P(v^{(i)};\theta)\right] & = \frac{\partial}{\partial \theta} \left[\log \mathcal P(v^{(i)};\theta)\right] \\ & = \frac{\partial}{\partial \theta} \left\{ \log \left[\sum_{h^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right]\right\} - \frac{\partial}{\partial \theta} \left\{\log \left[\sum_{h^{(i)},v^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right]\right\} \\ & = \Delta_1 - \Delta_2 \end{aligned}$

首先观察第一项：
根据‘牛顿-莱布尼兹公式’，将求导符号与连加符号互换。
链式求导法则~将负号提到最前面
$\begin{aligned} \Delta_1& = \frac{\partial}{\partial \theta} \left\{ \log \left[\sum_{h^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right]\right\} \\ & = - \frac{1}{\sum_{h^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}} \sum_{h^{(i)}} \left\{\exp[- \mathbb E(h^{(i)},v^{(i)})] \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} \end{aligned}$
观察前面的分数项：由于 $h^{(i)}$ 被积分掉，因此分数项对于 $h^{(i)}$ 相当于常数。可将该分数项带回积分号内：
负号就留在外面吧~
$\begin{aligned} \Delta_1 = - \sum_{h^{(i)}} \left\{\frac{\exp[- \mathbb E(h^{(i)},v^{(i)})]}{\sum_{h^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}} \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} \end{aligned}$
观察大括号内第一项：将分子分母同乘 $\frac{1}{\mathcal Z^{(i)}}$ ：
并且 $\frac{1}{\mathcal Z^{(i)}}$ 和 $h^{(i)}$ 无关，直接写到 $\sum_{h^{(i)}}$ 内部。
$\begin{aligned} \frac{\frac{1}{\mathcal Z^{(i)}}\exp[- \mathbb E(h^{(i)},v^{(i)})]}{\sum_{h^{(i)}} \frac{1}{\mathcal Z^{(i)}}\exp \{- \mathbb E[h^{(i)},v^{(i)}]\}} = \frac{\mathcal P(h^{(i)},v^{(i)})}{\sum_{h^{(i)}}\mathcal P(h^{(i)},v^{(i)})} = \frac{\mathcal P(h^{(i)},v^{(i)})}{\mathcal P(v^{(i)})} \end{aligned}$
最终，根据条件概率公式，该项就是隐变量 $h^{(i)}$ 的后验概率：
$\frac{\frac{1}{\mathcal Z^{(i)}}\exp[- \mathbb E(h^{(i)},v^{(i)})]}{\sum_{h^{(i)}} \frac{1}{\mathcal Z^{(i)}}\exp \{- \mathbb E[h^{(i)},v^{(i)}]\}} = \mathcal P(h^{(i)} \mid v^{(i)})$
至此， $\Delta_1$ 可表示为：
$\Delta_1 = - \sum_{h^{(i)}} \left\{\mathcal P(h^{(i)} \mid v^{(i)}) \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\}$
同理，继续观察第二项 $\Delta_2$ ：
两项的求解过程非常相似~
$\begin{aligned} \Delta_2 & = \frac{\partial}{\partial \theta}\left\{\log \left[\sum_{h^{(i)},v^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}\right]\right\} \\ & = - \frac{1}{\sum_{h^{(i)},v^{(i)}} \exp \{- \mathbb E[h^{(i)},v^{(i)}]\}} \sum_{h^{(i)},v^{(i)}} \left\{\exp \{- \mathbb E[h^{(i)},v^{(i)}]\} \cdot \frac{\partial}{\partial \theta}\left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} \\ & = -\sum_{h^{(i)},v^{(i)}} \left\{\frac{\exp\{- \mathbb E[h^{(i)},v^{(i)}]\}}{\sum_{h^{(i)},v^{(i)}} \exp\{- \mathbb E[h^{(i)},v^{(i)}]\}} \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} \end{aligned}$
观察大括号内第一项：
$\frac{\exp\{- \mathbb E[h^{(i)},v^{(i)}]\}}{\sum_{h^{(i)},v^{(i)}} \exp\{- \mathbb E[h^{(i)},v^{(i)}]\}} = \frac{1}{\mathcal Z}\exp\{- \mathbb E[h^{(i)},v^{(i)}]\} = \mathcal P(h^{(i)},v^{(i)})$
由于分母将 $h^{(i)},v^{(i)}$ 全部积分掉了，因而分母就是配分函数 $\mathcal Z$ ，该分数项就是联合概率分布 $\mathcal P(h^{(i)},v^{(i)})$ 。

至此， $\Delta_2$ 可表示为：
$\Delta_2 = -\sum_{h^{(i)},v^{(i)}} \left\{\mathcal P(h^{(i)},v^{(i)}) \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\}$

最终，关于能量函数给定观测变量(单个样本 $v^{(i)}$ )条件下，对数似然梯度可表示为：
$\begin{aligned} \nabla_{\theta} \left[\log \mathcal P(v^{(i)};\theta)\right] & = \Delta_1 - \Delta_2 \\ & = \sum_{h^{(i)},v^{(i)}} \left\{\mathcal P(h^{(i)},v^{(i)}) \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} - \sum_{h^{(i)}} \left\{\mathcal P(h^{(i)} \mid v^{(i)}) \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} \end{aligned}$

最终，根据牛顿-莱布尼兹公式，关于 $\mathcal L(\theta)$ 梯度可表示为：
$\begin{aligned} \nabla_{\theta} \mathcal L(\theta) & = \frac{\partial }{\partial \theta} \left[\frac{1}{N} \sum_{v^{(i)} \in \mathcal V} \log \mathcal P(v^{(i)};\theta)\right] \\ & = \frac{1}{N} \sum_{v^{(i)} \in \mathcal V} \nabla_{\theta}\left[\log \mathcal P(v^{(i)};\theta)\right] \end{aligned}$