化简原理
等价状态:
1、必要条件:在同样的输入作用下,有相同的输出
2、同样的输入条件下,相应的次态彼此等价
等价次态:
1、对应的次态相同
2、次态为两个现态本身或交错
3、两个次态为状态对封闭链中的一对
4、两个次态的某一后续状态对可以合并
等价状态具有可传递性:AB 等价,AC 等价= >BC 等价,则 A、B、C 为等价类
等价类:彼此等价的状态的集合
最大等价类:一个等价类不包含在任何其他等价类中
化简原始状态表= > 寻找最大等价类
但其实,化简原理应该不是很重要,主要是要求你会化简的方法
K次划分法
先找出输出相同的状态集合,为一次划分,再找第二次输入下输出也相同的集合,依此类推,直到 k + 1 次不能再划分,找到最大等价类集合。
步骤:
- 找出输出相同的状态集合进行划分。
- 将次态所在的集合做为下标,更新在集合中。
- 若下标不同,则拆分等价状态类。
- 直到所有的下标都保持一致。
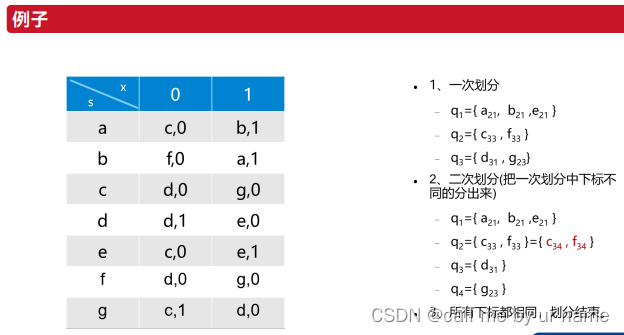
as for q1:a,b,c的输出都是0,1,所以放一起
for 下标:a的次态是c和b,而c在q2中,b是在q1中的,所以下标是21
至于q3,d31和g23下标不一样,所以要拆开
拆开完之后需要对前面的元素的下标重新编
隐含表法
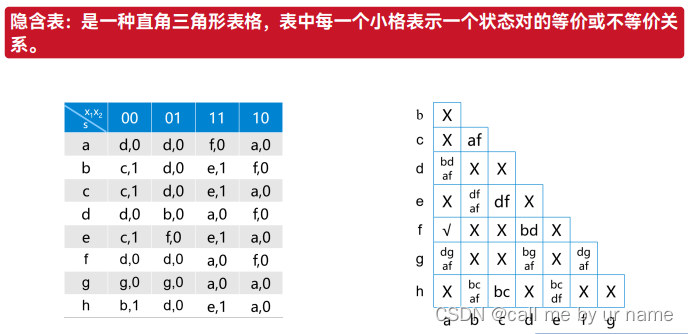
行数里去掉一个a(首),列数里去掉一个h(尾)


- 构作隐含表,分情况讨论:A 等价 √ B 不等价 × C 条件
- 顺序比较追踪,找出所有等价状态
- 形成最大等价类集合
- 构成最简状态表
次佳编码法
确定需要几位二进制码 k [log2 N] 向上取整简而言之——3个状态要2位二进制,8个状态要3位二进制
编码规则
- 次态相同,现态相邻
- 现态相同,次态相邻
- 输出相同,现态相邻
- 优先顺序 1>2>3

在x=0时,a和b的次态相同;在x=1时,a和c的状态相同
所以a,b的编码要相邻;a,c的编码要相邻
用 JK 触发器及与非门设计一个同步二进制串行加法器例
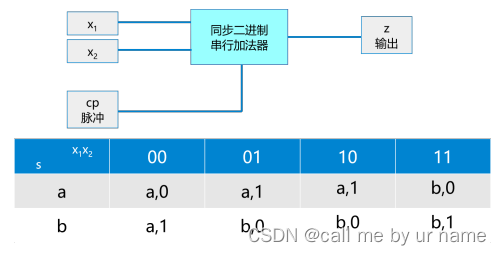
- 确定输入、输出。建立原始状态表
- 化简并建立最简状态表
- 状态编码
- 建立控制、输出函数表达式
- 画电路图
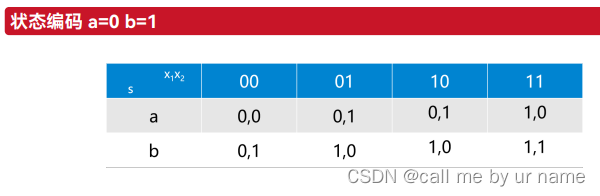
这题只有1位二进制,不是很能验证上文的编码规则
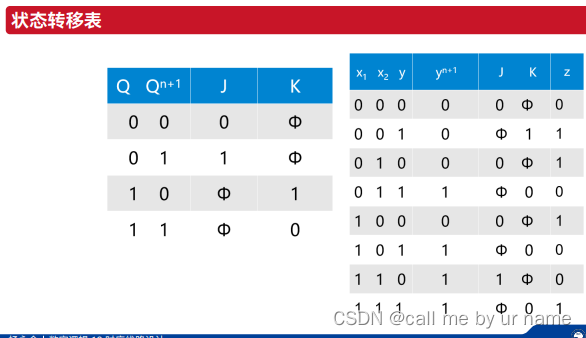

作业
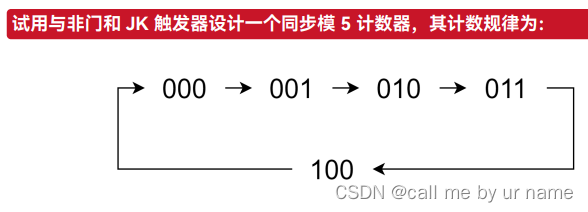
- 确定输入、输出。建立原始状态表
- 化简并建立最简状态表
- 状态编码
- 建立控制、输出函数表达式
- 画电路图


![[附源码]Python计算机毕业设计Django在线教育系统](https://img-blog.csdnimg.cn/d9d8c81e2a1b4367b2e5d03d343be793.png)