递归算法是一种直接或间接调用原算法的算法，一个使用函数自身给出定义的函数被称为递归函数。利用递归算法可以将规模庞大的问题拆分成规模较小的问题，从而使问题简化。无论是递归算法还是递归函数，最大的特点都是“自己调用自己”。

斐波那契数列

斐波那契数列的规律是：第一项是1，第二项是1，以后每一项都等于前两项之和。我们的问题是：斐波那契数列的第n项是多少？

$F(n)=\begin{cases} 1\quad n=1\\ 1\quad n=2\\ F(n-1)+F(n-2)\quad n\geq3 \end{cases}$
在计算斐波那契数列的第n项F(n)时，首先需要得到F(n-1)和F(n-2)的值，而F(n-1)和F(n-2)也可以通过这个公式计算，所以斐波那契数列具有递归特性，可以使用递归算法计算出数列第n项的值。

#include<iostream>

int fibonacci(int n) {
	if (n == 1 || n == 2) {
		return 1;
	}
	else {
		return fibonacci(n - 1) + fibonacci(n - 2);
	}
}
int main() {
	//检验结果
	std::cout << fibonacci(10);
}

在使用递归算法的时候需要注意：

每个递归函数都必须有一个非递归定义的初始值作为递归结束标志。就像上述fibonacci()函数，当n==1||n==2时函数返回1，不再调用自己。如果一个递归函数中没有定义非递归的初始值，那么该递归调用是无法结束的，也就得不到结果。
递归算法解决的问题需要具有递归特性，就像上述fibonacci()函数，fibonacci(n)的值可以通过fibonacci(n-1)和fibonacci(n-2)的值相加得到，其本质就是一种反复调用自身的过程。
虽然通过递归算法结构简单，已于理解和实现，但是由于需要反复调用自身，所以运行效率较低，时间复杂度和空间复杂度较高，在使用时应考虑效率和性能问题。

数组的全排列

编写一个程序，将数组中的元素进行全排列，并输出每一种排列方式。例如数组中的元素为{1,3,5}，那么程序可以输出该数组元素的6种排列方式，分别为{1,3,5},{1,5,3},{3,1,5},{3,5,1},{5,1,3},{5,3,1}。

解决数组全排列问题最经典的方法是递归算法，因为数组的全排列问题具有很明显的递归特性。可以将数组全排列问题形式化定义为以下模型：
设数组 $R$ 包含 $n$ 个元素，定义符号 $R_i=R-{r_i}$ ， $R_i$ 表示原数组 $R$ 去掉元素 $r_i$ 后的新数组。数组 $R$ 的全排列 $P er m (R)$ 可定义如下：

当n==1时， $Perm(R)=\{r\}$ ，其中 $r$ 为数组 $R$ 中的唯一元素。
当n>1时， $P er m (R)$ 由全排列 $r_1)Perm(R_1)$ , $r_2)Perm(R_2)$ , $r_n)Perm(R_n)$ 构成。

很显然，上面全排列的定义具有递归特性，依此递归定义可以设计出如下递归算法：

void perm(vector<int> vec, vector<int> tmpResult, vector<vector<int>>& result) {
	if (vec.size() == 1) {
		tmpResult.push_back(vec[0]);
		result.push_back(tmpResult);
	}
	else {
		for (int i = 0; i < vec.size(); i++) {
			tmpResult.push_back(vec[i]);
			vec.erase(vec.begin() + i);
			perm(vec, tmpResult, result);
			vec.insert(vec.begin() + i, tmpResult.back());
			//恢复到迭代前的状态
			tmpResult.pop_back();
		}
	}
}

第一个if语句即是递归的结束条件，当待排序数组只剩一个元素时，直接插入到临时结果数组中，然后将临时结果添加到结果数组中。
如果不满足if语句，则说明需要继续排列。使用循环取出当前数组的每一个元素，添加到临时结果数组中：

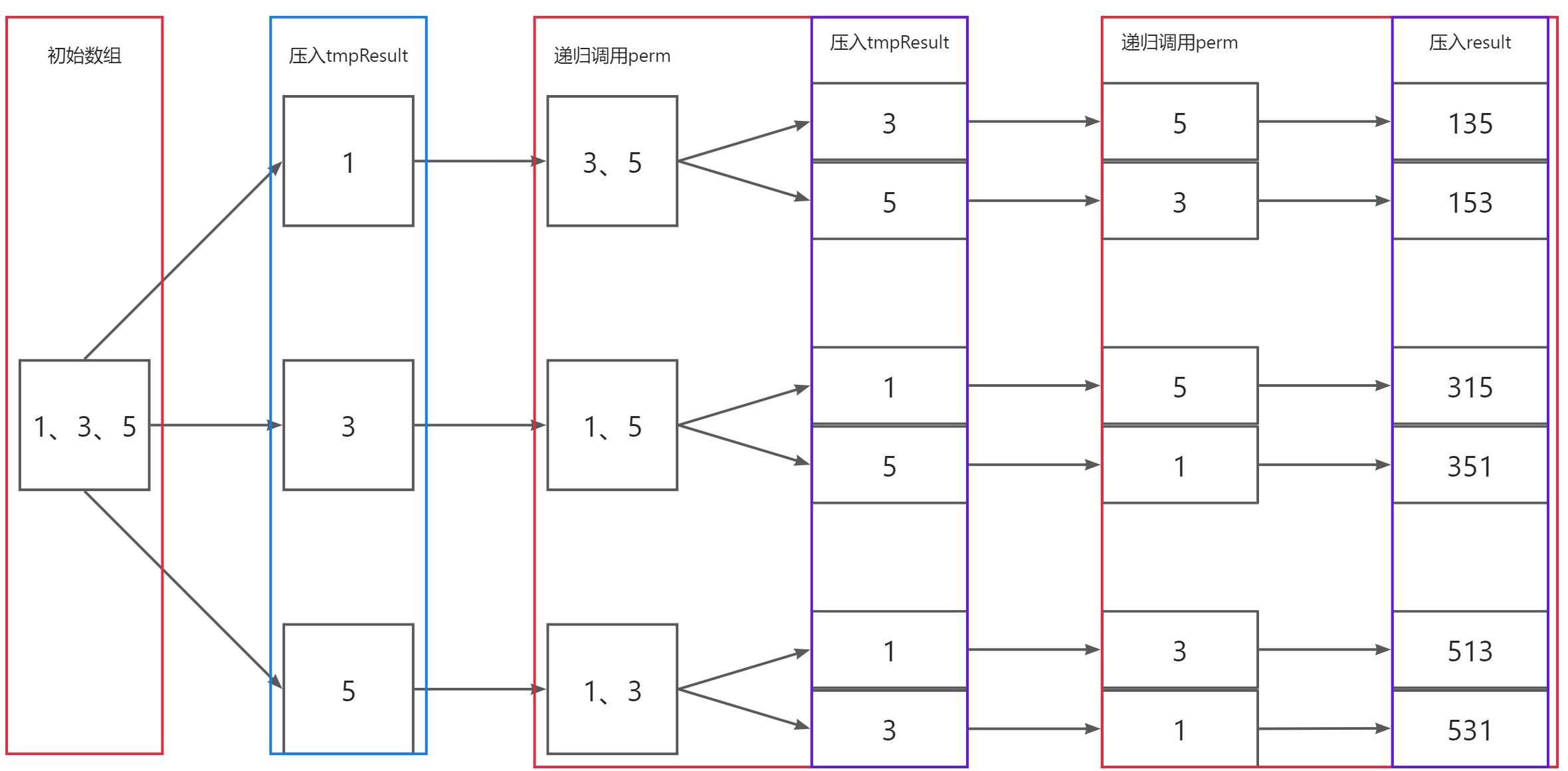
每次递归调用只修改原数组中的一个数据，在调用完perm()后需要将数组恢复到迭代前的状态。
上面的代码易于理解，但使用了至少三个vector容器，空间复杂度较高。
理解原理和代码之后，我们就可以做出简化，通过调整指针位置，使用纯数组进行解决：

#include<stdio.h>
void swap(int* a, int* b) {
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
//数组指针，开始下标，结束下标
void permutation(int* arr, int start, int end) {
	if (start == end) {
		for (int i = 0; i <= end; i++) {
			printf("%d ", arr[i]);
		}
		puts("");
	}
	else {
		for (int i = start; i <= end; i++) {
			//交换起始元素和当前元素
			swap(arr + start, arr + i);
			//递归生成后续元素的排列
			permutation(arr, start + 1, end);
			//恢复到迭代前的状态
			swap(arr + start, arr + i);
		}
	}
}
int main() {
	int a[] = { 1,3,5,7 };
	permutation(a, 0, 3);
	return 0;
}

这种算法的本质还是将数组的每个元素取出压入结果数组，对剩余元素重复“取出-压入-重复”的操作。
结果数组与原数组共用内存空间，通过指针位置调整边界。
如果文件后缀名为.cpp，则默认使用C++编译器，不能在函数内使用sizeof(arr)/sizeof(arr[0])的方法获取数组大小，sizeof(arr)得到的是指针大小。此时，函数参数中的end不能省略。
如果使用C++的方法实现全排列，除了上面两种方法，还可以使用C++封装好的标准库函数next_permutation。

#include<iostream>
#include<vector>
#include<algorithm>
int main() {
	std::vector<int> vec = { 1,3,5 };
	do {
		for (auto it = vec.begin(); it != vec.end(); it++) {
			std::cout << *it << " ";
		}
		std::cout << std::endl;
	} while (std::next_permutation(vec.begin(), vec.end()));
	return 0;
}

使用标准库有以下几个需要注意的地方：

next_permutation在algorithm头文件下，使用时需要包含此头文件，已及所使用的STL头文件。
通常使用do...while结构，如果直接使用while，循环代码块内会丢失默认的排序情况。
无论循环代码块内执行什么操作，退出循环之后，容器会恢复到进入循环之前的状态。

梵塔问题

有三根杆子A，B，C。A杆上有 N 个 (N>1) 穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 C 杆：

每次只能移动一个圆盘；
大盘不能叠在小盘上面。

提示：可将圆盘临时置于 B 杆，也可将从 A 杆移出的圆盘重新移回 A 杆，但都必须遵循上述两条规则。
问：如何移？最少要移动多少次？

题目分析

梵塔问题只能用递归算法来解决。我们可以考虑移动的步骤：

将A针上的N-1个圆盘借助C针移动到B针上。
将A底部的圆盘移到C针上。
将B针上的N-1个圆盘借助A针移动到C针上。

完成这三步就可以将A针上的64个圆盘全部移到C针上，而且在移动过程中始终保持大盘在下小盘在上的顺序。关键在于第1步和第3步如何执行。

这显然成为一个新的梵塔问题，只不过这个梵塔问题的规模要小一些，从N个盘子变成N-1个盘子：

将A针上的N-1个盘子借助C针移到B针上。
将B针上的N-1个盘子借助A针移到C针上。

问题1的解决步骤如下：

将A针上的N-1-1个圆盘借助B针移动到C针上。
将A底部的倒数第二个圆盘移到C针上。
将C针上的N-1-1个圆盘借助A针移动到B针上。

问题2的解决步骤如下：

将B针上的N-1-1个圆盘借助C针移动到A针上。
将B底部的倒数第二个圆盘移到C针上。
将A针上的N-1-1个圆盘借助B针移动到C针上。

上述问题1和问题2的解决步骤中，第1步和第3步又构成了两个新的梵塔问题，只是问题的规模又缩小了一些，从N-1个盘子缩小到N-2个盘子。
这两个问题的解决方案与上面一样，仍然分三步移动圆盘不断将问题的规模缩小，直到第1步和第3步移动的盘子个数为1。这显然是一个递归问题，也就是梵塔问题中嵌套着更小规模的梵塔问题。

#include<iostream>
//要移动的盘子数量，从from借助by移动到to
void move(int n, char from, char by, char to) {
	if (n == 1) {
		std::cout << from << " to " << to<<std::endl;
	}
	else {
		//第一步，将A针上的n-1个盘子借助C针移动到B上
		move(n - 1, from, to, by);
		//第二步，将A针底部的盘子移动到C上
		std::cout<< from << " to " << to << std::endl;
		//第三步，将B针上的n-1个盘子借助A针移动到C上
		move(n - 1, by, from, to);
	}
}
int main() {
	move(3, 'A', 'B', 'C');
	return 0;
}

该函数是一个递归函数，递归结束的条件是n==1，此时只需要移动一个圆盘，无需借助by针，可以直接从from针上移到to针上。如果n!=1，则要将问题继续分解，也就是递归地调用函数move()。按照之前分析的步骤，先将A针上的N-1个圆盘借助C针移动到B针上，然后将A底部的圆盘移到C针上，最后将B针上的N-1个圆盘借助A针移动到C针上。
对于N个盘子，需要移动 $2^n-1$ 次，因此上面的代码中只模拟了3个盘子的情况。