一、实验目标

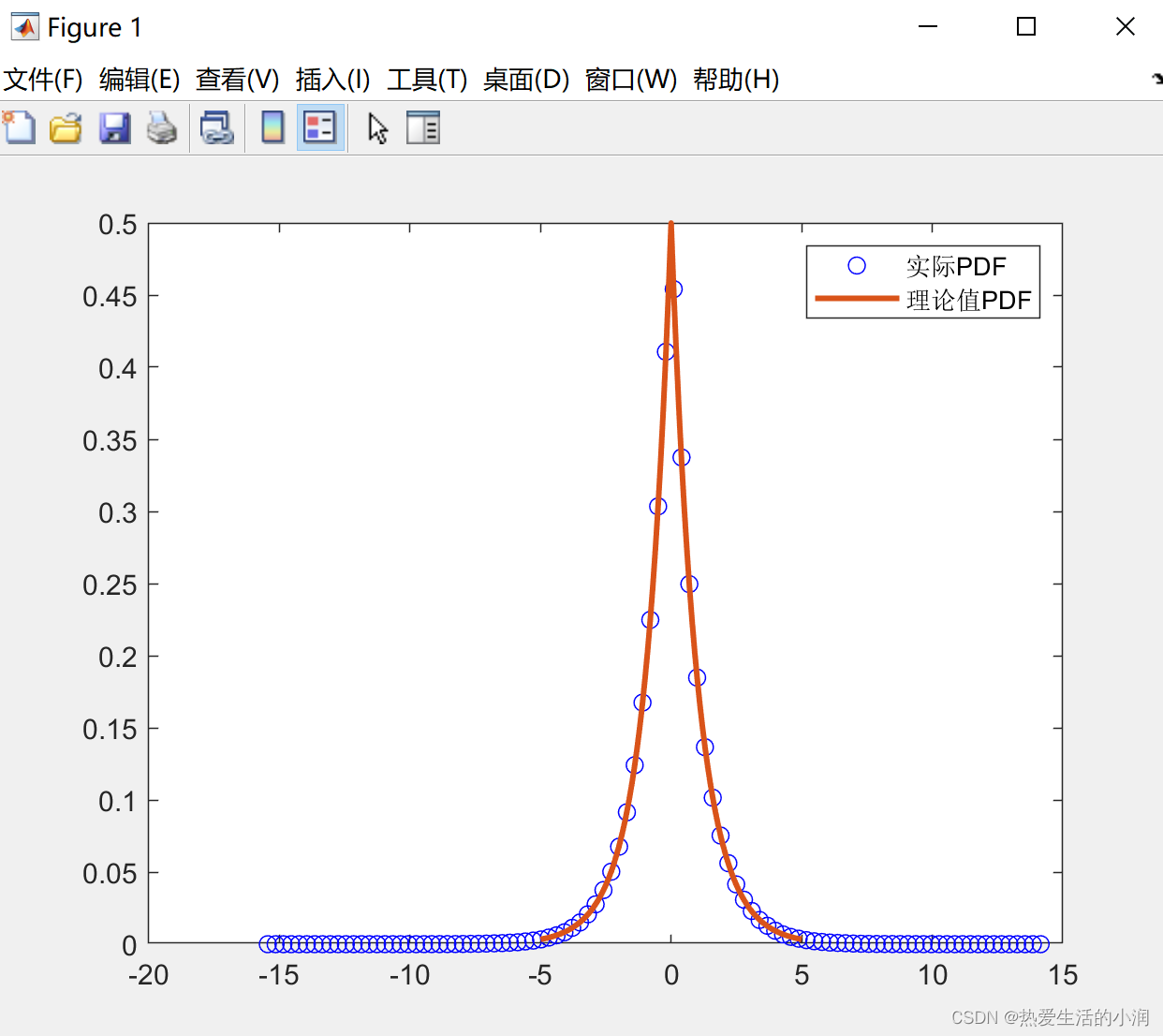
生成拉普拉斯分布的噪声，并分析它的概率密度函数

二、解决思路

（1）拉普拉斯分布可以由指数分布生成

拉普拉斯的概率密度函数为
$f(x;\mu,\lambda)=\frac{1}{2 \lambda} e^{-\frac{|x-\mu|}{\lambda}}$
而指数分布的概率密度函数为
$\begin{gathered} f(x)=\lambda e^{-\lambda x}, x>0 \\ f(x)=0, x \leq 0 \end{gathered}$
由上可知，当 $\mu = 0$ 时，拉普拉斯分布的正半部分是尺度参数为 $1/\lambda$ 的指数分布的一半。
且拉普拉斯分布的概率密度函数是左右对称的，由此可以通过指数分布生成拉普拉斯分布。
（2）使用ksdensity函数估计生成的拉普拉斯变量的概率密度函数

三、实验代码

主函数：main.m

close all;clc;clear all;

%% 参数设置
length = 5000000;
lambda = 1;

%% 生成噪声
y = randlap(length,lambda); % 生成拉普拉斯噪声

%% 概率密度计算

% 估计概率密度
[yy,x]=ksdensity(y);

% 计算概率密度理论值
xx = transpose(-5:1e-1:5);
miu = 0;
probablity = 1 / ( 2*lambda ) * exp( -abs(xx-miu) / lambda );

%% 作图
figure;xlabel('x');ylabel('PDF');
plot (x,yy,'bo'); % 做概率分布折线图
hold on;
plot (xx,probablity,'LineWidth',2);
legend('实际PDF','理论值PDF');

子函数：randlap.m

function x = randlap(siz,lambda)

% lambda就是lambda，siz是维度，这里默认miu是0

% RANDL  random numbers distributed according to the Laplace distribution
%   RANDL(N) will return an NxN matrix containing pseudo-random values
%   drawn from a Laplace distribution with zero mean and standard deviation
%   one. RAND([M,N,...,P]) will return an MxNx...xP matrix.
%   RANDL([M,N,...,P],lambda) will return an MxNx...xP matrix of
%   pseudo-random numbers with parameter lambda. CAUTION: the pdf is
%   assumed as 
%           pdf = lambda/2 * exp(-lambda*abs(x))
%
% The Laplace random numbers are generated using the the RAND function to
% generate uniformly distributed numbers in (0,1) and then the probability
% integral transformation, i.e. using the fact that 
%   if Fx(x) is the cdf of a random variable x, then the RV z=Fx(x) is
%   uniformly distributed in (0,1).
%
% In order to generate random numbers with mean mu and variance v, then
% generate the random numbers X with mean 0 and variance 1 and then
%       X = X*sqrt(v)+mu;
%
% C. Saragiotis, Oct 2008

% 23-07-03 大概明白的，就是用了一个指数分布的形式去生成的


if nargin==1
    lambda = sqrt(2); % this gives a std=var=1.
end

% z = rand(siz);
% x = zeros(siz);

% 23-07-03 改为
z = rand(siz,1);
x = zeros(siz,1);

in = z<=.5;
ip = z> .5;
x(in) =  1/lambda *log(2*z(in));
x(ip) = -1/lambda *log(2*(1-z(ip)));