引言
线性回归是一种最简单、也是最常用的预测模型,主要用于处理自变量和因变量之间的线性关系。举个例子,假设你是一名大学生,正在为你的经济学课程做一个研究项目,你想要知道大学生的学习时间和GPA(绩点平均分)之间的关系。在这个情况下,线性回归就可以派上用场。你可以收集一些数据,例如你的同学们的学习时间和GPA,然后用线性回归模型去拟合这些数据,看看学习时间是否对GPA有显著的影响,以及影响的程度如何。
虽然线性回归是个基础模型,但是你会惊奇地发现,其实它在许多领域都有着广泛的应用。例如在经济学中,我们可以用它来预测消费者支出;在医学领域,我们可以用它来分析风险因素对疾病发生的影响;在商业领域,我们可以用它来预测销售额等等。总的来说,只要你希望从一些数据中找出规律,预测未来,线性回归都可能是你的得力助手。
接下来的文章,我们将首先探讨线性回归的理论基础,然后我们会使用Python的sklearn库来进行实战操作。最后,我们还会以房价预测为例,让你看到线性回归在实际问题中的运用。
线性回归的理论基础
在我们开始实战线性回归模型之前,让我们先了解一下其背后的理论知识。
线性回归是一个用来预测连续型目标变量的模型。其数学公式表达如下:y = β0 + β1*x1 + β2*x2 + ... + βn*xn + ε,其中y代表目标变量,x1, x2, ..., xn是自变量,β0, β1, ..., βn是模型参数,ε是误差项。在这个公式中,β0被称为截距项,表示当所有自变量都为0时,预测的y值;β1, ..., βn是斜率参数,描述了每个自变量对目标变量的影响程度;误差项ε表示模型未能解释的部分。
接下来,我们来看看什么是损失函数,以及为什么我们要最小化它。在线性回归中,我们通常使用均方误差(Mean Squared Error, MSE)作为损失函数,其公式如下:MSE = 1/n * Σ(yi - (β0 + β1*xi))^2,其中n是样本数量,yi和xi分别是第i个样本的目标值和自变量值。损失函数度量了我们的模型预测值和真实值之间的差距。我们的目标是通过调整模型参数β0, β1, ..., βn来最小化损失函数,使得模型的预测值尽可能接近真实值。
那么,如何调整模型参数以最小化损失函数呢?这就需要用到一个叫做梯度下降的优化算法。梯度下降的思想是,先随机初始化模型参数,然后计算损失函数在当前参数下的梯度(即损失函数对每个参数的偏导数),然后将模型参数沿着梯度的负方向更新一小步,这样就可以使损失函数的值下降。重复这个过程,直到损失函数的值不再显著下降,我们就找到了一组可以使损失函数最小化的模型参数。
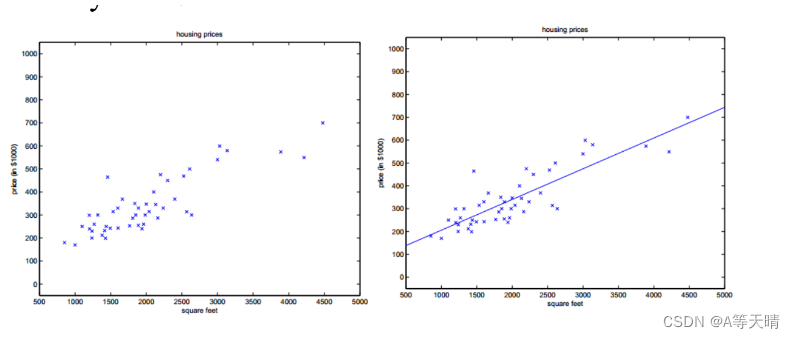
让我们以一个简单的例子来说明这个过程。假设我们有一个单变量线性回归问题,即我们只有一个自变量x。我们的模型就变成了y = β0 + β1*x + ε。我们的目标是找到一组β0和β1的值,使得我们的模型可以很好地拟合数据。通过梯度下降,我们可以逐步调整
β0和β1的值,使得损失函数(即模型预测值和真实值之间的均方差)最小化。
以房价预测为例,假设我们已经收集了一些房屋面积(x)和对应的售价(y)的数据。我们可以初始化β0和β1为任意值,然后计算在这个参数下的损失函数值。然后,我们计算损失函数对β0和β1的偏导数,也就是梯度。假设我们计算出来的梯度为g0和g1,那么我们就可以将β0和β1分别更新为β0 - α*g0和β1 - α*g1,其中α是学习率,是一个正的小数。这样,我们就完成了一次参数更新。
然后我们再计算新的损失函数值,如果它比之前小了,那么说明我们的参数更新是有效的。我们就可以继续这个过程,直到损失函数的值不再显著下降,或者达到预设的最大迭代次数。
通过这个过程,我们就找到了一组可以使损失函数最小化的β0和β1的值。这就是我们的线性回归模型。然后,我们就可以使用这个模型来预测新的房屋的售价。例如,如果有一个新的房屋,我们知道它的面积是x',那么我们就可以预测它的售价为β0 + β1*x'。
以上就是线性回归的理论基础和工作原理。理解了这些,你就已经迈出了成为一个数据科学家的第一步!接下来,我们将在Python中实现这个过程,让理论转化为实践。
线性回归的实践
理解了线性回归的理论之后,我们来看看如何在实践中应用它。我们将会走过数据预处理、模型的创建和训练,以及模型评估这几个重要步骤。
首先是数据预处理。在现实中的数据往往是“脏”的,也就是说,它们可能包含缺失值,有异常值,或者特征的量纲不一致等问题。对于缺失值,我们可以选择删除含有缺失值的样本,或者用某种方法进行填充。例如,我们可以用该特征的均值或中位数来填充缺失值。特征缩放是另一个常见的数据预处理步骤,它可以使得所有特征都在同一数量级上,从而避免某些特征因为量纲大而对模型产生过大的影响。最常用的特征缩放方法是标准化,即将特征值减去其均值,然后除以其标准差,得到的新特征值都符合标准正态分布。
接下来是模型的创建和训练。Python的sklearn库为我们提供了一个方便的接口来创建和训练线性回归模型。以下是一段创建和训练线性回归模型的示例代码:
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 假设X为特征数据,y为目标变量
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
model = LinearRegression()
model.fit(X_train, y_train)
最后是模型的评估。线性回归模型的常见评估指标包括决定系数R^2和均方误差(MSE)。决定系数R^2表示模型可以解释的数据变动的比例,其值越接近1,说明模型的预测能力越好。均方误差MSE是预测值与真实值之间差的平方的均值,其值越小,说明模型的预测能力越好。在sklearn中,我们可以使用以下代码来计算这两个指标:
from sklearn.metrics import r2_score, mean_squared_error
y_pred = model.predict(X_test)
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print('R^2:', r2)
print('MSE:', mse)
以上就是线性回归在实践中的应用。在后续的文章中,我们会更深入地探索这个主题,包括如何对线性回归模型进行改进,如何处理更复杂的数据等问题。在你掌握了这些基础之后,你将会发现,线性回归并不是一个简单的工具,而是一把强大的“瑞士军刀”。它可以帮助我们解决各种各样的预测问题,只需要我们对数据和问题有足够深入的理解,以及灵活的应用方法。
例如,线性回归模型虽然是一个线性模型,但是我们可以通过引入非线性特征(如原始特征的平方项、立方项等)或者交互项(不同特征相乘)来拓展它的能力,使其可以拟合非线性的数据关系。同样,我们还可以通过正则化的方法(如L1正则化、L2正则化等)来控制模型的复杂度,防止模型过拟合,从而提高模型的泛化能力。
所以,尽管线性回归看起来很简单,但是如果你能深入理解它并灵活应用,它绝对是你数据科学家工具箱中的一把利器。希望你在学习和探索线性回归的过程中能够感受到它的魅力,也希望你能将它成功应用在你的研究或工作中。
实战案例:房价预测
在理论知识和基本操作的熟悉后,让我们把这些知识应用到一个实际的例子中去。我们的目标是预测房价,一个经典而实用的案例。假设我们手头有一个包含各种房屋特征(例如面积、卧室数量、地理位置等)以及对应房价的数据集,我们希望通过这个数据集来建立一个模型,以预测未知的房屋的价格。
首先,我们需要读取和分析数据。假设我们的数据存储在一个CSV文件中,我们可以使用Python的pandas库来读取和处理这个数据:
import pandas as pd
# 读取数据
data = pd.read_csv('house_price.csv')
# 查看数据的前几行
print(data.head())
# 数据描述性统计
print(data.describe())
在数据分析阶段,我们可以利用数据的描述性统计(例如均值、中位数、最小值、最大值等)以及可视化(例如直方图、箱线图等)来了解数据的分布和关系。
接下来,我们需要创建并训练线性回归模型。这一步我们已经在前面的章节中介绍过,我们可以将数据分为训练集和测试集,然后用训练集数据训练模型,用测试集数据测试模型的性能:
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# 假设X是特征数据,y是目标变量
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 创建模型
model = LinearRegression()
# 训练模型
model.fit(X_train, y_train)
# 预测测试集数据
y_pred = model.predict(X_test)
模型训练好之后,我们就可以用一些指标来评估模型的性能,例如R^2,均方误差(MSE)等:
from sklearn.metrics import r2_score, mean_squared_error
# 计算R^2和MSE
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print('R^2:', r2)
print('MSE:', mse)
最后,我们需要解读模型参数,以及进行模型结果的业务解读。例如,线性回归模型的参数β可以告诉我们特征与目标变量之间的关系。如果β为正,那么特征值的增大会导致目标变量的增大;如果β为负,那么特征值的增大会导致目标变量的减小。此外,β的绝对值大小还可以告诉我们这个特征对目标变量的影响程度:β的绝对值越大,说明这个特征对目标变量的影响越大。
在房价预测的案例中,假设我们得到的模型参数表明,房屋的面积(单位:平方米)与房价的关系系数为2000。这意味着,如果其他条件不变,房屋的面积每增加一个平方米,其预测的房价就会增加2000元。同样,如果地理位置的参数系数为-50000,这说明房屋距离市中心的距离每增加一公里(假设地理位置特征是以距离市中心的公里数表示),预测的房价就会下降50000元。这些都是业务解读的例子,它们可以帮助我们理解房价是如何被各个特征所影响的。
# 获取模型参数
coef = model.coef_
intercept = model.intercept_
print('Coefficients:', coef)
print('Intercept:', intercept)
对模型参数的解读需要依赖于实际的业务知识和常识。例如,如果我们发现某个特征的系数极大,而这个特征在业务上的影响应该是微小的,那么我们就应该怀疑这个模型是否出现了过拟合。另一方面,如果一个重要的特征的系数接近于零,那么我们可能需要重新检查我们的数据,看看是否存在错误或遗漏。
总的来说,线性回归模型是一个非常实用的工具,它既可以帮助我们预测目标变量,也可以帮助我们理解特征和目标变量之间的关系。在实际应用中,我们需要结合业务知识和数据分析技巧,才能更好地利用线性回归模型。希望这个案例可以帮助你更好地理解线性回归,也希望你在未来的学习和工作中能够有效地应用线性回归。
超越线性回归
线性回归是一个强大而简单的工具,但并非所有问题都可以使用线性模型来解决。当我们的数据不满足线性假设,或者我们想要捕捉更复杂的模式时,我们需要考虑更复杂的模型。以下是一些常见的替代方案:
-
多项式回归:当我们的数据呈现出非线性关系时,多项式回归可以是一个很好的选择。多项式回归通过引入特征的高次项来捕捉非线性关系。例如,我们可以将线性回归模型 $y=\beta_0 + \beta_1x$ 扩展为二次多项式回归模型 $y=\beta_0 + \beta_1x + \beta_2x^2$。通过选择合适的多项式阶数,我们可以拟合出复杂的曲线。
-
决策树和随机森林:这些是非参数的机器学习模型,它们可以捕捉非线性和非单调的关系。决策树通过一系列的问题(如“房间数大于3吗?”)来预测目标变量。而随机森林是多个决策树的集合,它可以提高预测的准确性和稳定性。
-
支持向量机:支持向量机(SVM)最初是用于分类问题的,但通过引入核函数,它也可以用于回归问题。SVM回归可以捕捉复杂的非线性关系,且具有良好的泛化能力。
线性回归模型和其他模型的选择,往往取决于我们的任务和数据。例如,当我们的任务是分类问题时,我们通常会选择逻辑回归或支持向量机;当我们的数据具有复杂的非线性关系时,我们可能会选择多项式回归或决策树。而在某些情况下,我们可能会组合多个模型,形成一个强大的集成模型。
在下一篇文章中,我们将深入讨论逻辑回归模型,一个用于处理分类问题的强大工具。虽然逻辑回归和线性回归的名称相似,但它们用于解决的问题类型是完全不同的。线性回归用于处理连续的目标变量,而逻辑回归用于处理二元或多元的分类问题。然而,逻辑回归和线性回归的原理有很多相似之处,例如,它们都使用了梯度下降等优化方法,都可以通过正则化来防止过拟合。我们将在接下来的文章中详细讨论这些问题。
让我们来看一个具体的例子:假设我们正在研究房价和房屋面积的关系,但我们发现房价和房屋面积的关系并非线性,而是曲线关系。此时,我们可以使用多项式回归来建模:
from sklearn.preprocessing import PolynomialFeatures
# 创建多项式特征
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
# 使用线性回归来拟合多项式特征
model = LinearRegression()
model.fit(X_poly, y)
在这个例子中,我们首先创建了二次多项式特征,然后使用线性回归来拟合这些特征。通过这种方式,我们可以使用线性回归模型来捕捉非线性关系。
对于更复杂的非线性关系,我们可以使用决策树或随机森林。以下是一个使用随机森林的例子:
from sklearn.ensemble import RandomForestRegressor
# 创建随机森林模型
model = RandomForestRegressor(n_estimators=100)
# 训练模型
model.fit(X_train, y_train)
在这个例子中,我们创建了一个随机森林模型,并用训练数据来训练它。随机森林可以捕捉复杂的非线性关系,且不容易过拟合。
总的来说,当线性回归模型不足以描述数据的复杂性时,我们有多种选择可以考虑。选择哪种模型取决于我们的任务、数据和具体需求。我们应该了解每种模型的优缺点,以便在实际工作中做出正确的选择。在未来的文章中,我们将深入探讨更多的机器学习模型,敬请期待。
结语
线性回归是统计学和机器学习中的基础工具。由于其简洁性和可解释性,线性回归在实际应用中被广泛使用。从我们的房价预测实战案例中,你已经看到,如何利用线性回归模型,去处理实际问题,理解数据之间的关系。
然而,线性回归也有其局限性。最明显的是,线性回归假设特征和目标变量之间存在线性关系,这在许多真实世界的情况下可能不成立。此外,线性回归对异常值敏感,并且可能在面对非线性、高维度和大规模数据时遇到困难。
因此,我们需要超越线性回归,学习更复杂的模型,以应对更多样的问题。幸运的是,机器学习提供了大量的工具和方法供我们选择。在接下来的文章中,我们将深入探讨其中的一些模型,包括逻辑回归、决策树、支持向量机等。
逻辑回归,虽然名字中带有“回归”,但实际上是用于处理分类问题的。你会看到,尽管逻辑回归和线性回归的用途不同,但它们有许多共同的理论基础,例如梯度下降和正则化。在理解了线性回归后,你将更容易理解逻辑回归。
在后续的文章中,我们还会学习更多关于数据预处理、特征选择和模型评估的方法。这些技术是机器学习的重要组成部分,它们可以帮助我们更好地理解我们的数据,构建更强大的模型,并对模型的性能进行有效的评估。