1.简述

学习目标：  非标准小波分解（用S整数变换）

      小波分解过程：读取加入噪声后的图片后，数据即是高度*宽度个数据点。对此矩阵数据要做二维离散小波分解，二维小波变换和一维小波变换的区别从原理上来说就是一和二的关系。首先对数据做行分解，写入循环，有多少行就做多少次小波分解。对于每一行的数据来说，做小波分解就是一维的，而一维小波分解就是咱们要写的程序中的基石。选择小波，以Haar小波为例，也叫db1，用函数调用此小波，将咱们的数据（就是之前的行数据）先与高通做卷积得出高频系数，这里建议卷积过程别手写，计算太慢了，计算函数直接调用即可。然后使用下采样得出高频系数cD，再与低通做卷积加下采样得出低频系数cA。这里说明一下由于是下采样，所以得到的每个系数矩阵是原矩阵的一半大小。最后将低频系数cA和高频系数cD组成系数矩阵。这是一次小波分解，如果需要二次小波分解，则是按照小波分解定义，将第一次小波分解的低频系数cA作为第二次分解的输入重复卷积和采样操作，再得出新的cA、cD，编程写循环即可。回到咱们每一行都做一维小波分解，将做完行分解后得到的新矩阵再对每一列进行列分解，按照同样的道理将系数组合起来得到最终的矩阵（这里注意一下行分解的矩阵和列分解的矩阵在组合系数时的行列转换问题）。最终的矩阵分为四块，左上角是低频系数cA，其余三块分别是高频系数cH、cV、cD，具体形式是[cA，cH；cV，cD]。别忘了一维小波分解咱们能做好几次，二维也是，用同样的道理，低频系数cA进入下一层，还是先做行分解再做列分解然后出结果，也是写循环解决。到此小波分解结束。

整数小波S变换对图像进行分解和重构

题目：用整数小波的S变换对256*256 Lena灰度图像进行非标准方法的3级分解与重构。

 

本案例的意义在于通过实验体会到整数小波变换。案例并不是直接利用MATLAB工具箱中的已有小波函数对图象进行整数小波分解，而是用下面的分解公式进行小波分解和重构。

 

进行非标准小波分解，交替进行3次行变换和3次列变换。

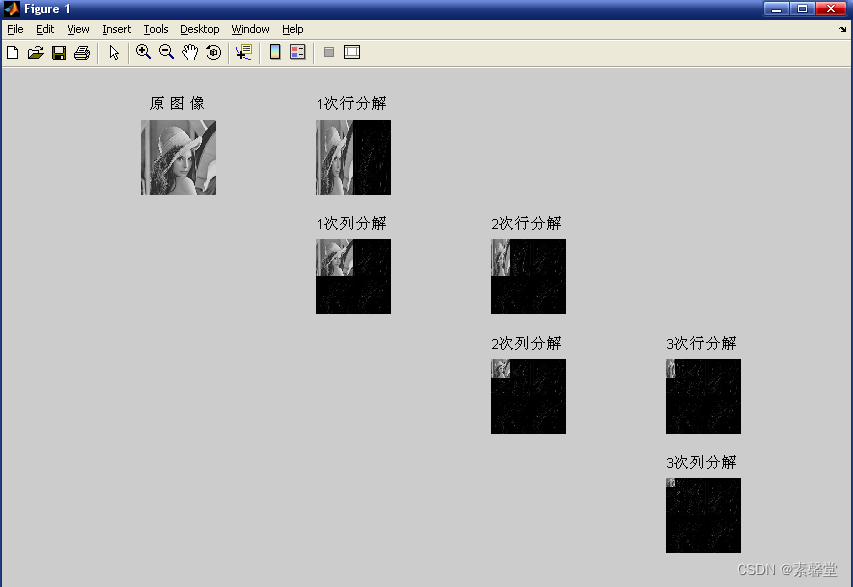
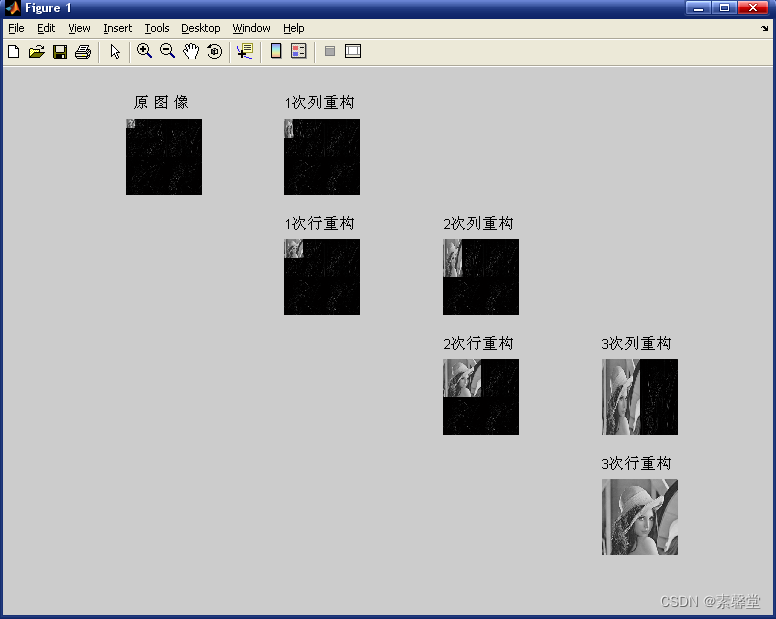
程序对每次变换后的结果都保存为位图文件，运行后可以在程序所在路径下看到保存的6个分解位图文件和6个重构位图文件。最后在一个图像中显示每次分解后的图像，便于对比。

 

实现方法：编写S变换的分解和重构子程序，分别对图像数据进行一次行列分解和列行重构，程序返回该次变换后的行列矩阵，在主程序中可以连续三次调用行列变换，即完成对原始图像的3级分解和重构，这里的变换是完全可逆的，也就是能够完全恢复原图像数据。通过对比3次重构后返回的数据与原图像数据后发现它们完全相同。

主要用的MATLAB工具函数有：

imread( )---------读取图像数据，为uint8类型，需变为double类型才能进行各种运算

imwrite()---------用于保存图像，这里用它来保存每一级变换后的图像

image( )----------显示图像，需要给出色谱表colormap，这里是灰度图，用colormap ＝gray（256）即可

subplot( )--------用于在一个窗口下绘制多个图像，在这里用于输出变换后的图像，以便对比。

更详细的内容请参考函数文件SDecompose.m和SRecompose.m，分别是分解和重构图像的函数，main.m是演示主程序。

注意事项：在首次成功后发现原图像数据和重构数据总有误差，但是根据S整数变换的可逆性，应该可以完全重构原始数据，在排除了是程序变换运算错误后，发现读出图像数据类型是uint8后，估计是该类型运算出错，上网搜索后终于找到症结所在：由于MATLAB读出的图像数据保存的是uint8类型（单字节0～255），它不能直接参与运算，在变为double类型后才可以进行运算。改造程序后，发现果然如此，此时原始数据和重构数据完全相同。

2.代码

主程序：
filename = input('Input the image file name: (size: 256×256 gray image)\nor press d key for default image:lena.bmp > ', 's');
if filename == 'd'
    filename = 'lena.bmp';
end
im = imread(filename);
de = SDecompose(im, 256);
input('Press any key to recompose the image ...'); 
re = SRecompose(de, 256);
 

子程序：

function imde = SDecompose( imMat, dim )
%%  非标准小波变换，用S整数变换3级分解图像数据，
% 输入参数imMat为原始256×256灰度图像数据方阵，
% imde为3级分解后的图像矩阵，分解灰度图
% S变换方法：分解式 Dj-1, k = Sj, 2k +1 - Sj, 2k；Sj-1, k =     Sj, 2k + [Dj-1, k / 2] 
% 重构式 Sj, 2k = Sj-1, k - [Dj-1, k / 2] Sj, 2k +1 = Dj-1, k + Sj, 2k
% 其中 S为对应图象数据
% dim = 256;
imMat = double(imMat);
map = gray(256);
subplot(4, 4, 1); image(imMat);colormap(map); title('原 图 像'); axis square; axis off;
% 对每一行和列交替进行第一次S分解变换
[imder, imdec] = decompose(imMat, dim);
% imder
% imdec
imgray = mat2gray(imder);          % 转为灰度矩阵
imwrite(imgray, 'imgraylr.bmp');   % 保存1次列变换后的灰度图
subplot(4, 4, 2); image(imder);colormap(map); title('1次行分解'); axis square; axis off;
imgray = mat2gray(imdec);
imwrite(imgray, 'imgray1c.bmp');
subplot(4, 4, 6); image(imdec);colormap(map); title('1次列分解'); axis square; axis off;

%%   对每一行和列交替进行第二次S分解变换
[imder, imdec] = decompose(imdec, dim/2);
imgray = mat2gray(imder);        % 转为灰度矩阵
imwrite(imgray, 'imgray2r.bmp'); % 保存2次行变换后的灰度图
subplot(4, 4, 7); image(imder);colormap(map); title('2次行分解'); axis square; axis off;
imgray = mat2gray(imdec);
imwrite(imgray, 'imgray2c.bmp');
%%     显示2次列变换后的灰度图
subplot(4, 4, 11); image(imdec);colormap(map); title('2次列分解'); axis square; axis off;

%%      对每一行和列交替进行第三次S分解变换
[imder, imdec] = decompose(imdec,dim/4);
imde = imdec;
imgray = mat2gray(imder);        % 转为灰度矩阵
imwrite(imgray, 'imgray3r.bmp'); % 保存3次行变换后的灰度图
subplot(4, 4, 12); image(imder);colormap(map); title('3次行分解'); axis square; axis off;

imgray = mat2gray(imdec);
imwrite(imgray, 'imgray3c.bmp');
subplot(4, 4, 16); image(imdec);colormap(map); title('3次列分解'); axis square; axis off;

%-----------------------------子程序decompose---------------------------------
function [imder, imdec] = decompose(imMat, dim)
%%   对每一行和列交替进行一次S分解变换, dim是维数
imder = imMat;
imdec = imMat;
for i = 1:dim                                                               % 对每一行进行S分解变换
    for j = 1:2:dim  
        imder(i, dim/2+(j+1)/2) = imMat(i, j+1) - imMat(i, j);              % 计算该行后半部分即Dj-1,k
        imder(i, (j+1)/2) = imMat(i, j) + floor(imder(i, dim/2+(j+1)/2)/2); % 计算该行前半部分即Sj-1,k
    end
end
%%  列变换
for i = 1:dim                                                             % 对每一列进行S分解变换
    for j = 1:2:dim
        imdec(dim/2+(j+1)/2, i) = imder(j+1, i) - imder(j, i); 
        imdec((j+1)/2, i) = imder(j, i) + floor(imdec(dim/2+(j+1)/2, i)/2);
    end
end

 

3.运行结果

 

3级分解效果图

                                                                      

 

 

3级重构效果图