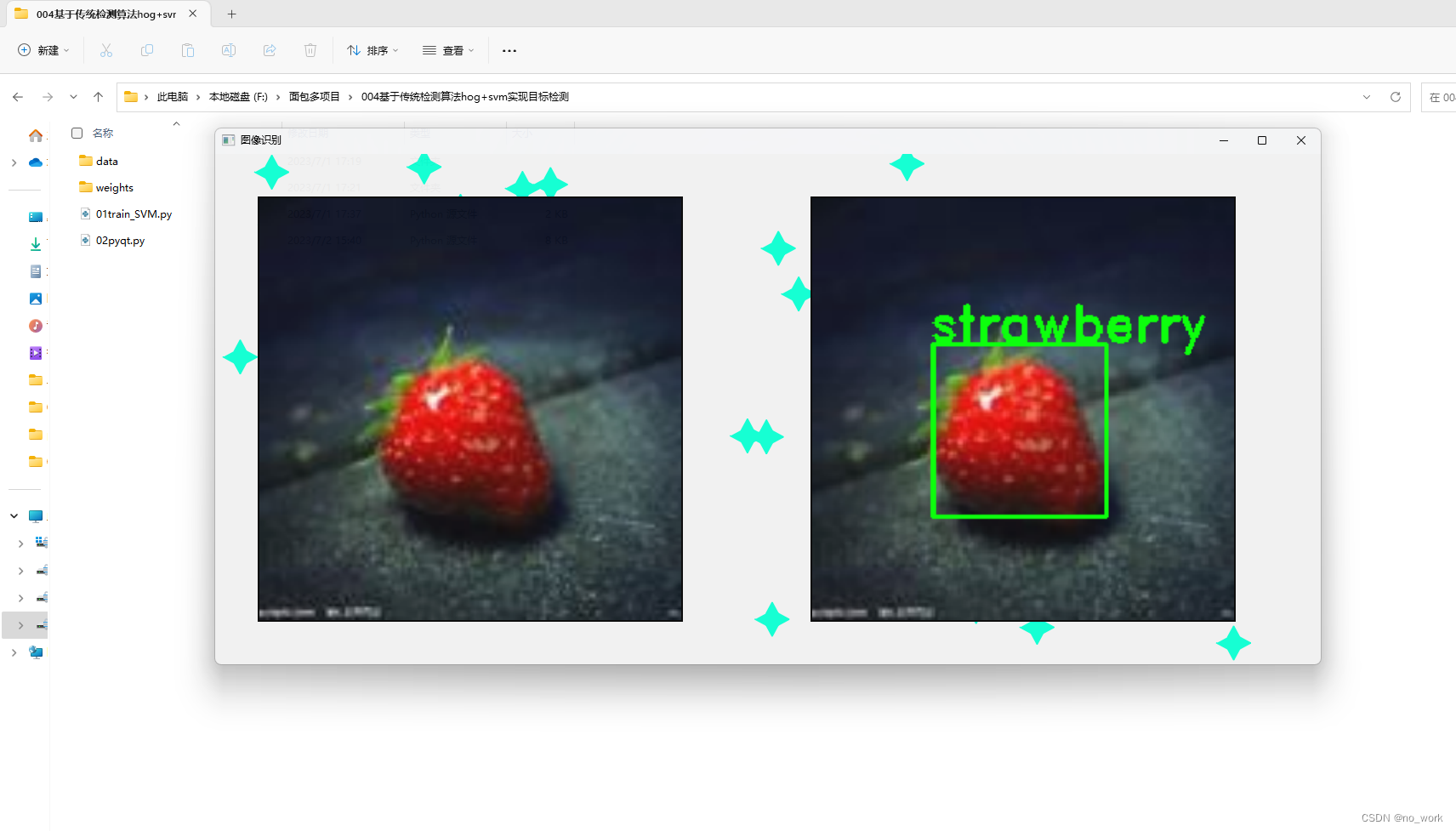
在这里提出一种算法，其实是将两篇papers的想法的结合。没有什么创新点，只是做一下算法原理的记录，防止后面重新看代码的时候一头雾水。

        算法的目的在于查找特定半径范围的圆，而不致力于查找所有的圆，当然它也支持查找所有的圆，只是精度没有在设定圆半径内搜索时精度来的高。

        算法具体的步骤是这样子的：

        1、二值化图像，并通过Canny算子找边缘，再只保留外边缘。

        2、行程行遍历整张图片，并用一个列表将圆弧像素点串起来，这里的原理类似于基于行程的连通域遍历，可以参考之前的文章基于行程标记的快速连通域提取。

        3、固定间隔提取串起来的圆弧上的5个点，并计算5个点的弧度变化绝对值的和，筛选剔除直线段。

        4、计算留存下来的圆弧段，提取首尾和中间三个点，大概计算其圆心。

        5、在圆形，从0到360度一圈，向外辐射遍历一定范围内的边缘点。

        6、基于高斯分布，提取所有距离固定半径较近的所有点，并计算这些点的离散分布中心，和所有点距离中心的平均距离，从而得出圆的中心和半径。

        接下来，仔细的介绍每一步。从第二步讲起:

行遍历整张图像

        我们采用如下的结构表示行中，相连的边缘像素:

struct arc_node
{
	int row;//相连边缘像素所在的行
	int start;//相连像素的起始列
	int end;//相连像素的终止列
	float arc;//当前边缘相对上一行边缘的弧度变化
	shared_ptr<arc_node> next;//指向下一行相连的边缘
	shared_ptr<arc_node> prev;//指向上一行相连的边缘
};

接着用如下结构来表示串接起来的所有边缘像素

struct arc_tree
{
	shared_ptr<arc_node> header;//串联的边缘像素点的头
	shared_ptr<arc_node> tail;//串联的边缘像素的尾

	int size;
};

在遍历的时候，注意两点：1、在同一行中，如果有两个边缘与上一行相接，则除了第一个之外，其余重新创建一个arc_tree(如图中的红色和蓝色边缘)。2、同一个tree里面的边缘点，如果arc变化绝对值超过一定的数值，则创建新的arc_tree(建议45度)。

 剔除直线边缘tree

        首先需要剔除tree的长度小于15的。接着，将tree从头到尾取5个点，并计算相邻3个点的arc的差值的绝对值之和，然后求均值，若在5度和45度之间，则表示可能为圆弧，否则予以剔除。

计算筛选过后的tree的圆心和半径

        取tree中的首尾和中间三个点，计算圆心，具体如下图所示:

图中橙色的点就是圆心，得到圆心之后，就可以计算半径。

计算最小似然圆

        从上一步计算得到的圆心，从0到360度，逐步遍历所有的边缘点，如下图所示。

 

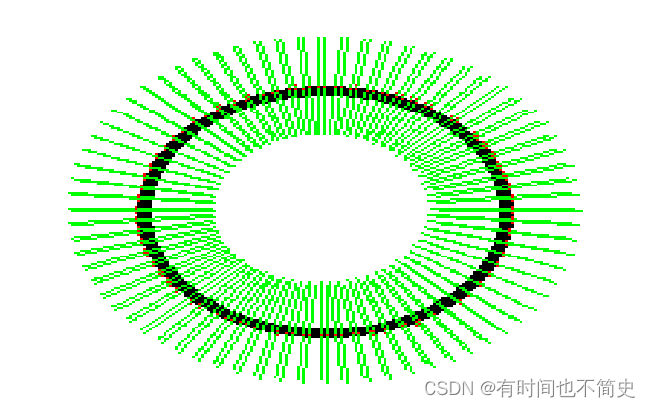
并通过如下所式计算每个像素点的比率：

如果比率值>0.6，则将这些点记录下来，最后如果点数如果在360度中，有270度的点在这个范围内，且所有比率值的均值超过一定值，表示为圆。这是就可以通过这些点计算其似然圆心和半径。