1 问题场景

对于ADAS算法开发，在工作中遇到过很多需要坐标系转换的场景。例如，一辆车上有很多个传感器，包括摄像头、毫米波雷达和激光雷达。在同一时刻感知到外部环境信息后，由于不同传感器基于自身坐标系，在数据融合之前需要将目标信息转换到同一个坐标系之下（通常是汽车后轴中心点）。

例如，下图中的XOY坐标系是以车辆后轴中心点为原点，车头方向为X轴正方向，垂直车身向左是Y轴正方向。X’O’Y’是前视摄像头坐标系，以摄像头位置为坐标原点，坐标轴方向和XY相同。

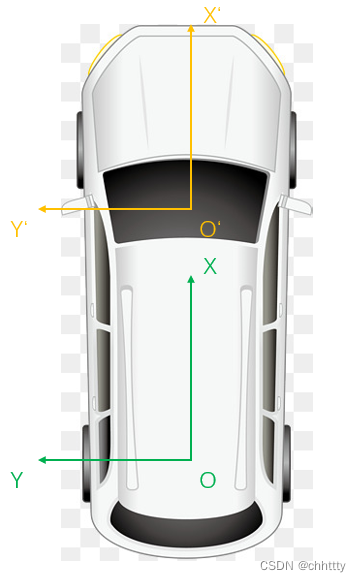
在这里插入图片描述
X’O’Y’坐标系相对于XOY坐标系向前平移一个距离，左右也相应的有一个距离。已知一个点P在X’O’Y’坐标系中的坐标为(x’,y’），以及已知O’点在XOY坐标系的坐标(xo’,yo’)，就可以通过坐标平移算出点P在XOY坐标系中的坐标。这是坐标系平移的例子。

再举个例子，车辆在运动的过程中，方向盘打了一个角度，汽车就会做一个圆周运动。在某一时刻t0，经过Δt时间，车辆不仅产生一个位置上的平移，自身还有一个旋转。

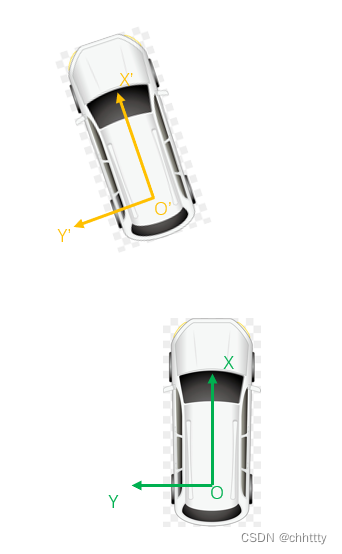
在这里插入图片描述
结合上图，比如说在t0时刻一个目标点在XOY坐标系下的坐标是(x,y)，在t1时刻车辆运动到前面一点的位置，并且车头朝向偏左了一个角度。这时候，那个目标点和车的相对位置就改变了，需要重新计算它在X’O’Y’坐标系中的坐标。利用X’O’Y’坐标系相对于XOY坐标系的距离和角度，就可以求出来目标点在心得坐标系X’O’Y’坐标系中的坐标(x’,y’)。这个例子中包含了坐标系的平移和旋转。

2 公式推导

上面场景的问题总结如下：已知点P在XOY坐标系中的坐标为(px,py)，X’O’Y’坐标系的原点O’在XOY坐标系中的坐标为(ox’,oy’)，求点P在X’O’Y’坐标系中的坐标。这里坐标系采用了右手系，即X向右Y向上。旋转角度定义为逆时针为正角度，以便后面的推导。

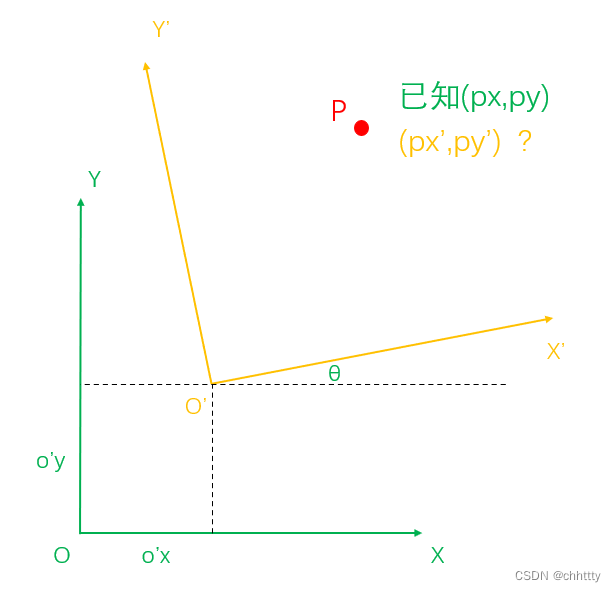
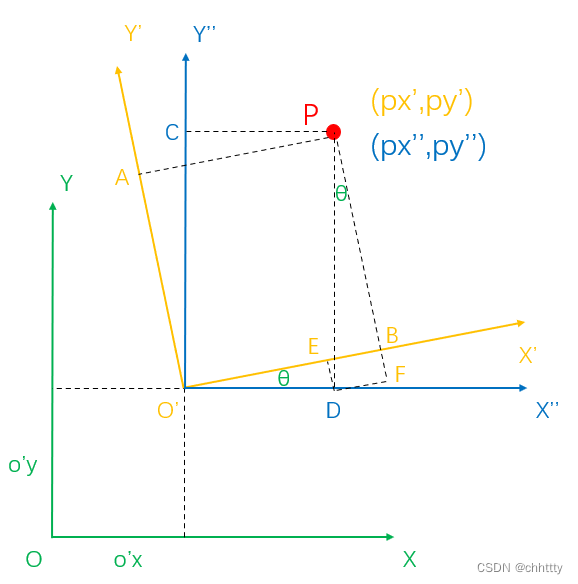
在这里插入图片描述

两个坐标系之间通过平移和旋转两种运动转换得到。为简化推导，首先基于O’点做出一个中间坐标系X’’O’Y’’，先完成旋转运动。

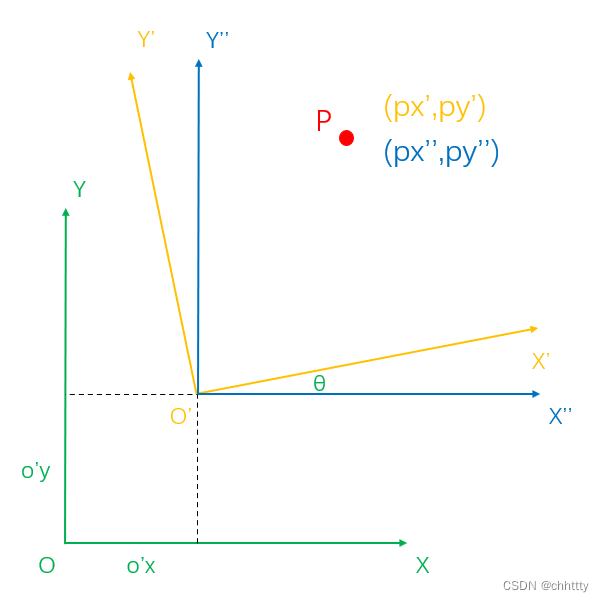
在这里插入图片描述

这里问题就转换为先推导(px’,py’)和(px’’,py’’)的关系，再推导(px’’,py’’)和(px,py)的关系。

2.1 旋转坐标系推导

首先，过点P做垂直线PA⊥O’Y’，PB⊥O’X’，PC⊥O’Y’’，PD⊥O’X’’，那么很容易知道∠BPD = θ，如下图所示。
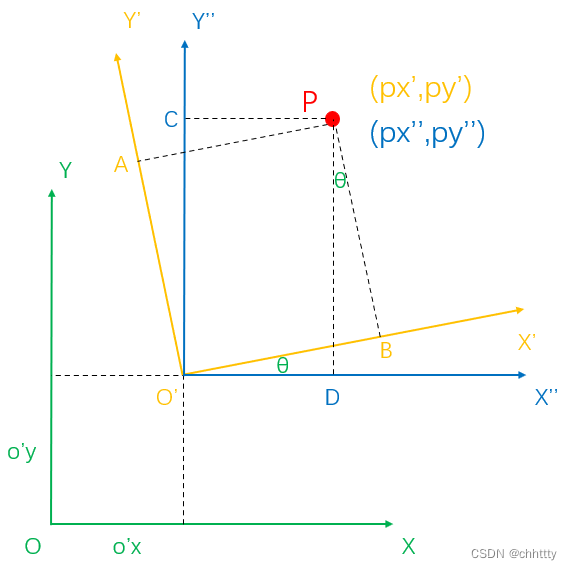
在这里插入图片描述
接着过点D做DE⊥O’X’，如下：

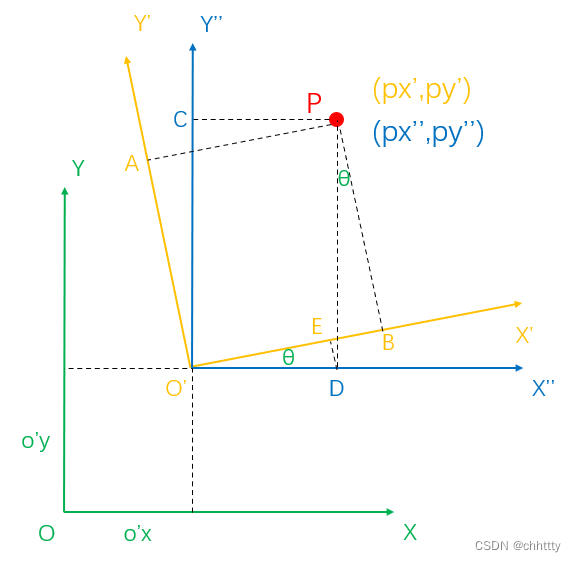
这样，就可以推导出px’：
$px'\;=\;\vert O'E\vert\;+\vert\;EB\vert\;=\;\vert O'D\vert\cdot\cos\theta\;+\;\vert PD\vert\cdot\sin\theta\;=\;px''\cdot\cos\theta\;\;+\;py''\cdot\sin\theta\;$

接着推导py’，过点D做DF⊥PF（PF是PB的延长线)，就可以推导出py’：
在这里插入图片描述
$py'\;=\;\vert PF\vert\;-\;\vert\;BF\vert\;=\;\vert PD\vert\cdot\cos\theta\;-\;\vert OD\vert\cdot\sin\theta\;=\;py''\cdot\cos\theta\;\;-\;px''\cdot\sin\theta\;$

将上面两个推导的结果写到一起，后面的章节需要用到：
$px'\;=\;px''\cdot\cos\theta\;\;+\;py''\cdot\sin\theta\;\\\; py'\;=-\;px''\cdot\sin\theta\;+\;py''\cdot\cos\theta\;\;$
这里也可以用矩阵变换的方式，一步就能得出这个结论。点P相当于绕着原点顺时针转了θ角度，所以通过旋转矩阵公式可以得出变换关系。
$\begin{bmatrix}px'\\py'\end{bmatrix}\;=\;\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\begin{bmatrix}px''\\py''\end{bmatrix}$

2.2 平移坐标系推导

平移的推导过程就简单很多，见下图
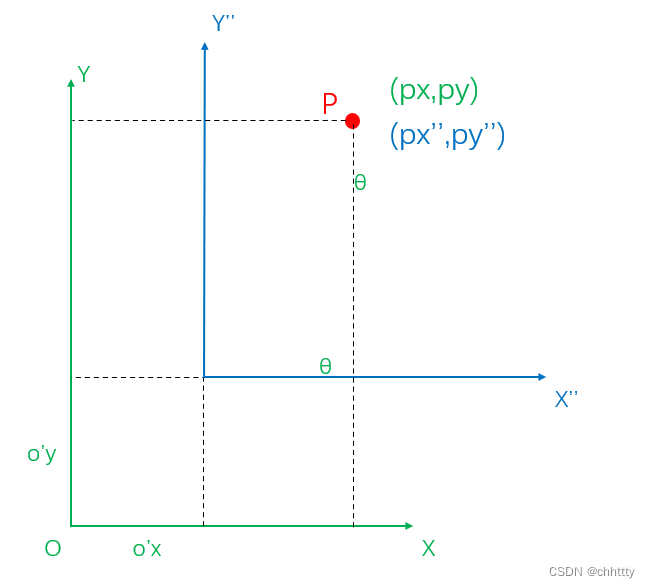
在这里插入图片描述
就是简单的加减：

$px''\;=\;px\;-\;o'x\\py''\;=\;py\;-\;o'y$

2.3 完整公式

将上面两个小节的公式代入得出完整公式：
$px'\;=\;(px\;-\;o'x)\cdot\cos\theta\;\;+\;(py\;-\;o'y)\cdot\sin\theta\;\\\; py'\;=-\;(px\;-\;o'x)\cdot\sin\theta\;+\;(py\;-\;o'y)\cdot\cos\theta\;\;$
后面基于这个公式编写C语言程序

3 C语言编程

首先，分析一下这个程序的需求。输入是一个点的在旧坐标系下的坐标，以及新坐标系相对于旧坐标系的位置和旋转角度。输出是该点在新坐标系下的坐标。

这里，博主设计一个简单的函数来实现这个算法。

#include <stdio.h>
#include <math.h>

#define PI 3.1415926F

typedef struct Point_Tag
{
    float X;
    float Y;
} Point_Type;//点结构体

typedef struct CoordinatePosition_Tag
{
    float deltaX;
    float deltaY;
    float theta;
} CoordinatePosition_Type;//新坐标系相对旧坐标系位置结构体

//坐标系变换函数
void coordinate_transformation(const Point_Type*              const point_old_system_sp,
                               const CoordinatePosition_Type* const coordinate_position_sp,
                                     Point_Type*              const point_new_system_sp)
{
    point_new_system_sp->X =  (point_old_system_sp->X - coordinate_position_sp->deltaX) * cosf(coordinate_position_sp->theta) +
                              (point_old_system_sp->Y - coordinate_position_sp->deltaY) * sinf(coordinate_position_sp->theta);
    point_new_system_sp->Y = -(point_old_system_sp->X - coordinate_position_sp->deltaX) * sinf(coordinate_position_sp->theta) +
                              (point_old_system_sp->Y - coordinate_position_sp->deltaY) * cosf(coordinate_position_sp->theta);
}

//main函数中简单测试
int main()
{
    Point_Type point_old_system;
    CoordinatePosition_Type coordinate_position;
    Point_Type point_new_system;

    point_old_system.X = 2.0F;
    point_old_system.Y = 2.0F;
    coordinate_position.deltaX = 0.0F;
    coordinate_position.deltaY = 0.0F;
    coordinate_position.theta = (45.0F/180.0F*PI);

    coordinate_transformation(&point_old_system,&coordinate_position,&point_new_system);

    printf("NEW_X = %f,NEW_Y = %f", point_new_system.X,point_new_system.Y);

}