线性动态规划的主要特点是状态转移的推导是按照问题规模 从小到大依次推导，较大规模的问题的解依赖较小规模的问题的解。

数字三角形：

[USACO1.5][IOI1994]数字三角形 Number Triangles - 洛谷https://www.luogu.com.cn/problem/P1216我们来看一道经典的问题数字三角形问题，这个问题应该是每一个学DP的人都会遇到的问题。

闫式DP分析法：

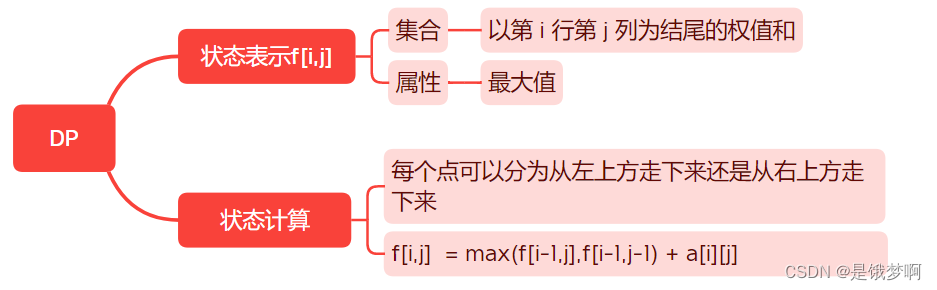
 算法分析：

我们用两维来表示状态，将f[i][j]分为从左上方走下来还是从右上方走下来,然后我们取一个max 最后加上该点的权值即可。

注意：

如果我们遇到f[i][j]的值存在负数的情况的时候，边界上的点（不存在从左上方的点和不存在右上方的点）在计算的时候可能出错，我们需要对f[i][j]进行初始化为负无穷即可。

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010,INF = 1e8;

int n,res;

int a[N][N],f[N][N];

int main()
{
	scanf("%d",&n);
	
	for(int i =1 ;i <= n ;i ++)
		for(int j = 1;j <= i ; j++)
			scanf("%d",&a[i][j]); 
	
	
	for(int i =1 ;i<= n ;i ++)
	{
		for(int j = 1 ;j <= i ; j++)
		{
			f[i][j] = max(f[i-1][j],f[i-1][j-1]) + a[i][j] ;
		}
	}
	
	
	for(int i =1 ;i<= n ;i ++)
	{
		res = max(res,f[n][i]);
	}
	
	printf("%d",res);
	
	return 0;
}

---

最长上升子序列：

最长上升子序列 - 洛谷https://www.luogu.com.cn/problem/B3637最长上升子序列也是一个经典的DP问题了，我们还是从闫式DP分析法开始分析。

闫式DP分析法：

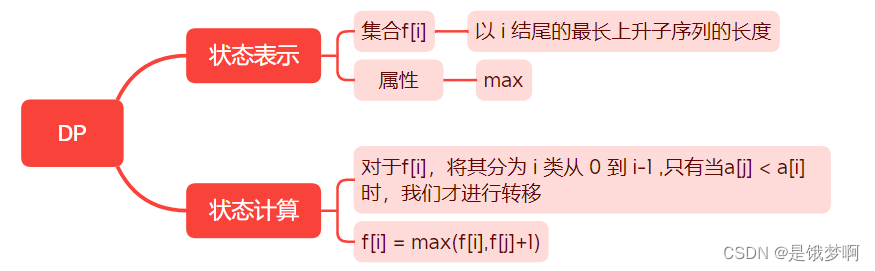
 算法分析：

对于 f[i]我们将其分为0 ~ i-1类，对于a[0] ~a[i-1](0 <= j <= i-1)，当存在a[j] < a[i] 时，说明以j结尾的序列可以接上 i ，进行状态转移。  

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1000010,INF = 1e8;

int n,res;
int a[N],f[N];

int main()
{
	scanf("%d",&n);
	for(int i = 1 ;i <= n ;i ++) cin >> a[i];
	
	for(int i = 1 ;i <= n ;i ++)
	{
		f[i] = 1; 
		for(int j = 1 ;j<= i-1 ;j ++)
		{
			if(a[j] < a[i])
			{
				f[i] = max(f[i],f[j] + 1);	
			} 
		}
		
		res = max(res,f[i]);
	}
	
	
	printf("%d",res);
	
	return 0;
} 

魔族密码： 

魔族密码 - 洛谷https://www.luogu.com.cn/problem/P1481

算法分析：

魔族密码是最长上升子序列的一个变种题目，换汤不换药，在最长上升子序列中我们的一个判断条件是是否在0 ~ i - 1中存在a[j] < a[i]，进行状态转移；我们这个题目和最长上升子序列的转移方程一模一样，只不过条件判断变成了0 ~ i - 1中的字符串是否是当前字符串的前缀。

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 2010,INF = 1e8;

int n,f[N],res;

string str[N];

int main()
{
	cin >> n;
	
	for(int i = 1 ; i <= n ;i ++) cin >> str[i];
	
	for(int i = 1 ;i <= n ;i ++)
	{
		f[i] = 1;
		for(int j = 1;j <= i - 1 ; j ++)
		{
			int len = str[j].length();
			if(str[i].substr(0,len) == str[j])
			{
				f[i] = max(f[i],f[j] + 1);
			} 
		}
		res = max(res,f[i]);
	}
	
	cout << res<<endl;
	
	return 0;
}

编辑距离： 

编辑距离 - 洛谷https://www.luogu.com.cn/problem/P2758

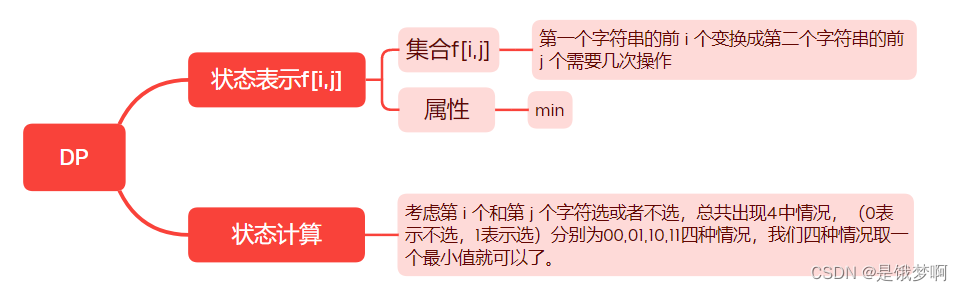
算法分析：

根据闫式DP分析法，我们考虑 i , j 选与不选；

当考虑前 i - 1 个字符和前 j 个字符，；

当考虑前 i 个字符和前 j - 1 个字符，；

当考虑前 i 个字符和前 j 个字符，我们需要曲线救国一下，考虑前i - 1 和前j - 1 个字符然后判断第i个字符和第j个字符是否相等，如果相等就不需要操作，如果不相等还需要一次操作。；

当考虑前 i -1 个字符和前 j - 1个字符的时候，我们发现其实这种情况已经包含在了前(i ,  j - 1) 和（i-1 , j）两种情况内了。

转移方程：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 2010;


char a[N],b[N];

int f[N][N],lena,lenb;

int main()
{
	scanf("%s%s",a + 1 , b + 1);
	
	lena = strlen(a + 1);
	lenb = strlen(b + 1);
	
	for(int i = 0; i <= lena;i ++)f[i][0] = i;
	for(int j = 0; j <= lenb;j ++)f[0][j] = j;
	
	for(int i =1; i<= lena; i++)
	{
		for(int j =1; j<= lenb ;j ++)
		{
			f[i][j] = min(f[i-1][j] + 1, f[i][j-1] + 1);
			f[i][j] = min(f[i][j],f[i-1][j-1] + (a[i]!=b[j]));
		}
	}
	
	printf("%d",f[lena][lenb]);
	
	return 0;
}