网络流
下面是本章需要掌握的知识
• 流量⽹络的相关概念
• 最⼤流的概念
• 最⼩割集合的概念
• Dinic有效算法的步骤
• 会⼿推⼀个流量⽹络的最⼤流
下面对此依次进行复习
首先看流量网络的相关概念
上面是课程PPT中的定义,真是抽象
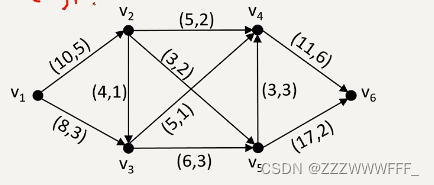
实际上,我们直接将某个流量网络进行建模出来就是上图这样,其中每一条弧上的第一个数字代表该条弧的最大流量,第二个数字代表该条弧的实际通过流量,并且定义一个发点V1、收点V6,其余的就是中间点了
那么上图所说的可行流又是什么?
实际上可行流即从发点到收点的流量都是合法的
- 即每一条弧的实际流量f>=0且f<=c
- 并且每个中间点的接收流量之和=发出流量之和
- 发点发出流量之和=收点接收流量之和
下面看前向弧、后向弧的概念
假设有一条链u,它链接了发点与收点,且定义链的方向是从发点到收点(注意链的方向与弧的方向无关)
那么链上的弧分为了
下面看增广链的概念
假设有一条从发点到收点的链,当该链满足如下条件时为增广链
- 如果链上的某条弧是前向弧,则必须满足0<=f<c,即是非饱和弧
- 如果链上的某条弧是后向弧,则必须满足0<f<=c,即是非零流弧
下面看割集的相关概念
割量也称为割集的容量
还是看一个例子
如上图所示,我们在流量网络上将发点和收点分开了
那么现在的割集为(v1,v2),(v1,v3)
现在的割量为5+6=11
这是一个割集与一个割量,但是我们将发点与收点分开的方式有多种,将它们都求出来,找到最小割量,就是找到最小割集了
定理:最小割量的大小就等于网络的最大流量
下面是Dinic的算法步骤
1. 从0流𝑓开始
2. 构造分层辅助网络
3. 如果𝐴𝑁 𝑓 存在s-t最短路径
① 求得𝐴𝑁 𝑓 上的极大流𝑔
② 叠加流𝑓 = 𝑓 + 𝑔;
GOTO 2
4. 否则, 𝑓为所求最大流
注意这里的分层网络是为了方便我们判断是否某条弧是否还有残余流量
并且在增广链的构建过程中则会判断是否找到的顶点的层数是当前顶点的层数+1(即还有残余流量)
算法设计与分析 课程期末复习简记(更新中)
news2026/2/11 23:19:18
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/710330.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Maynor的博客专家成长之路——暨2023年中复盘
文章目录 博客专家成长之路——暨2023年中复盘前言念念不忘的博客专家每天只做三件事敲代码写博客健健身 我的感悟 不足之处未来:和CSDN共同成长最后 博客专家成长之路——暨2023年中复盘
前言
2023年不知不觉已经过去了半年有余,也是时候作年中复盘…
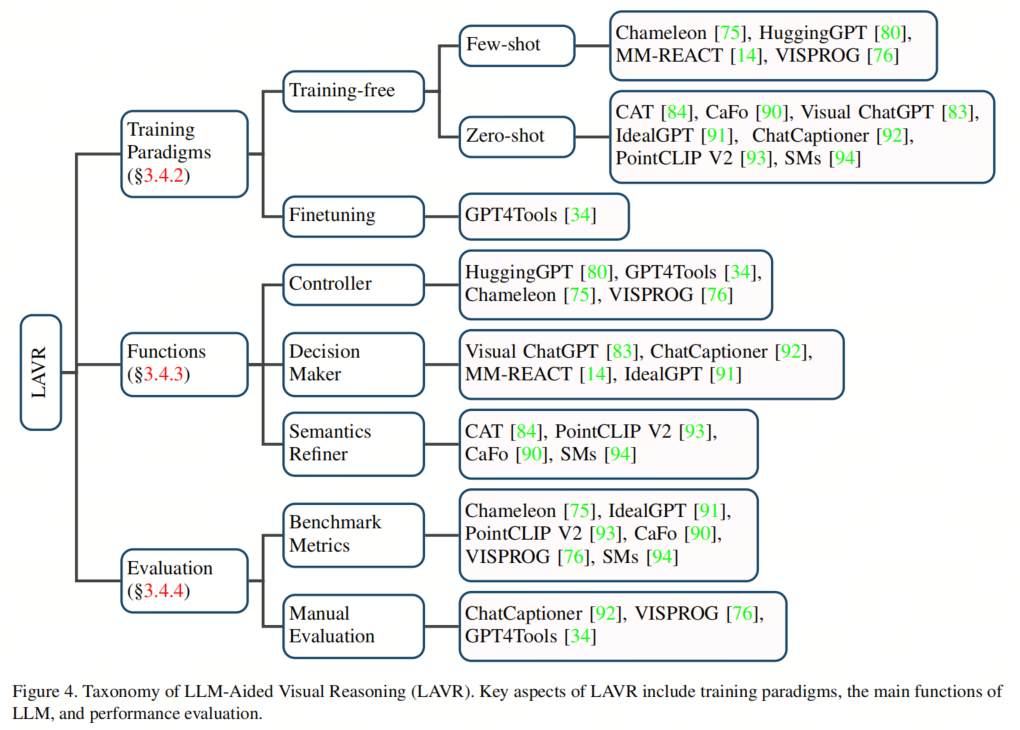
基于自然语言处理的多模态模型_综述
A Survey on Multimodal Large Language Models; 论文链接:https://arxiv.org/pdf/2306.13549.pdf 项目链接(实时更新最新论文,已获1.8K Stars):https://github.com/BradyFU/Awesome-Multimodal-Large-Language-Models 研究背景
…
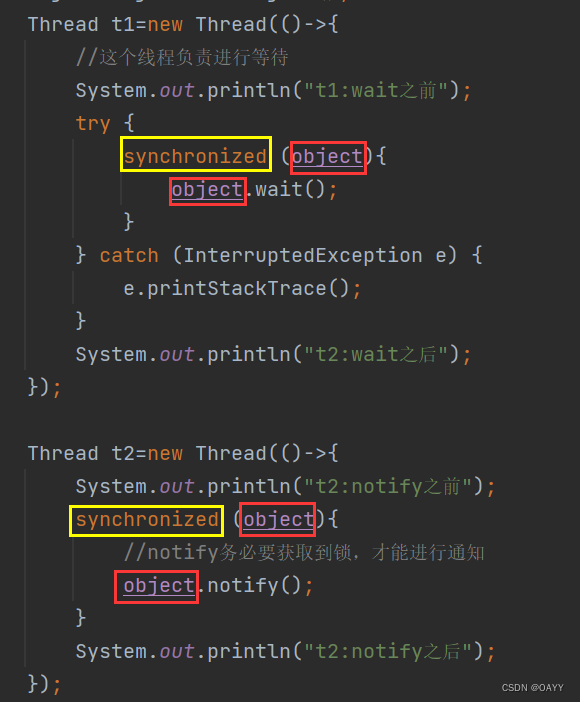
线程安全问题之原因及解决方案
线程安全问题 根本原因代码结构原子性解决方案:synchronized 内存可见性问题解决方案 volatile 指令重排序问题wait和notify判定一个代码是否线程安全,一定要具体问题具体分析!!! 根本原因 根本原因:多线程抢占式执行,随机调度。 …
ESP8266-NodeMCU搭建Arduino IDE开发环境
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、准备工作二、搭建步骤1.打开Arduino IDE 首选项2.打开Arduino IDE的“开发板管理器”3.在Arduino IDE的开发板菜单中找到“NodeMCU开发板”4.设置Arduino IDE的…
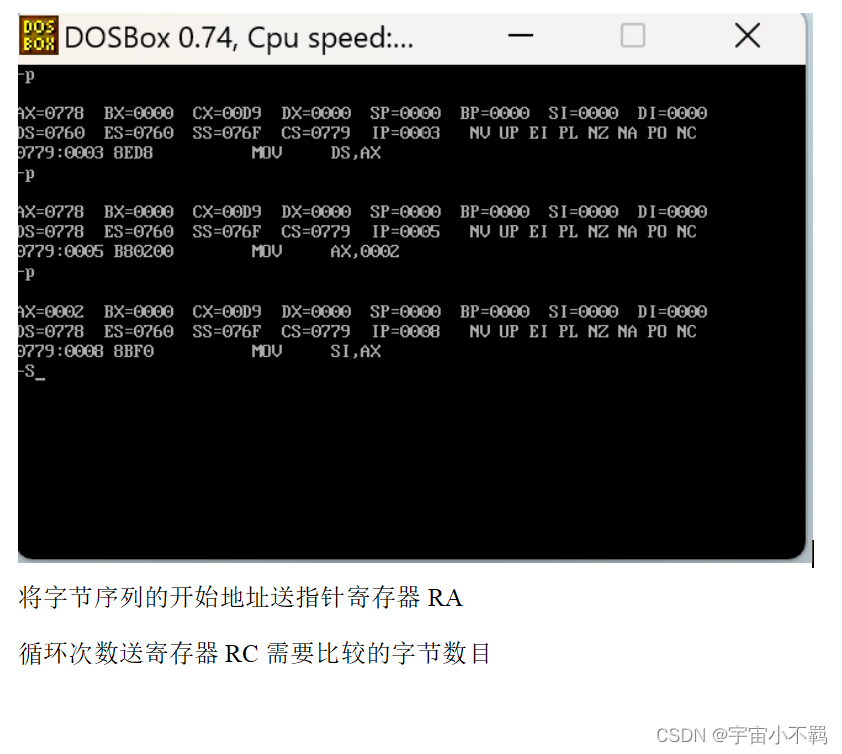
实验二:子程序设计实验
一、实验目的闻明找强的的掌握于程府的定又和调用方法掌握子程布的程库设计与调试方法 实验要求. 说明实现本实验需要掌握的知识及本实验害要的实验环境 二、实验要求了解萄单汇师培长程产没计与调武了解江编语子能店定义了解汇编语着子程序设计
实验内容 阐明实验具体内容及实…
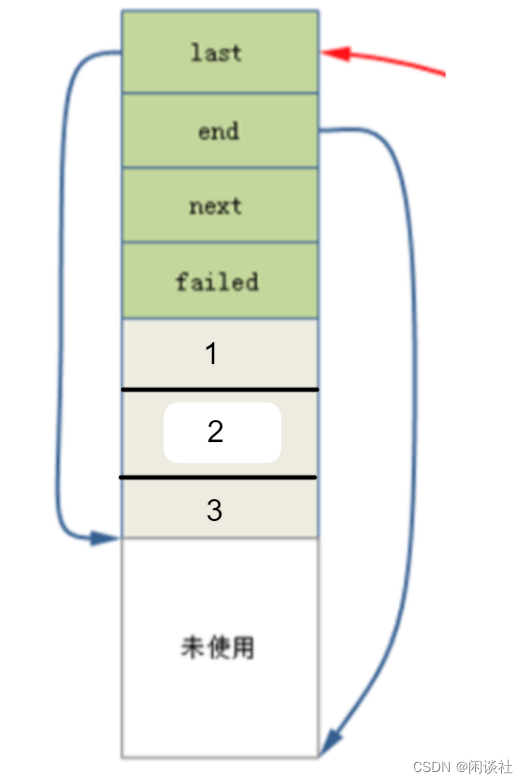
3. Linux组件之内存池的实现
文章目录 一、为什么需要内存池二、内存池的工作流程三、内存池的实现3.1 数据结构3.2 接口设计3.2.1 创建内存池3.2.2 内存池销毁3.2.3 内存分配1. 分配小块内存2. 分配大块内存 3.2.4 内存池的释放3.2.5 内存池重置 3.3 完整代码 一、为什么需要内存池
应用程序使用内存&…
【我们一起60天准备考研算法面试(大全)-第一天 1/60(排序、进制)】【每天40分钟,我们一起用60天准备 考研408-数据结构(笔试)】
专注 效率 记忆 预习 笔记 复习 做题 欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录) 文章字体风格: 红色文字表示&#…
与彭老师交流(北京大学 心理与认知科学学院)
交流:主要是了解人家在做什么对什么感兴趣,和让人家知道你在做什么对什么感兴趣,然后你觉得未来可以做什么有价值的事情。 1.老师做的方向里面有包含利用人工智能这一块的知识,我觉得我是可以做的,机理这一块的东西我不…
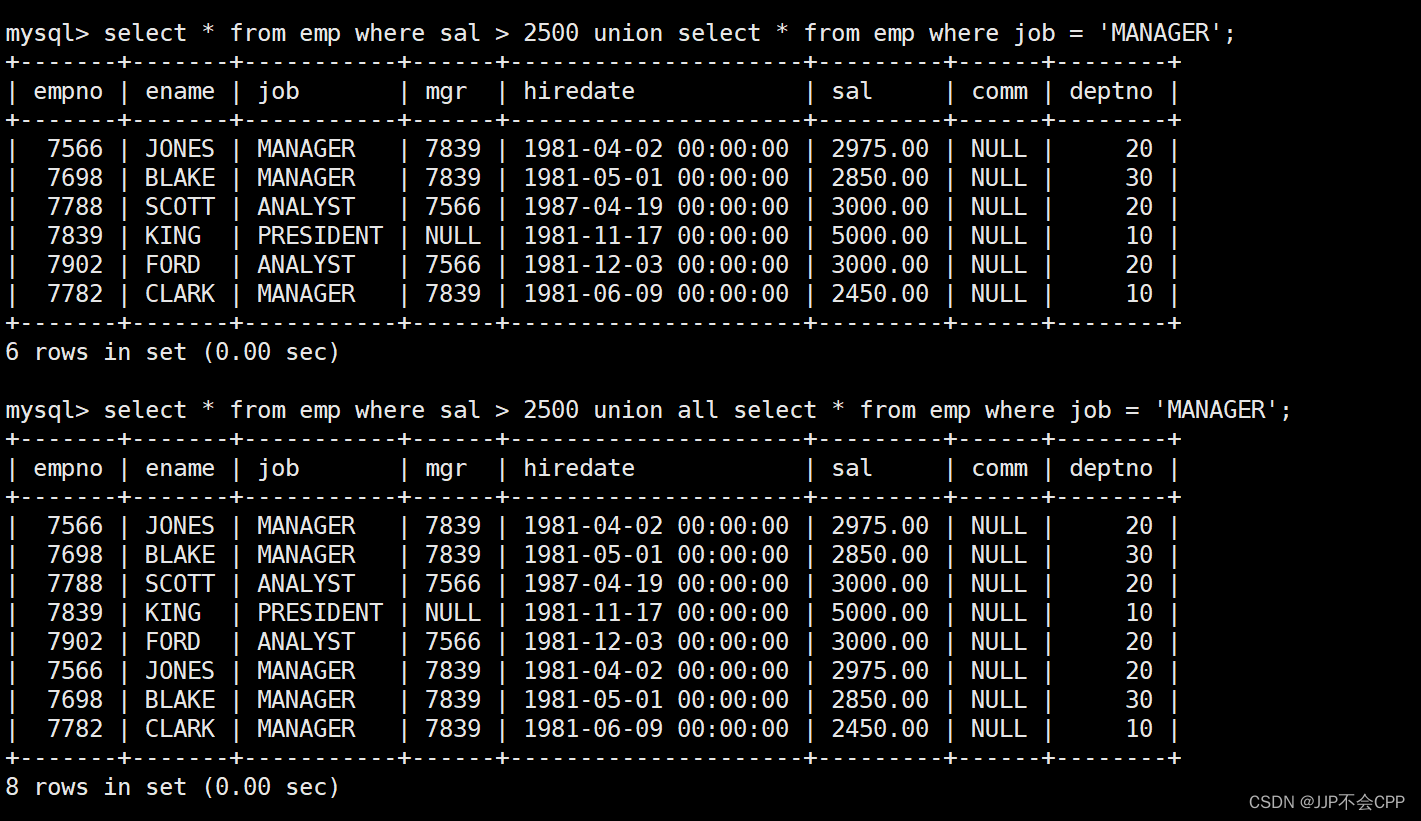
MySQL数据库复合查询
文章目录 一、多表查询二、自连接三、子查询1.单行子查询2.多行子查询3.多列子查询4.在from子句中使用子查询 四、合并查询 一、多表查询
在实际开发中,我们需要查询的数据往往会来自不同的表,所以需要进行多表查询。下面我们用一个简单的公司管理系统&…
启动游戏提示缺少(或丢失)xinput1_3.dll的解决办法
在我们打开游戏的或者软件的时候,电脑提示“找不到xinput1_3.dll,无法继续执行此代码”怎么办?相信困扰着不少小伙伴,我再在打开吃鸡的时候,然后花了一上午的时候时间研究,现在终于知道xinput1_3.dll文件是…
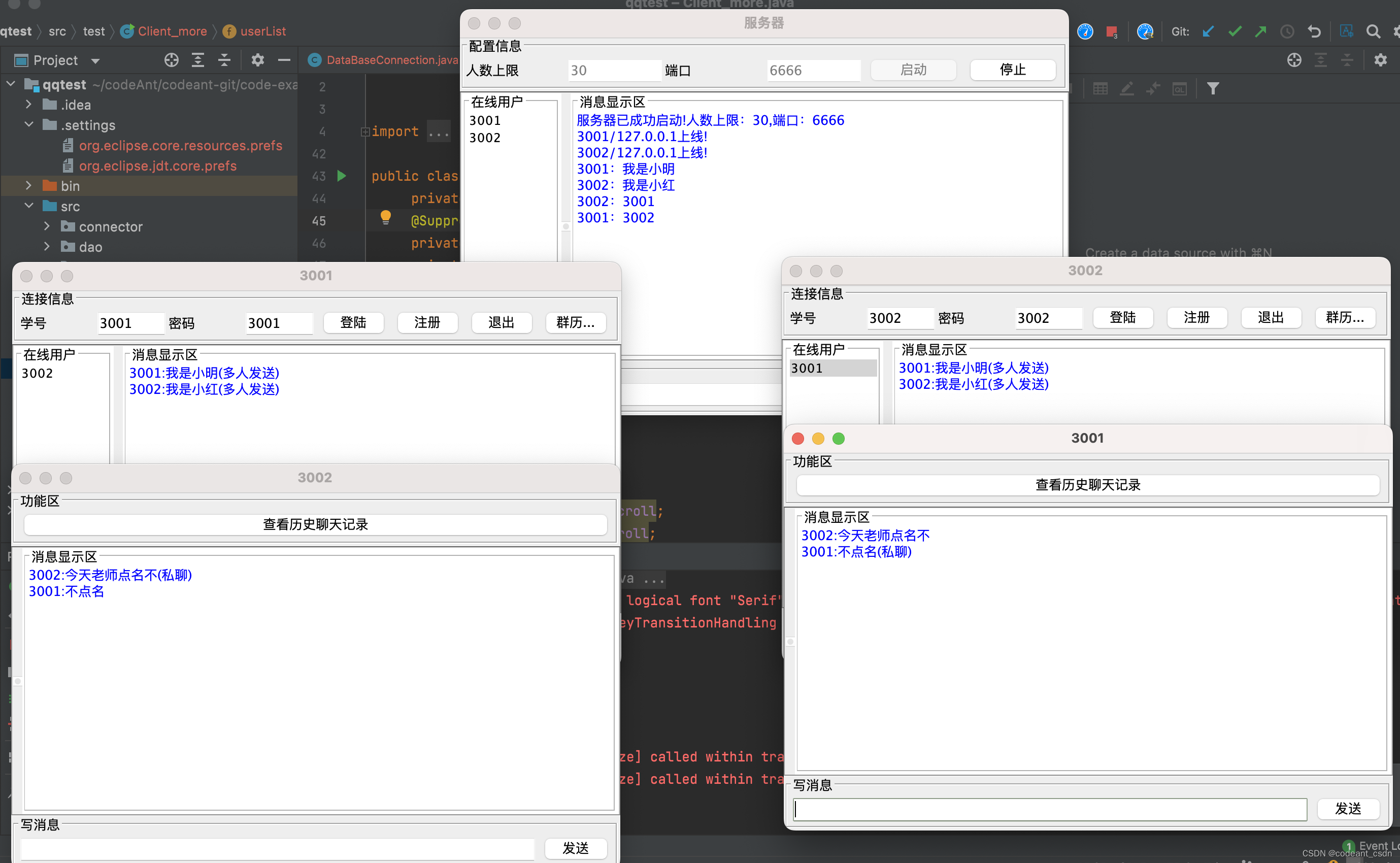
基于TCP协议实现多人在线的聊天室
基于TCP协议实现多人在线的聊天室
程序采用CS架构,功能支持注册,登录,退出,私聊,群聊,查看历史信息。属于Java Swing窗口程序。
技术:Java swing,mysql
开发工具:IDEA…
性能测试之全链路压测流量模型你了解多少
目录 前言
基于业务模型实现
基于流量录制回放
灰度分流
总结: 前言
现在全链路越来越火,各大厂商也纷纷推出了自己的全链路压测测试方案。特别是针对全链路压测流量模型,各家方案都有所不同。最近我看了一些这方面的资料,有…
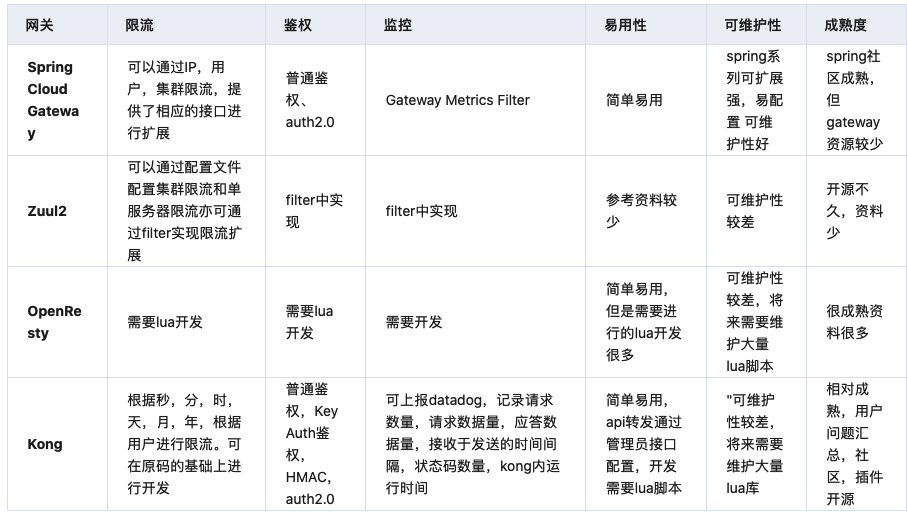
万能的网关系统设计方案,一篇带走
本文准备围绕七个点来讲网关,分别是网关的基本概念、网关设计思路、网关设计重点、流量网关、业务网关、常见网关对比,对基础概念熟悉的朋友可以根据目录查看自己感兴趣的部分。 什么是网关
网关,很多地方将网关比如成门, 没什么…
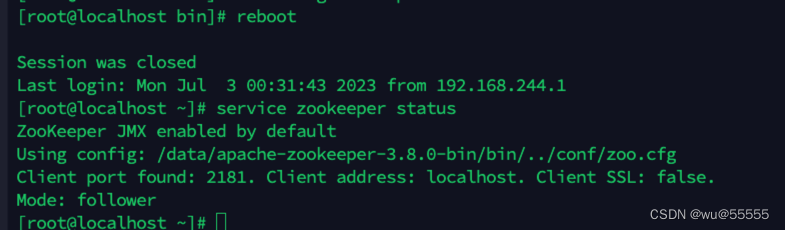
mac pro m1:搭建zookeeper集群并设置开机自启
0. 引言
之前我们讲解过搭建zookeeper单节点,但在实际生产中,为了保证服务高可用,通常我们是采用集群模式。所以本次我们来实操集群模式的搭建
1. zk集群模式
zk可以作为注册中心和配置中心,常用在微服务各类组件的多节点服务治…
Tomcat优化及部署
目录
一、Tomcat概述
二、Tomcat核心组件
1.Web容器
2.servlet容器
3.JSP容器
三、Tomcat的功能组件
1.connector
2.container
3.service
四、Tomcat部署
1.关闭防火墙和安全机制
2.将安装 Tomcat 所需软件包传到/opt目录下
3.安装JDK 4.设置JDK环境变量
5.编写j…
链路性能测试中参数多样性方法分享
目录
业务无关量
随机数字
线程安全随机
随机字符串
业务相关量
随机相关量
上游接口获取
上游接口造数据
提前造数据
总结: 下面分享几种我工作中常用到的增加参数多样性的方法。
业务无关量
这个是最常用到的,当部分的接口参数对接下来的用…
机器人开发--EKF扩展卡尔曼滤波介绍
机器人开发--EKF卡尔曼滤波介绍 1 介绍1.1 概述KF (Kalman Filter)EKF (Extended Kalman Filter)UKF (Unscented Kalman Filter) 1.2 发展历史1.3 卡尔曼演化分支1.4 应用1.5 特点1.6 姿态估计问题 from 南叔先生1.7 EKF、PF、UKF 对比1.8 EKF 递归框架 2 理解機器人學…
使用Matplotlib画三维图
使用matplotlib画3D图:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 创建X和Y的网格点
x np.linspace(-5, 5, 100)
y np.linspace(-5, 5, 100)
X, Y np.meshgrid(x, y)# 创建Z的网格点(这里使用一…
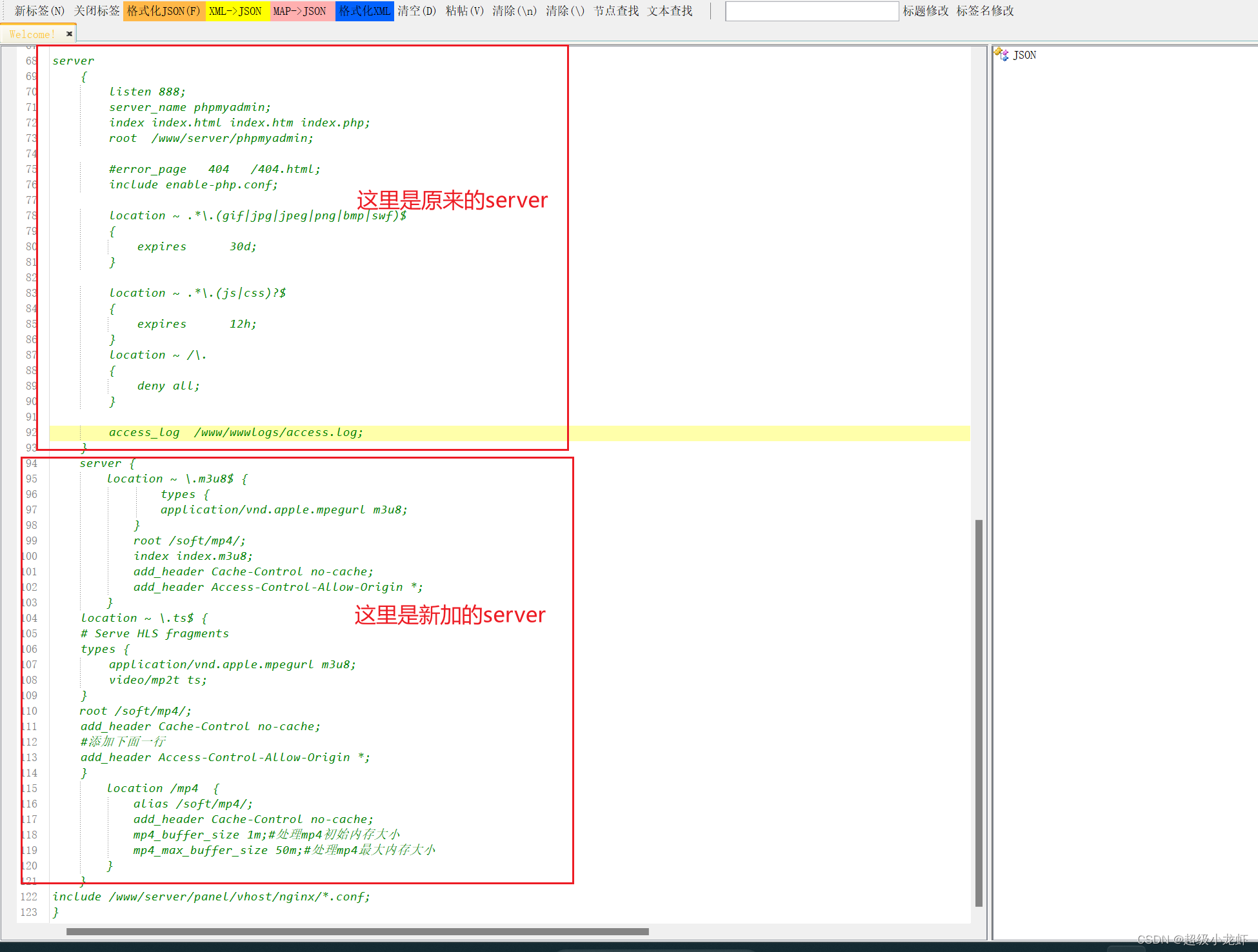
nginx 配置m3u8播放视频
第一步nginx配置:
参考 csdn - CircleMouse
Nginx配置搭建m3u8格式的视频播放服务 user www www;
worker_processes auto;
error_log /www/wwwlogs/nginx_error.log crit;
pid /www/server/nginx/logs/nginx.pid;
worker_rlimit_nofile 51200;stream {l…