状态估计乃传感器之本质。（To understand the need for state estimation is to understand the nature of sensors.）

任何传感器，激光也好，视觉也好，整个SLAM系统也好，要解决的问题只有一个：如何通过数据来估计自身状态。每种传感器的测量模型不一样，它们的精度也不一样。换句话说，状态估计问题，也就是“如何最好地使用传感器数据”。–高翔

1 介绍

1.1 概述

KF (Kalman Filter)

• 对于统计和控制理论，卡尔曼滤波，也称为线性二次估计( LQE ) ，是一种算法，它使用随时间观察的一系列测量值，包括统计噪声和其他不准确性，并生成往往更准确的未知变量的估计值。通过估计每个时间范围内变量的联合概率分布，比仅基于单个测量的结果更准确。该滤波器以鲁道夫·卡尔曼 (Rudolf E. Kálmán)【美国：匈牙利移民】的名字命名，他是该滤波器理论的主要开发者之一。
• 卡尔曼滤波,也称为线性二次估计(LQE).它使用时域上一系列包含统计噪声和其他误差的观测量,对未知变量进行估计。这种方法因为对每个时间段上未知变量的联合概率分布做了估计，因此比基于单一观测值预测更加精确。
• 这种数字滤波器有时被称为斯特拉托诺维奇-卡尔曼-布西滤波器，因为它是苏联数学家 鲁斯兰·斯特拉托诺维奇 (Stratonovich) 早期开发的更通用的非线性滤波器的特例。事实上，一些特殊情况的线性滤波器方程出现在斯特拉托诺维奇 1961 年夏天之前发表的论文中，当时卡尔曼在莫斯科的一次会议上与斯特拉托诺维奇会面。
• 该算法的工作过程分为两阶段。在预测阶段，卡尔曼滤波器生成当前状态变量及其不确定性的估计。一旦观察到下一个测量的结果（必然会受到一些误差，包括随机噪声的影响），这些估计值就会使用加权平均值进行更新，并且对具有更大确定性的估计值给予更多的权重。该算法是递归的。它可以实时运行，仅使用当前的输入测量值和先前计算的状态及其不确定性矩阵；不需要额外的过去信息。

EKF (Extended Kalman Filter)

• 经典的卡尔曼滤波只适用于线性系统，但我们知道真实世界中大多数情况下的系统都是非线性的。Bucy和Sunahara等人提出并研究了扩展卡尔曼滤波(Extended Kalman Filter，EKF)，将卡尔曼滤波理论进一步应用到非线性领域。
• 在估计理论中，扩展卡尔曼滤波器( EKF ) 是卡尔曼滤波器的非线性版本，它对当前均值和协方差的估计进行线性化。在明确定义的转换模型的情况下，EKF 已被认为是非线性状态估计、导航系统和GPS理论中的事实标准。
• 大部分工作是在美国宇航局艾姆斯研究中心完成的。EKF 采用微积分技术，即多元泰勒级数扩展，使模型关于工作点线性化。

UKF (Unscented Kalman Filter)

无迹卡尔曼滤波器。通过扫点方式，解决斜率，失真的问题。
UKF 需要对矩阵做2次分解，矩阵一旦不正定将导致算法奔溃，难以分析原因。这导致UKF在学术界用的较多，工业界较少，汽车行业基本不用。-- from 贝叶斯滤波与卡尔曼滤波第十四讲 无迹卡尔曼滤波

1.2 发展历史

年份	事件	相关论文/Reference
1960	卡尔曼提出离散系统的卡尔曼滤波理论	R. E. Kalman. (1960). A new approach to linear filtering and prediction problems. Journal of Basic Engineering Transactions, 82, 35-45.
1961	卡尔曼与Richard S. Bucy合作提出了连续系统的卡尔曼滤波理论	Kalman, R. E., & Bucy, R. S. (1961). New Results in Linear Filtering and Prediction Theory. Trans. ASME, Ser. D, J. Basic Eng (Vol.83, pp.109).
1960s	Stanley F. Schmidt首次实现了卡尔曼滤波器，并将其用在了阿波罗飞船的导航系统中
1960s	Bucy和Sunahara等人提出并研究了扩展卡尔曼滤波(Extended Kalman Filter，EKF)，将卡尔曼滤波理论进一步应用到非线性领域
1989	Singhal和Wu首次提出了全局卡尔曼滤波作为神经网络的学习算法	Singhal, S., & Wu, L. (1989). Training Multilayer Perceptrons with the Extended Kalman Algorithm. neural information processing systems.
2003	Shahjahan等人结合卡尔曼滤波和剪枝算法对神经网络的结构进行优化，减少了复杂度和存储空间，改善了过拟合的问题	Shahjahan, M., Akhand, M. A., & Murase, K. (2003). A pruning algorithm for training neural network ensembles. Nano Today, 628-633.

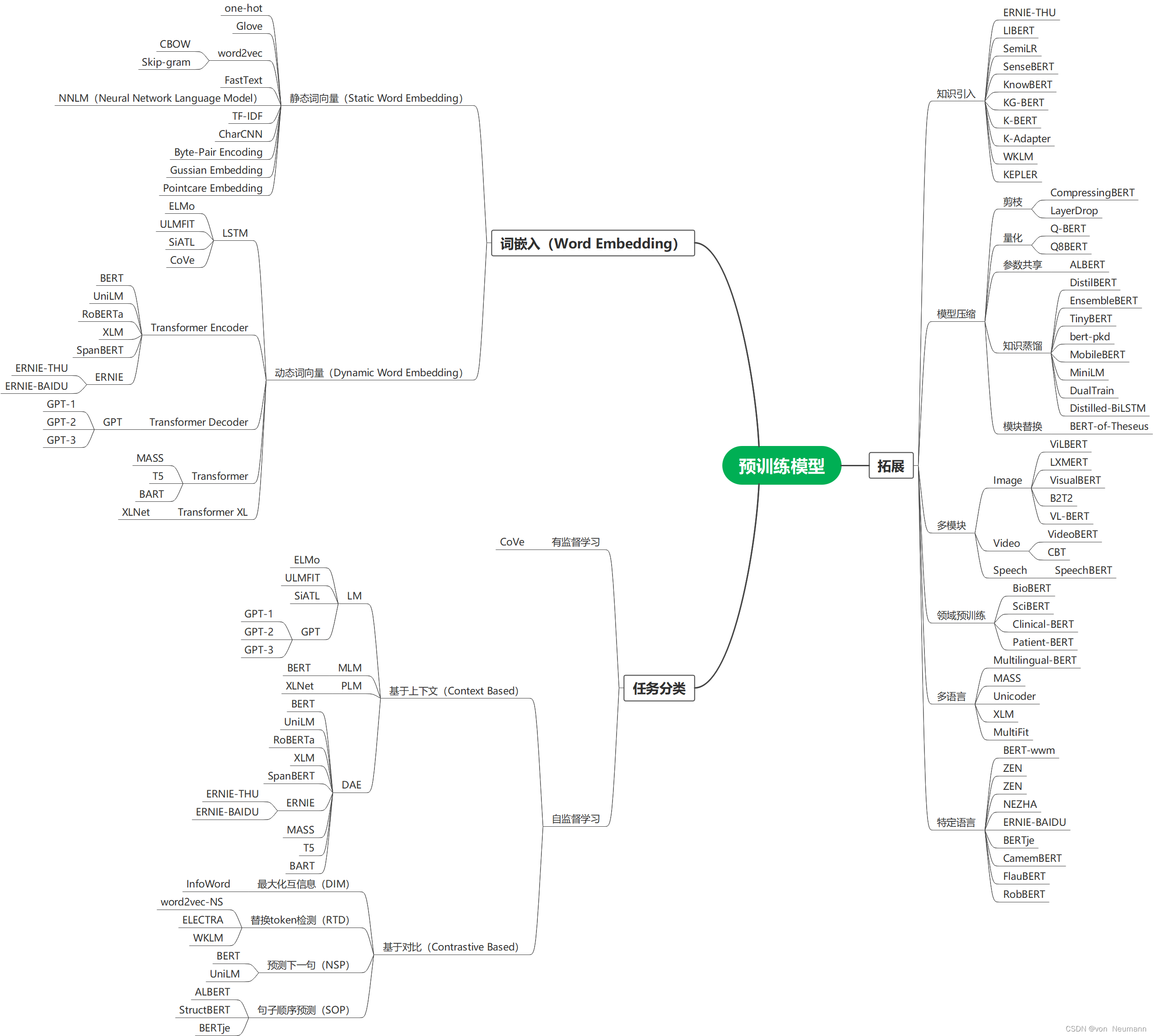
1.3 卡尔曼演化分支

• KF：（简单）卡尔曼滤波器
• Kalman–Bucy filter：卡尔曼-布西滤波器
• EKF：施密特 (Schmidt) 的扩展卡尔曼滤波器

1.4 应用

• 车辆的制导、导航和控制，特别是动态定位的飞机、航天器和船舶。
• 卡尔曼滤波是一个广泛应用于信号处理和计量经济学等主题的时间序列分析中的概念。
• 卡尔曼滤波也是机器人运动规划和控制的主要主题之一，可用于轨迹优化。
• 卡尔曼滤波也适用于建模中枢神经系统对运动的控制。由于发出电机命令和接收感官反馈之间存在时间延迟，卡尔曼滤波器的使用提供了一个现实的模型，用于估计电机系统的当前状态并发出更新的命令。
• 导弹、航天领域：卡尔曼滤波器在美国海军核弹道导弹潜艇导航系统的实施以及美国海军战斧导弹和美国空军空射巡航导弹等巡航导弹的制导和导航系统中发挥着至关重要的作用。它们还用于可重复使用运载火箭的制导和导航系统以及停靠在国际空间站的航天器的姿态控制和导航系统。
• 调频(FM) 收音机、电视机、卫星通信接收器、外层空间通信系统等都有应用。
• 图像处理领域的人脸识别、图像分割、图像边缘检测等都用到了卡尔曼滤波。
• 电池 BMS中，用 EKF 修正SOC。

1.5 特点

• 轻量化，硬件资源消耗很小
  The Apollo computer used 2k of magnetic core RAM and 36k wire rope […]. The CPU was built from ICs […]. Clock speed was under 100 kHz […]. The fact that the MIT engineers were able to pack such good software (one of the very first applications of the Kalman filter) into such a tiny computer is truly remarkable.
  — Interview with Jack Crenshaw, by Matthew Reed, TRS-80.org (2009)

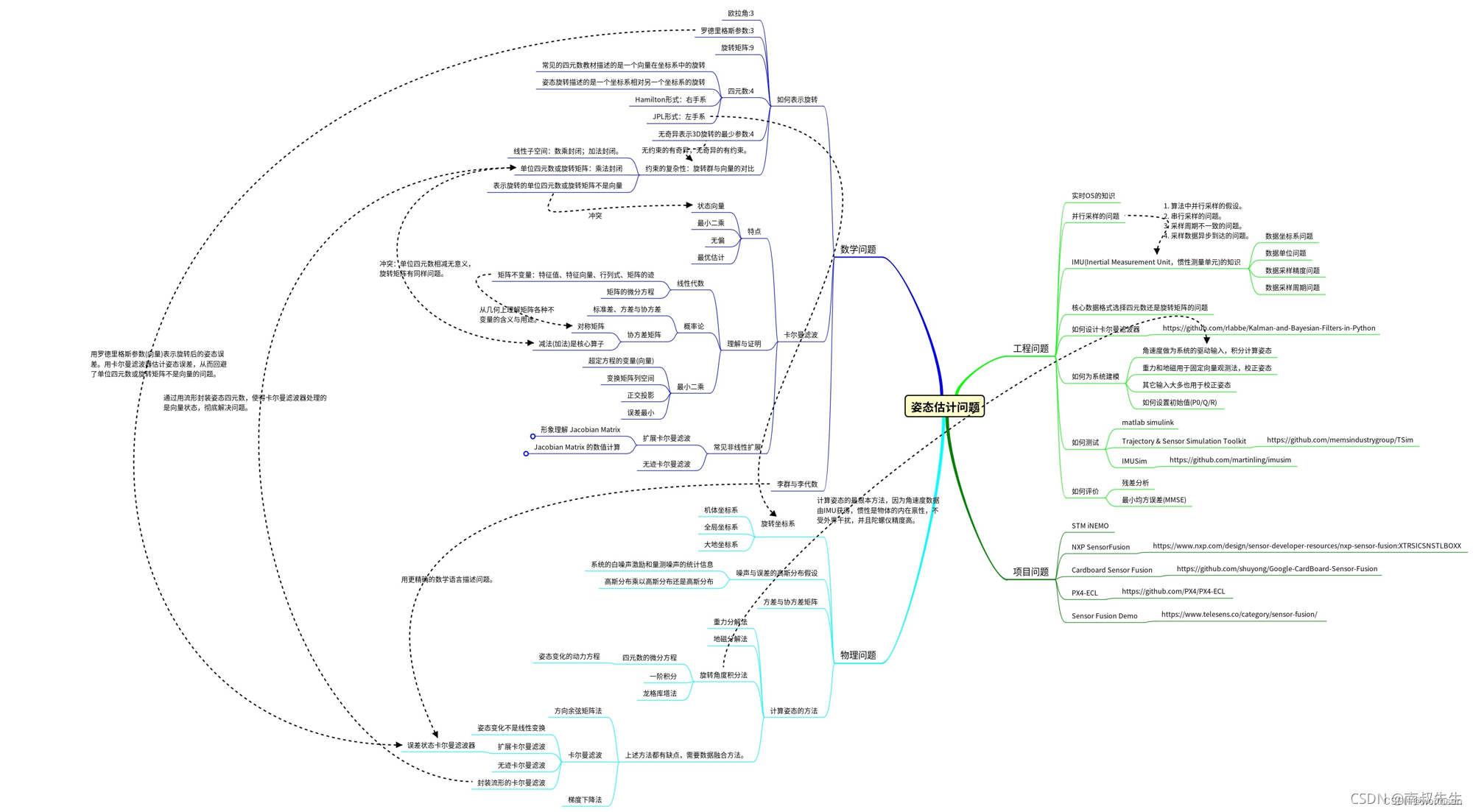
1.6 姿态估计问题 from 南叔先生

Kalman滤波通俗理解+实际应用

1.7 EKF、PF、UKF 对比

from 贝叶斯滤波与卡尔曼滤波第十四讲 无迹卡尔曼滤波

算法	速度	精度	稳定
EKF	快	差	较稳定
PF	慢	高	较稳定
UKF	较快	较高	很不稳定，易崩溃 维度越高越容易崩溃

UKF：学术界用的较多，工业界较少，汽车行业基本不用。

1.8 EKF 递归框架

from Tutorial: The Kalman Filter

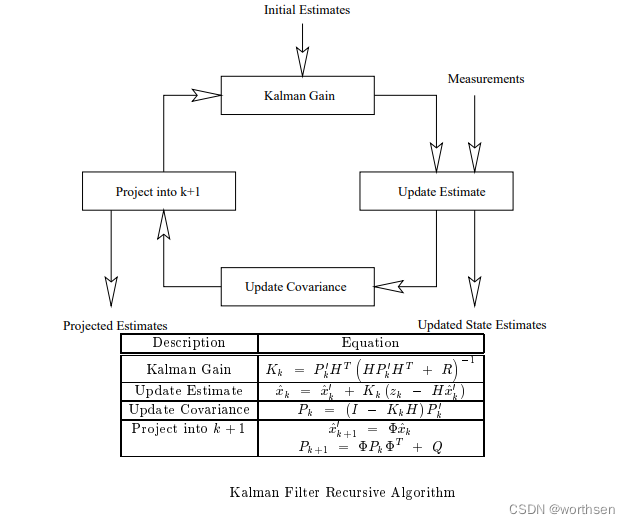
2 理解

機器人學：多軸旋翼機 Lec11 - 卡爾曼濾波器、擴展卡爾曼濾波器、無損卡爾曼濾波 KF、EKF、UKF

機器人學：多軸旋翼機 Lec11 - 卡爾曼濾波器、擴展卡爾曼濾波器、無損卡爾曼濾波 KF、EKF、UKF

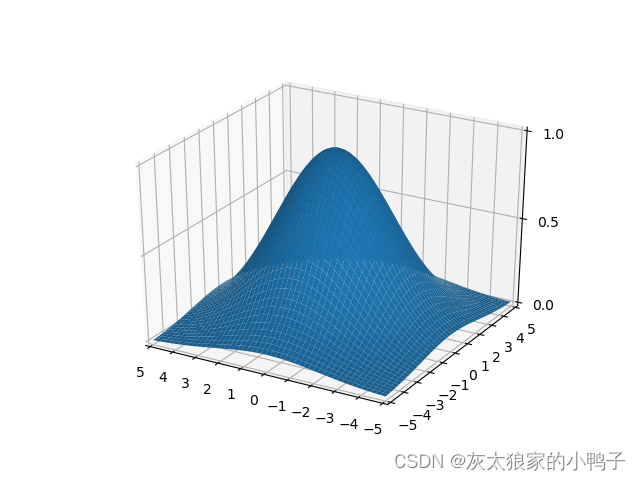
正态分布（Normal Distribution），又名高斯分布（Gaussian Distribution）。若随机变量 X 服从一个数学期望为 μ、方差为 ${\sigma }^2$ 的正态分布，记为 $N(\mu ，{\sigma }^2)$ 。其概率密度函数为正态分布的期望值 μ 决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

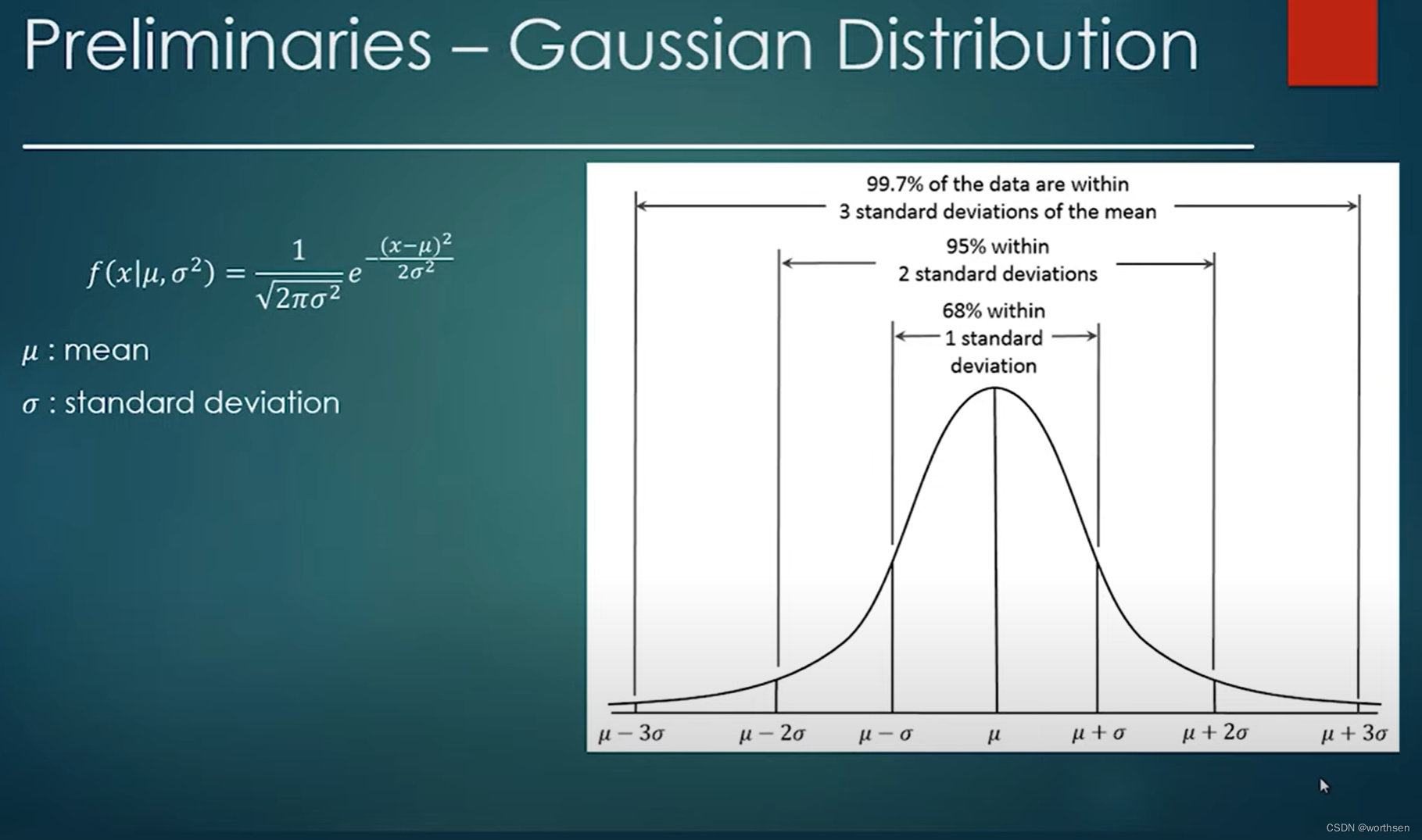
μ：mean 期望值
σ：标准差

n 维随机数组向量 $X=[X_1,X_2，...,X_n{]}^T$ 如下表示
$X\sim N(\mu ,\Sigma )$
n 维平均值向量 $\mu =E[X]=(E[X_1],E[X_2],...E[X_n])$

KF

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qRmpRK9C-1688134823023)(image-3.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cdOuvVlG-1688134823023)(image-4.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FSKgnVQU-1688134823023)(image-5.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NY5SFZeu-1688134823024)(image-6.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WRpTtZBq-1688134823024)(image-7.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ndfBxSmu-1688134823024)(image-8.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9LYsoBQ2-1688134823025)(image-9.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-15JDPr1n-1688134823025)(image-10.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YH4DZP8R-1688134823025)(image-11.png)]

EKF

UKF

徐亦达教授 Kalman Filter

徐亦达 Kalman Filter
徐亦达–香港浸会大学数学系教授
隐状态（隐变量），都是离散的。
预测（prediction）、观测、update。
数学中COV是协方差。

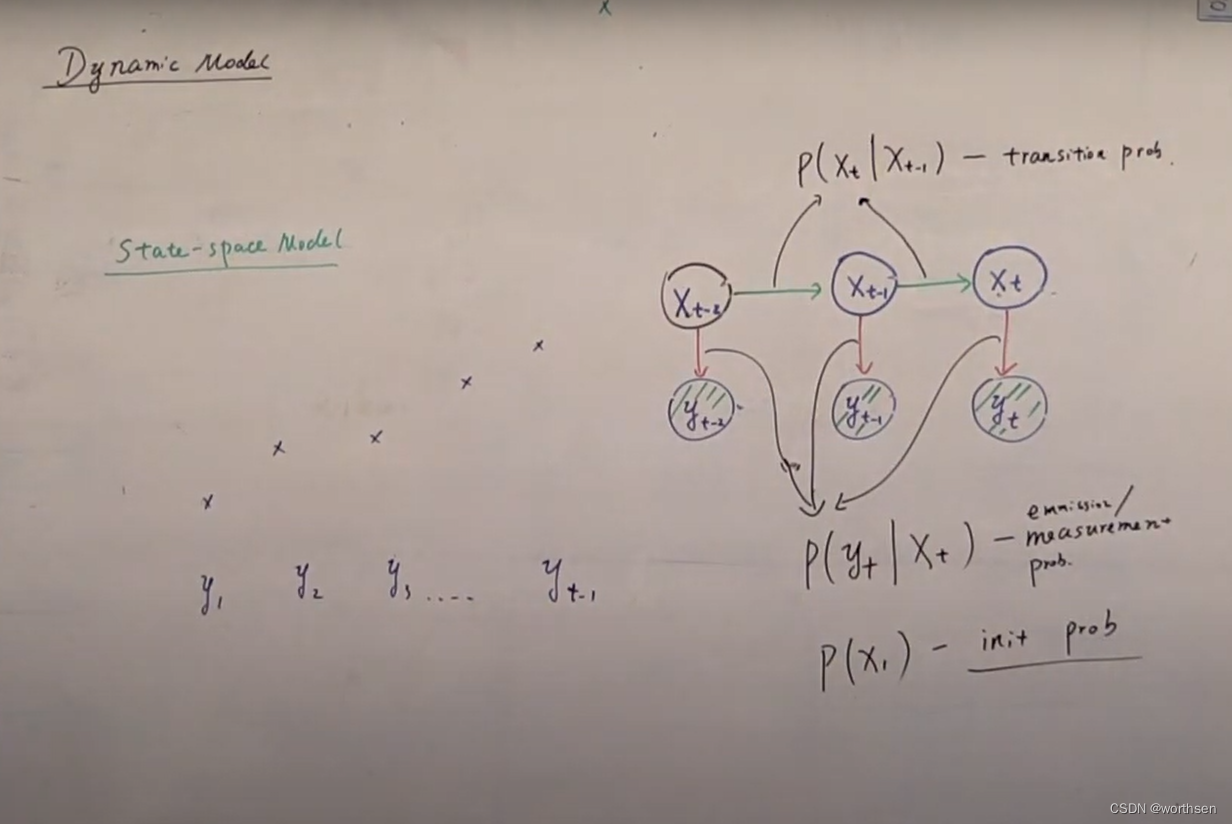
Jonathan kelly, assistant professor，aerospace studies

Machine Learning TV–Kalman Filter - Part 1
Machine Learning TV–Kalman Filter - Part 2

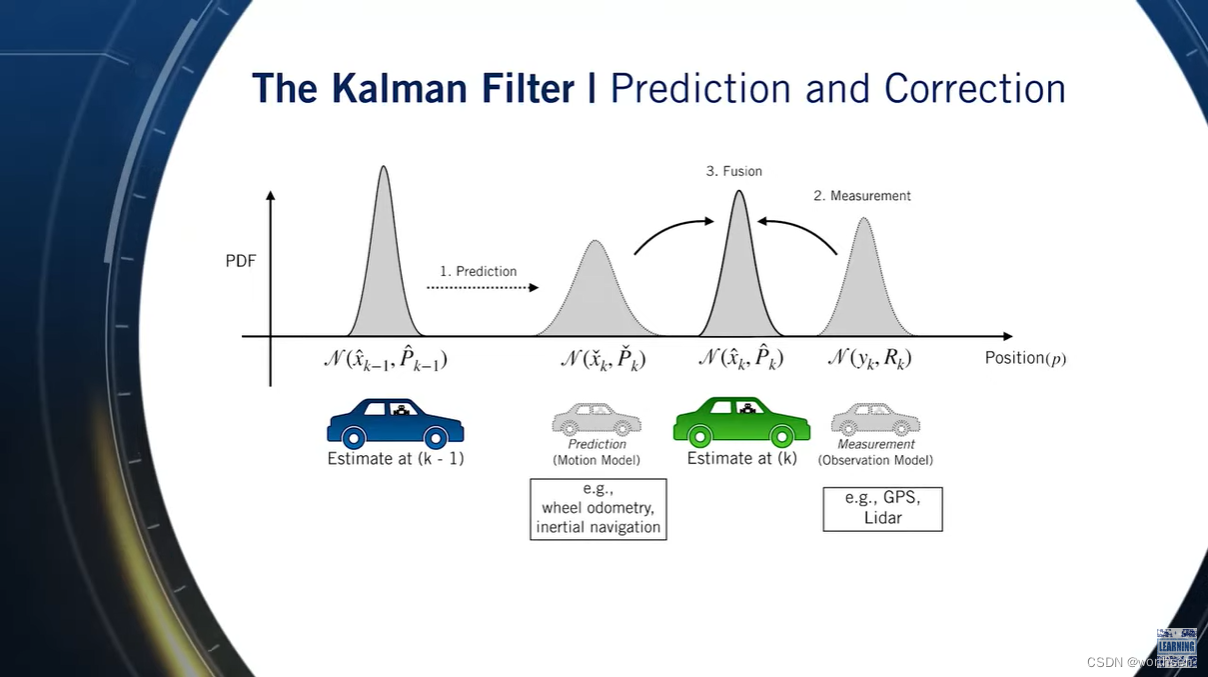
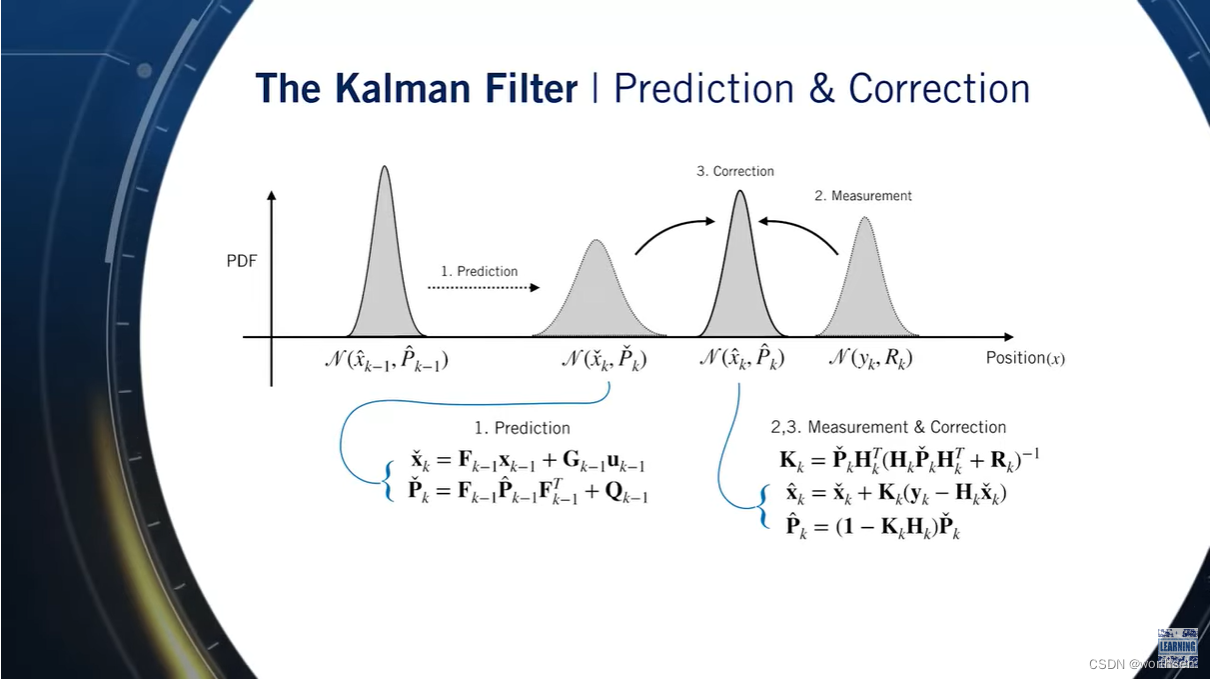
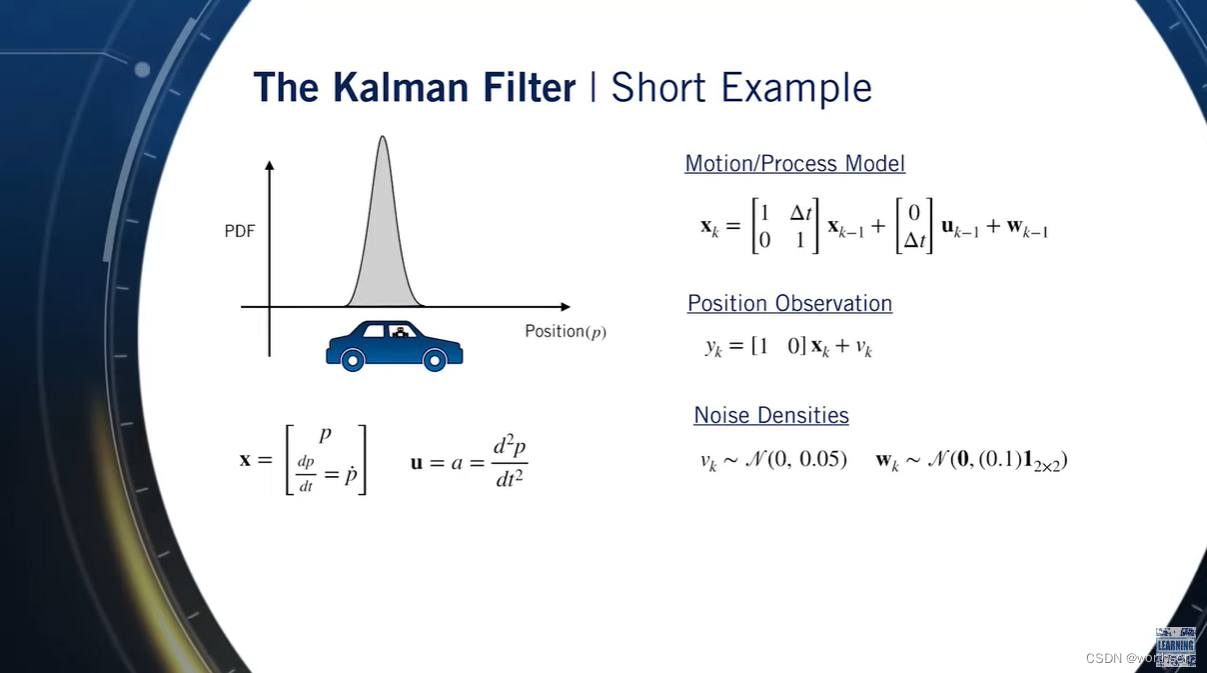
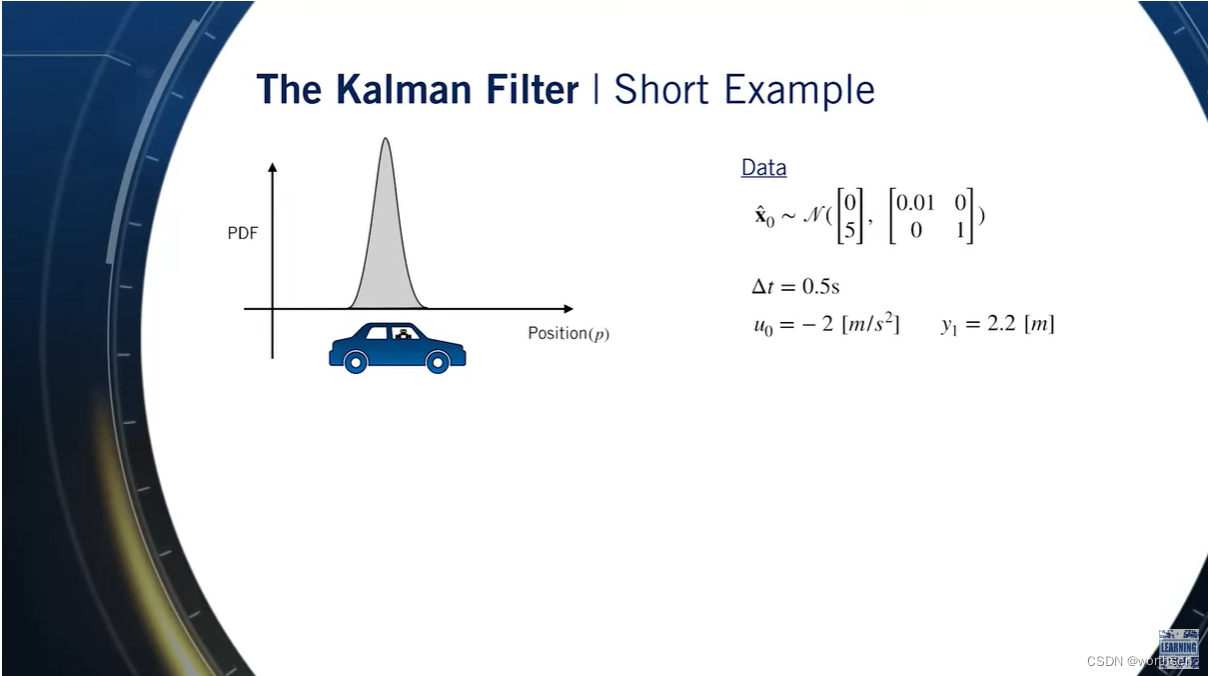
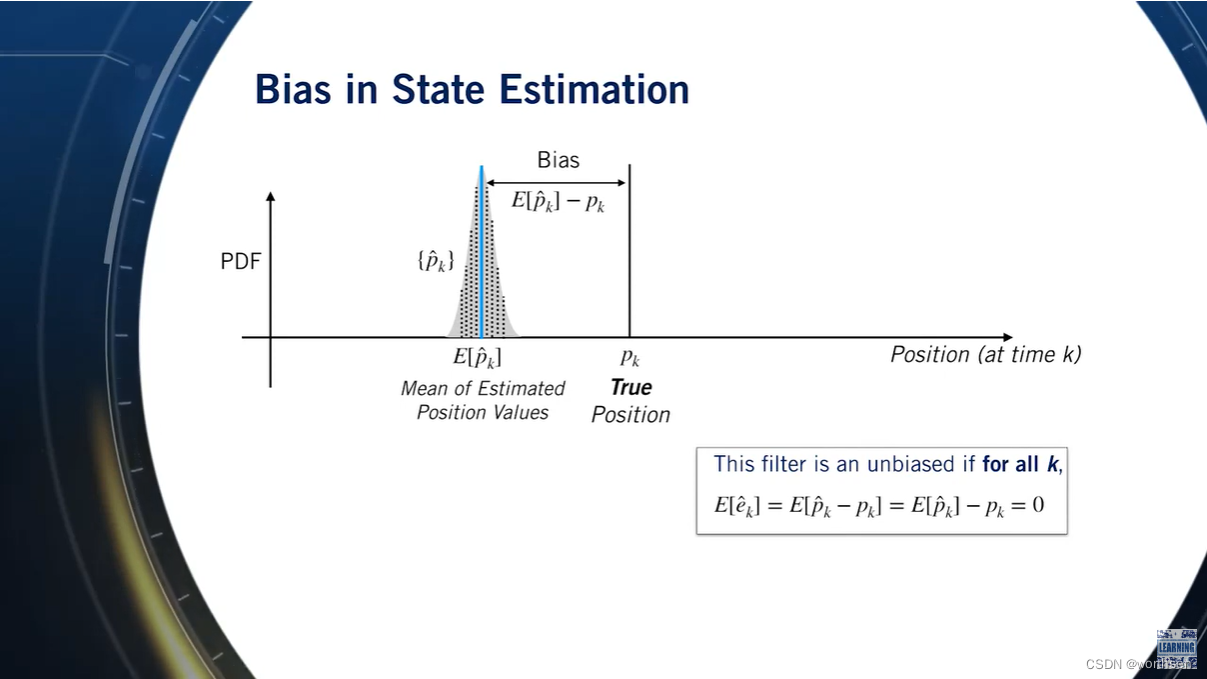
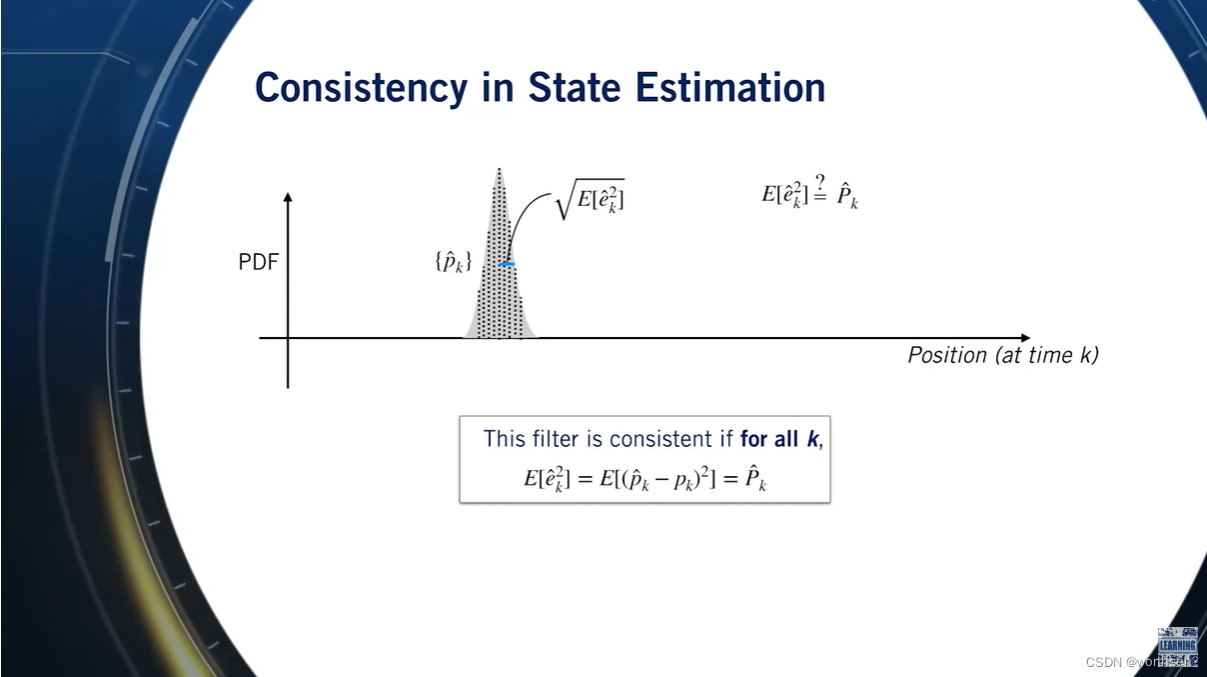
intermodalics–Real-Time Robotics: The Extended Kalman Filter

Part1: Real-Time Robotics: Before you start
Part2: Real-Time Robotics: How a Kalman Filter Can (not) Help
Part3: Real-Time Robotics: The Extended Kalman Filter

Slip, Drift, Noise, and … 滑动、漂移、噪声 …

机器人系统在很大程度上依赖传感器来提供有关环境和机器人本身的准确信息。然而，传感器并不完美，由于各种因素，往往会出现不准确的情况。这些误差可分为三大类:滑动、漂移和噪声。

• 滑移是指机器人的测量（或预期）位置或方向与其实际位置或方向之间的差异。滑动可能由多种因素引起，但最常见的是由于机械部件的磨损而导致机器人内部的滑动，以及由于抓取物体或驱动轮子时摩擦力的减少而导致机器人外部的滑动。
• 漂移是指传感器输出随时间逐渐、持续的变化。漂移可能由多种因素引起，例如温度变化、传感器老化或传感器融合、校准不良等。
• 噪声是指传感器输出中随机的、不需要的变化。噪声可能由多种因素引起，例如电气干扰、机械振动或传感器环境中的随机波动。

Jitter ?! 抖动

抖动是指获取传感器读数的时间变化，而不是读数本身的值。花一些时间研究下图：滑动、漂移和噪声会扭曲我们对实际值的观察，但抖动会扭曲我们对变化发生时间的估计。

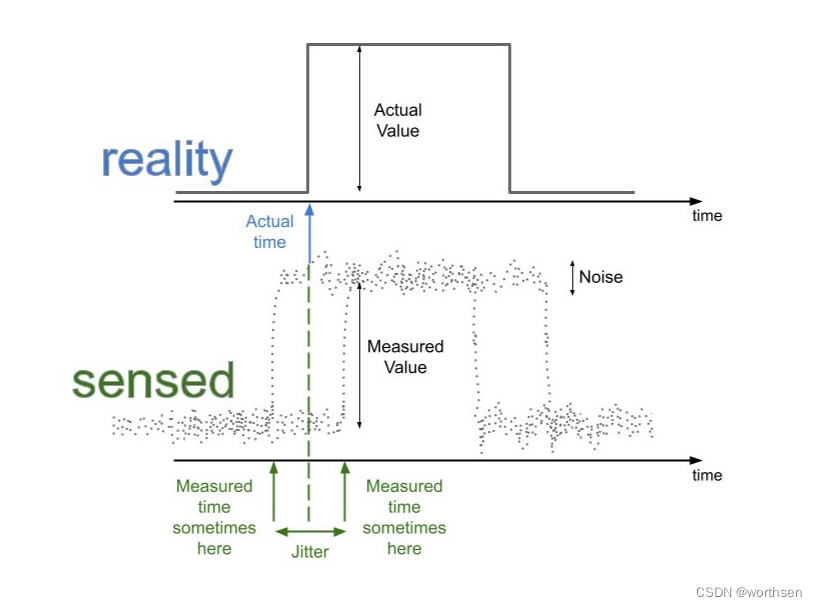
在这种情况下，抖动对于每个依赖于精确定时信息（因此称为“实时”）的实时控制算法来说都是一个问题，因为抖动会给生成的控制信号带来错误，无论它们的控制信号有多好。质量 ！

Addressing Jitter First 首先解决抖动问题

同步技术：

• 公共时钟信号：在这种技术中，多个传感器定期对其输入进行采样，使用公共电脉冲信号来协调它们的操作。因此，您可以保证每次测量都是同时完成的。
• 精确定时协议：IEEE 1588（精确时间协议）等协议可通过硬件和软件技术的组合，以高达微秒的高精度同步多个传感器和控制系统的操作。

如果无法直接解决抖动问题，从而导致测量不合节奏，则可以恢复测量获取传感器读数的时间。这需要具有三个重要功能的设置：

• 获取时间戳：许多传感器都有内置的实时时钟或时间戳，可用于记录获取读数的时间。
• 同步时钟：外部时钟信号，例如 GPS 信号或上述 IEEE 1588 协议，可用于同步传感器和控制系统的时钟，从而记录每次读数的准确时间。
• 重新对准：通过将每个传感器读数内插或外推到该时刻，将测量值重新对准到单个时刻的方法。

Eliminating Jitter in C/C++ 借助高效语言消除抖动

• Xenomai：是一个实时操作系统（RTOS），它提供了一组用于在 Linux 上构建实时应用程序的库和工具。它旨在支持广泛的实时应用，包括控制系统、数据采集系统和嵌入式系统。
• Orocos Real-Time Toolkit (RTT)：是一个用于在 Linux 上构建实时控制系统的 C++ 库。它是 Orocos 项目的一部分，该项目是一组用于构建机器人应用程序的工具和库。
• Rock Robotics：与 Orocos RTT 和 ROS 集成，并包含一个Stream Aligner 组件，用于根据时间戳对齐数据流。
• Real-Time Linux (PREEMPT_RT)：专门为实现基于 EKF 的同步定位和建图 (SLAM) 算法而设计的库。
• Simulink Coder：从 Simulink® 模型、Stateflow® 图和 MATLAB® 函数生成并执行 C 和 C++ 代码。生成的源代码可用于实时和非实时应用，包括仿真加速、快速原型设计和硬件在环测试。

What is the Kalman Filter & How Does It Work? 什么是卡尔曼滤波器及其工作原理？

卡尔曼滤波器是一种实时最优估计算法，它使用一系列测量来估计系统的状态。它由鲁道夫·卡尔曼 (Rudolf Kalman) 在 20 世纪 60 年代开发，广泛应用于从机器人到金融等领域。卡尔曼滤波器的工作原理是将多个测量值组合在一起，生成比任何单个测量值更准确的估计值。

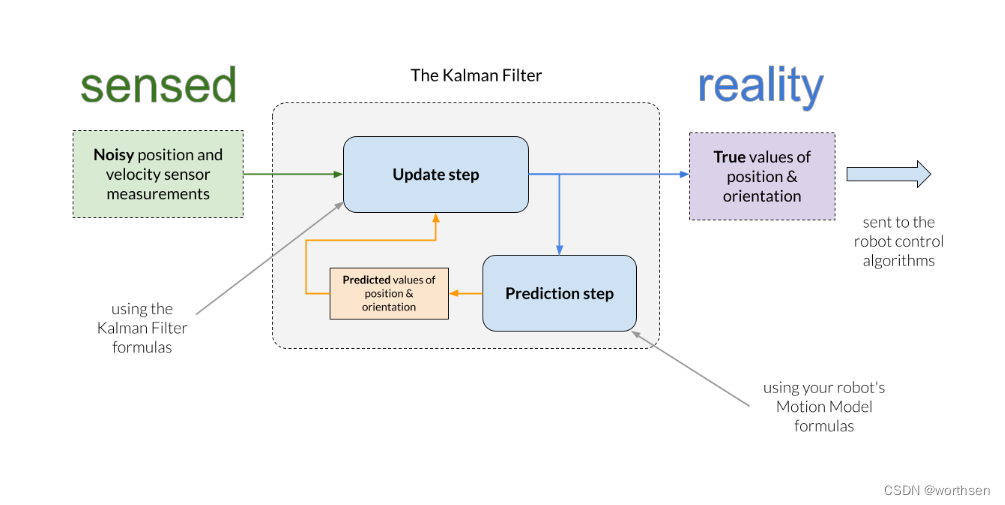
要使用卡尔曼滤波器，需要拥有一个具有以下属性的系统：

• 动态或静态系统：卡尔曼滤波器最初设计用于估计动态系统的状态。然而，您也可以使用它来估计不移动的静态系统的状态。
• 线性系统：卡尔曼滤波器只能用于线性系统，这意味着系统动力学可以通过一组线性微分方程来描述。
• 连续时间或离散时间系统：卡尔曼滤波器可用于连续时间和离散时间系统。对于连续时间系统，滤波器通常使用连续时间状态空间模型和微分方程来实现。对于离散时间系统，滤波器通常使用离散时间状态空间模型和差分方程来实现。
• 已知的系统动力学：卡尔曼滤波器需要系统动力学模型，这意味着您必须充分了解系统的行为方式以及系统如何受到外部输入和内部过程的影响。
• 正确测量的输入：卡尔曼滤波器使用系统的测量来估计系统的真实状态。这些测量必须实时可用，并且必须足够准确，以提供有关系统状态的有用信息。
• 已知测量噪声：卡尔曼滤波器需要有关测量过程中的噪声的信息，该信息用于衡量滤波器估计中测量的重要性。这种噪声可能是由多种因素造成的，包括测量误差、传感器噪声和环境干扰，并被假定为高斯白噪声。

卡尔曼滤波器非常适合测量简单的线性系统，例如温度读数、电流读数或光强度。但我们不能用它来测量机器人的位置和速度，因为不幸的是这些几乎从来都不是线性的……

Revisiting the Kalman Filter 重新审视卡尔曼滤波器

扩展卡尔曼滤波器 (EKF) 是标准卡尔曼滤波器的必要扩展，可用于非线性系统。例如，在移动机器人的情况下，机器人的位置、速度和加速度可以建模为非线性系统，因为机器人的运动不一定是线性的。
在卡尔曼滤波器中，$系统的状态$ 由一组变量表示，这些变量是根据一组 $测量$ 值和 $预测的系统状态$ 进行估计的。因此本质上，卡尔曼滤波器总是会 $预测$ 系统的状态如何随时间变化，并根据这些测量和预测来 $计算（更新）$系统的当前状态。

In the Kalman filter, the $stateofthesystem$ is represented by a set of variables that are estimated based on a set of $measurements$ and the $predictedsystemstate$ predicted system state. Therefore in essence, the Kalman filter will always $predict$ how the state of the system changes over time, and $calculate(update)$ the current state of the system based on these measurements and the prediction.

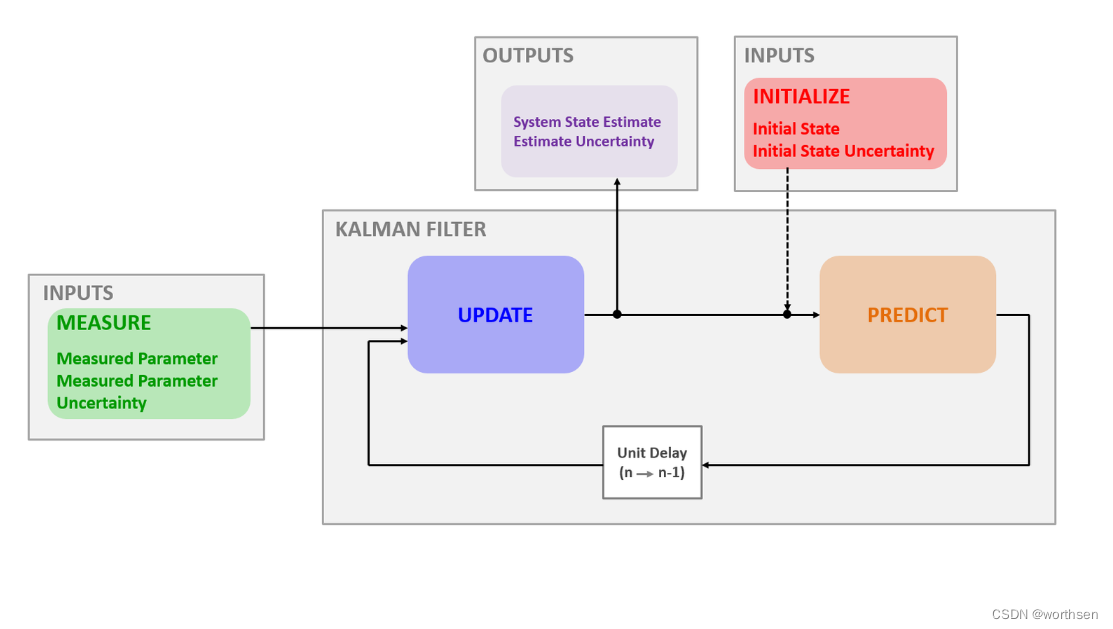
应用于移动机器人时，任何给定时间的 系统状态估计（卡尔曼滤波器的输出）可能包括机器人在 x 和 y 方向上的位置、旋转和速度。因此，这些是我们想要在每个时间步长中估计（即计算）的值。它们是通过 更新 步骤计算的，该步骤根据 预测 （使用过程模型）和 测量（使用测量模型）计算机器人的当前位置、旋转和速度。

对于简单的移动机器人，例如差动驱动机器人，我们可以使用三个变量来描述其状态：x 位置 (x)、y 位置 (y) 和方向 (θ)，如图所示。

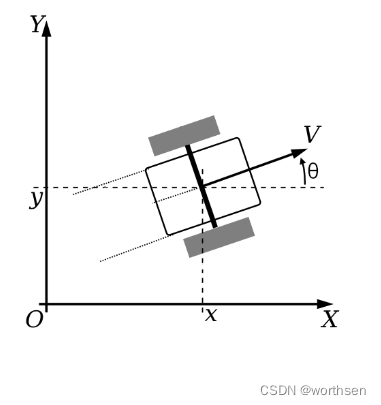
我们的过程模型是在给定机器人在 t 处的位置、方向、线速度 v 和旋转速度 ω 的情况下预测机器人在t + 1处的下一个位置和方向的公式：
x(t+1) = x(t) + v(t) * cos ( θ(t) ) * Δt
y(t+1) = y(t) + v(t) * sin ( θ(t) ) * Δt
θ(t+1) = θ(t) + ω(t) * Δt

The Extended Kalman Filter

增强卡尔曼滤波器，先将非线性系统进行线性化，再做处理，这里要用到雅可比矩阵。该矩阵由非线性函数相对于状态变量的偏导数组成。有一些开源库可以在给定系统模型的情况下计算雅可比矩阵。

一旦我们有了雅可比矩阵 (J)，我们就可以用它来创建线性过程模型：
$$\begin{array}{rl}f(X)& \approx f(\hat{X})+J\ast (X-\hat{X})\\ & =\underline{J}\ast X+\underline{[f(\hat{X})-J\ast \hat{X}]}\\ & =\underline{a}\ast X+\underline{b}\end{array}$$

在第一个方程中，f(x) 是非线性模型，它由右侧的线性化估计来近似 (≈)。该估计值由 x̂ 处的状态实际值加上雅可比行列式 J（x̂ 处 f(x) 的导数）以及线性化估计值与状态实际值 (𝘅 - x̂) 之间的差值组成。该方程表示一条 ( y = ax + b )形式的直线，这使其成为线性模型。

Extended Kalman Filtering with Python and C++ 使用 Python 和 C++ 扩展卡尔曼滤波

有多个开源 C++ 和 Python 库可用于实现扩展卡尔曼滤波器 (EKF)。一些例子包括：
在 C++ 中：

• Eigen：一个线性代数库，提供实现 EKF 所需的许多函数，包括矩阵运算、分解和求解器。
• Boost.Odeint：一个提供求解常微分方程工具的库，可用于实现 EKF 的预测步骤。
• Kalman：基于 Eigen3 的流行的纯头文件 C++ 库，其中包括扩展卡尔曼滤波器 (EKF)、平方根扩展卡尔曼滤波器 (SR-EKF)、无迹卡尔曼滤波器 (UKF) 和平方根无迹卡尔曼滤波器 (SR-UKF) 。
• Kalman-cpp：仅限 Microsoft Windows，具有与上述 Kalman 类似的支持，但基于 blas 和 lapack。

在Python中：

• SciPy：一个提供优化、集成和插值工具的库，可用于实现 EKF 的预测步骤。
• PyKalman：提供卡尔曼滤波器和无味卡尔曼滤波器实现的库
• FilterPy：FilterPy 是一个 Python 库，它实现了许多贝叶斯滤波器，最著名的是扩展和无迹卡尔曼滤波器。它托管在github上。

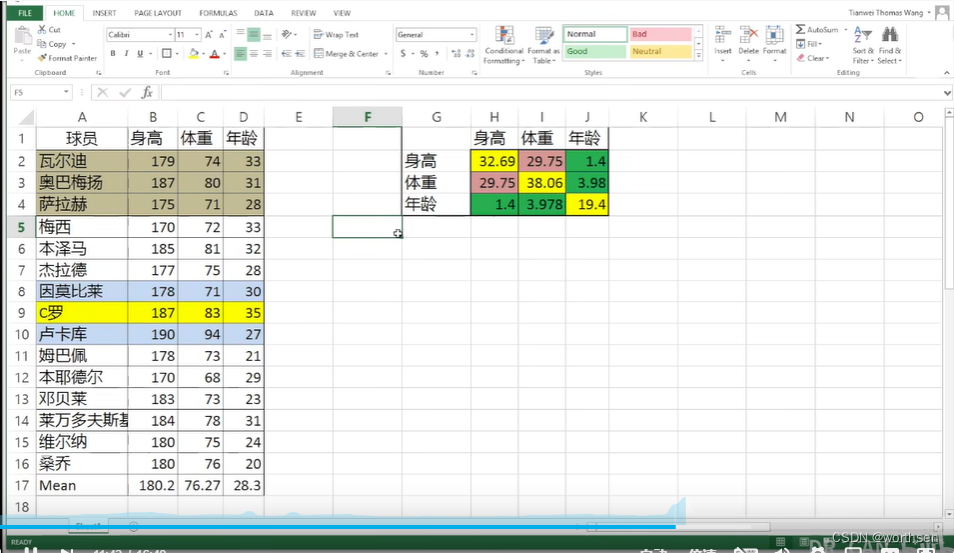
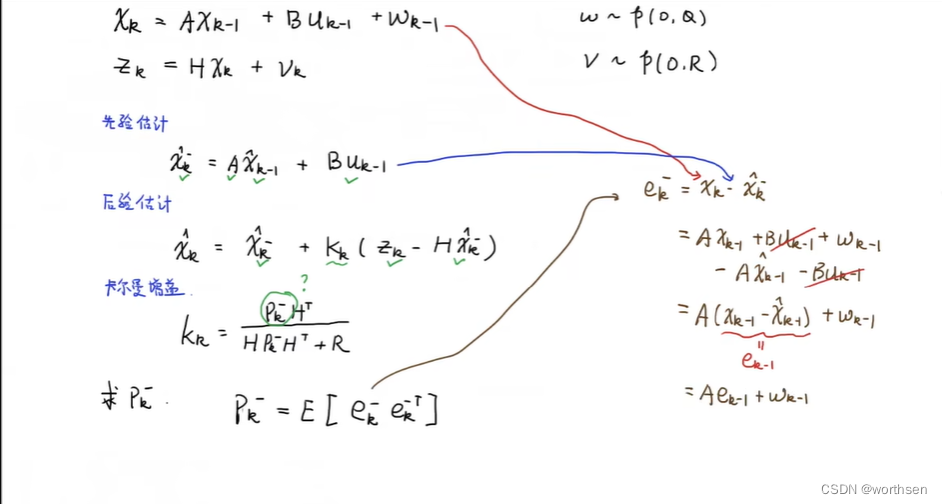
DR_CAN 博士–卡尔曼滤波器详细数学推导

DR_CAN 博士–卡尔曼滤波器详细数学推导

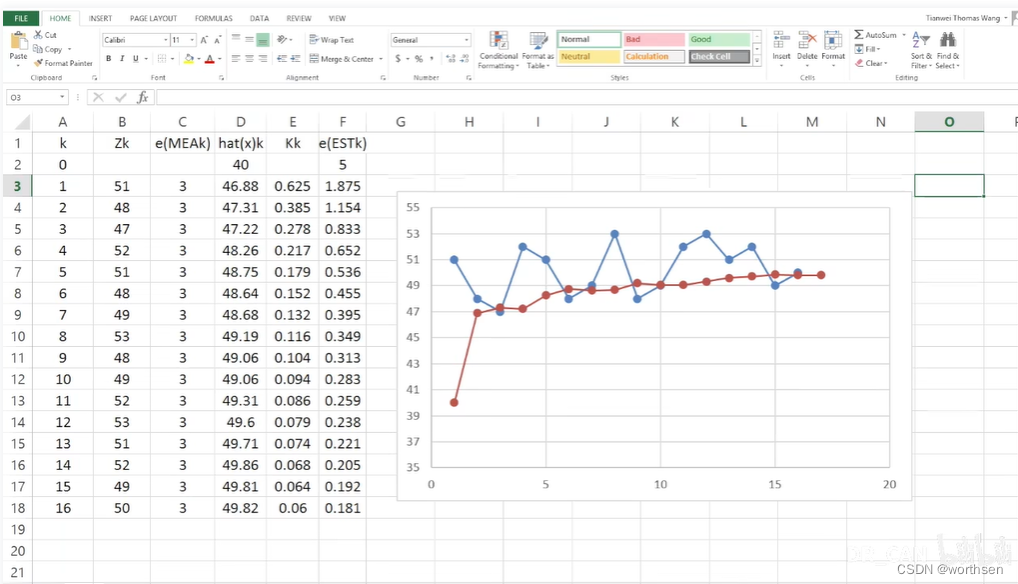
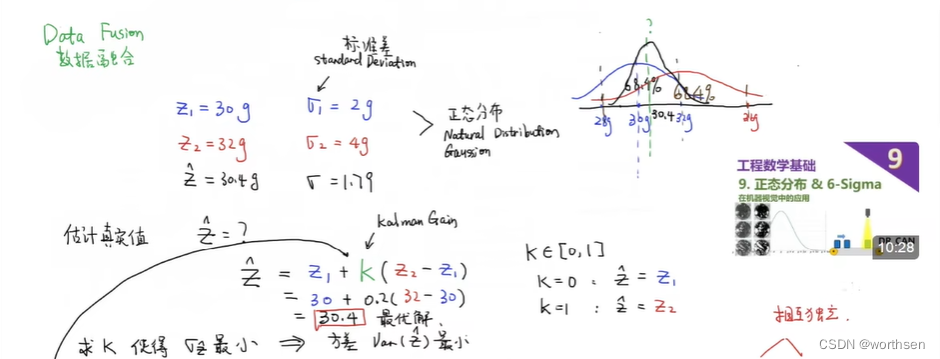
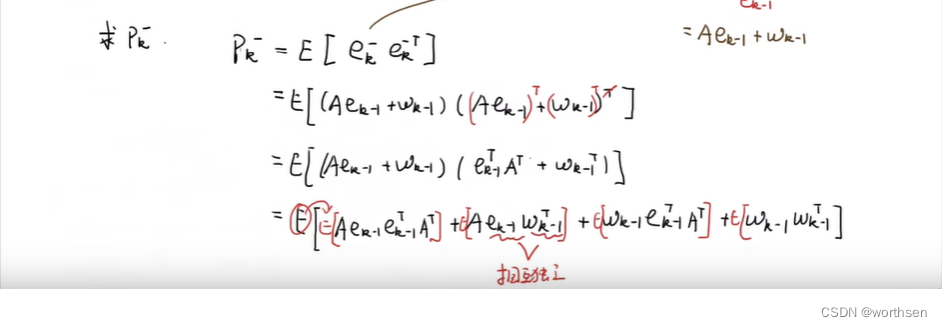
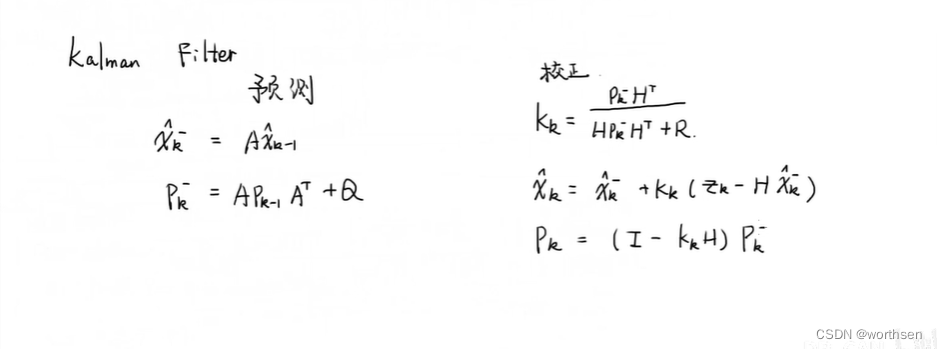
古月居–卡尔曼滤波的理解、推导和应用

古月居–卡尔曼滤波的理解、推导和应用

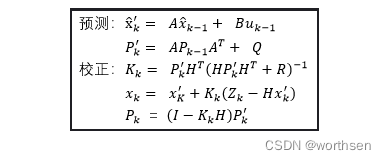
公式（一）：计算预测状态值
公式（二）：计算预测值和真实值之间的预测误差协方差矩阵
公式（三）：在公式一和公式二的条件下，求得卡尔曼增益
公式（四）：计算估计值
公式（五）：计算估计值和真实值之间的误差协方差矩阵

import numpy as np
import matplotlib.pyplot as plt

delta_t = 0.1                               # 每秒钟采一次样
end_t = 7                                   # 时间长度
time_t = end_t * 10                         # 采样次数
t = np.arange(0, end_t, delta_t)            # 设置时间数组

u = 1                                       # 定义外界对系统的作用 加速度
x = 1 / 2 * u * t ** 2                      # 实际真实位置

v_var = 1                                   # 测量噪声的方差
# 创建高斯噪声，精确到小数点后两位
v_noise = np.round(np.random.normal(0, v_var, time_t), 2)

X = np.mat([[0], [0]])                      # 定义预测优化值的初始状态
v = np.mat(v_noise)                         # 定义测量噪声
z = x + v                                   # 定义测量值（假设测量值=实际状态值+噪声）
A = np.mat([[1, delta_t], [0, 1]])          # 定义状态转移矩阵
B = [[1 / 2 * (delta_t ** 2)], [delta_t]]   # 定义输入控制矩阵
P = np.mat([[1, 0], [0, 1]])                # 定义初始状态协方差矩阵
Q = np.mat([[0.001, 0], [0, 0.001]])        # 定义状态转移(预测噪声)协方差矩阵
H = np.mat([1, 0])                          # 定义观测矩阵
R = np.mat([1])                             # 定义观测噪声协方差
X_mat = np.zeros(time_t)                    # 初始化记录系统预测优化值的列表

for i in range(time_t):
    # 预测
    X_predict = A * X + np.dot(B, u)        # 估算状态变量
    P_predict = A * P * A.T + Q             # 估算状态误差协方差
    # 校正
    K = P_predict * H.T / (H * P_predict * H.T + R)     # 更新卡尔曼增益
    X = X_predict + K * (z[0, i] - H * X_predict)       # 更新预测优化值
    P = (np.eye(2) - K * H) * P_predict                 # 更新状态误差协方差
    # 记录系统的预测优化值
    X_mat[i] = X[0, 0]

plt.rcParams['font.sans-serif'] = ['SimHei']    # 设置正常显示中文
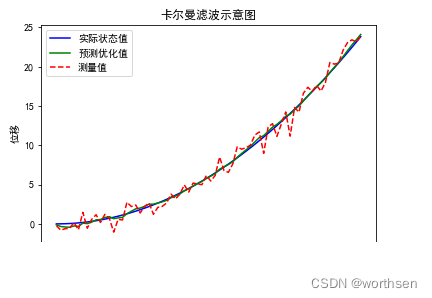
plt.plot(x, "b", label='实际状态值')             # 设置曲线数值
plt.plot(X_mat, "g", label='预测优化值')
plt.plot(z.T, "r--", label='测量值')
plt.xlabel("时间")                               # 设置X轴的名字
plt.ylabel("位移")                               # 设置Y轴的名字
plt.title("卡尔曼滤波示意图")                     # 设置标题
plt.legend()                                    # 设置图例
plt.show()                                      # 显示图表

3 EKF 公式

from wiki–Extended Kalman filter

参考

1、wiki–Extended Kalman filter
2、wiki–Kalman filter
3、Timothy. Barfoot, “State estimation for Robotics: A Matrix Lei Group Approach”, 2016.
4、機器人學：多軸旋翼機 Lec11 - 卡爾曼濾波器、擴展卡爾曼濾波器、無損卡爾曼濾波 KF、EKF、UKF
5、高翔–SLAM中的EKF，UKF，PF原理简介
6、扩展卡尔曼滤波（EKF）算法详细推导及仿真（Matlab）
7、卡尔曼滤波
8、卡尔曼滤波原理二：扩展卡尔曼
9、扩展卡尔曼滤波详解
10、扩展卡尔曼滤波算法及仿真实例
11、卡尔曼滤波-EKF
12、ardupilot–Extended Kalman Filter (EKF)
13、sciencedirect：
https://www.sciencedirect.com/topics/engineering/extended-kalman-filter
https://www.sciencedirect.com/topics/computer-science/extended-kalman-filter
14、SOC–使用扩展卡尔曼滤波（EKF）估计电池SOC（附MATLAB程序及详解）part1主函数篇
15、SOC–BMS（电池管理系统）第四课 ——核心！！！SOC算法开发
16、【统计】z分位数&标准正态分布表（z-table）
17、标准正态分布表_机器学习
18、概率论的学习和整理7：期望和方差，回到随机实验本身去理解
19、概率论的学习和整理12： 正态分布
20、概率论的学习和整理13–方差和协方差（未完成）
21、徐亦达 Kalman Filter
22、在 Simulink 中使用扩展卡尔曼滤波器
23、Machine Learning TV–Kalman Filter - Part 1
24、Machine Learning TV–Kalman Filter - Part 2
25、An Optimal State Estimator | Understanding Kalman Filters, Part 3
26、Kalman滤波通俗理解+实际应用
27、DR_CAN 博士–卡尔曼滤波器详细数学推导
28、贝叶斯滤波与卡尔曼滤波第十四讲 无迹卡尔曼滤波
29、卡尔曼滤波：入门视频推荐与学习笔记
30、Extended Kalman Filter Tutorial
31、Tutorial: The Kalman Filter
32、扩展卡尔曼滤波(EKF)代码实战
33、JuliaGNSS / KalmanFilters
34、Extended Kalman Filter: How to Implement in C++ with Eigen
35、Real-Time Robotics: The Extended Kalman Filter
36、kalmanfilter.net
37、Alan Zucconi–The Extended Kalman Filter
38、卡尔曼滤波原理详解及系统模型建立（simulink）
39、优化与算法
40、古月居–卡尔曼滤波的理解、推导和应用
41、卡尔曼滤波 KF | 扩展卡尔曼滤波 EKF （思路流程和计算公式）