🤵‍♂️ 个人主页：@艾派森的个人主页

✍🏻作者简介：Python学习者
🐋 希望大家多多支持，我们一起进步！😄
如果文章对你有帮助的话，
欢迎评论 💬点赞👍🏻 收藏 📂加关注+

喜欢大数据分析项目的小伙伴，希望可以多多支持该系列的其他文章

大数据分析案例合集
大数据分析案例-基于随机森林算法预测人类预期寿命
大数据分析案例-基于随机森林算法的商品评价情感分析
大数据分析案例-用RFM模型对客户价值分析(聚类)
大数据分析案例-对电信客户流失分析预警预测
大数据分析案例-基于随机森林模型对北京房价进行预测
大数据分析案例-基于RFM模型对电商客户价值分析
大数据分析案例-基于逻辑回归算法构建垃圾邮件分类器模型
大数据分析案例-基于决策树算法构建员工离职预测模型
大数据分析案例-基于KNN算法对茅台股票进行预测
大数据分析案例-基于多元线性回归算法构建广告投放收益模型
大数据分析案例-基于随机森林算法构建返乡人群预测模型
大数据分析案例-基于决策树算法构建金融反欺诈分类模型

1.项目背景

2.项目简介

2.1项目说明

2.2数据说明

2.3技术工具

3.算法原理

4.项目实施步骤

4.1理解数据

4.2数据预处理

4.3探索性数据分析

4.3.1破产比例情况

4.3.2相关关系可视化

4.3.3正相关可视化

4.3.4负相关可视化

4.4特征工程

4.5模型构建

4.6模型评估

4.7特征重要性评分

4.8模型预测

5.实验总结

源代码

1.项目背景

破产预测一直是企业金融研究和实践中的一个重要课题。在经济不稳定和竞争激烈的商业环境下，准确预测企业是否面临破产风险对于投资者、债权人、供应商和管理层来说都具有重要意义。

过去，破产预测主要依靠传统的统计模型和人工经验。然而，随着机器学习的发展，基于算法的预测模型逐渐成为破产预测研究领域的新趋势。这些算法可以利用大量的企业数据，自动学习和识别与破产相关的模式和特征，从而提高预测的准确性和可靠性。

LightGBM是一种基于梯度提升决策树的机器学习算法，具有训练速度快、高效、准确性好等优点。它在处理大规模数据集和高维特征时表现出色，并且能够处理各种类型的数据。因此，将LightGBM算法应用于破产预测模型的构建中具有一定的优势和潜力。

通过基于LightGBM算法构建公司破产预测模型，可以实现以下目标：

提高破产预测的准确性：LightGBM算法可以自动学习和捕捉与企业破产相关的复杂模式和特征，从而提高预测的准确性。
实时监测和风险管理：建立一个可实时监测企业破产风险的模型，可以帮助投资者、债权人和供应商及时调整风险策略，减少潜在损失。
支持决策制定：破产预测模型可以为管理层提供有关企业财务健康状况的重要信息，帮助其制定合理的决策和战略，以维护企业的稳定发展。

综上所述，基于LightGBM算法构建公司破产预测模型具有重要的研究价值和实际应用意义。它可以提供一种更准确、高效和可靠的方法来评估企业破产风险，为相关利益相关方提供决策支持，促进企业的可持续发展。

2.项目简介

2.1项目说明

本项目旨在通过对以往公司破产数据进行数据分析、数据挖掘来找出影响破产的因素，以及使用机器学习算法构建公司破产预测模型，实时监测企业破产风险，帮助企业减少潜在损失，维护企业健康稳定发展。

2.2数据说明

本数据集来源于kaggle，原始数据集共有6819条，共96个变量，各变量具体含义解释如下：

（Y = 输出特征，X = 输入特征）

Y - 破产？：类别标签，是否破产
X1 - 利息和利息前折旧前的 ROA(C)：总资产回报率 (C)
X2 - 利息前 ROA(A) 和税后百分比：总资产回报率 (A)
X3 - ROA (B) 税后利息和折旧前：总资产回报率(B)
X4 - 营业毛利率：毛利润/净销售额
X5 - 已实现销售毛利率：已实现毛利润/净销售额
X6 - 营业利润率：营业收入/净销售额
X7 - 税前净利率：税前收入/净销售额
X8 - 税后净利率：净利润/净销售额
X9 - 非业收支/收入：营业外净收入比率
X10 - 连续利率（税后）：净利润-不包括处置损益/净销售额
X11 - 营业费用率：营业费用/净销售额
X12 - 研发费用率：（研发费用）/净销售额
X13 - 现金流量率：经营/流动负债产生的现金流量
X14 - 有息债务利率：有息债务/股权
X15 - 税率 (A)：有效税率
X16 - 每股净值 (B)：账面价值每股(B)
X17 - 每股净值(A)：每股账面价值(A)
X18 - 每股净值(C)：每股账面价值(C)
X19 - 过去四个季度的持续每股收益：每股收益-净利润
X20 - 每股现金流
X21 - 每股营业收入（元 ¥）：每股销售额
X22 - 每股营业利润（元 ¥）：每股营业收入
X23 - 每股税前净利润（元 ¥）：税前每股收益
X24 - 已实现销售总额利润增长率
X25 - 营业利润增长率：营业收入增长率
X26 - 税后净利润增长率：净利润增长率
X27 - 常规净利润增长率：税后持续营业收入增长率
X28 - 连续净利润增长率：净利润- 剔除处置损益增长
X29 - 总资产增长率：总资产增长
X30 - 净值增长率：总权益增长
X31 - 总资产回报率增长率：总资产增长回报率
X32 - 现金再投资百分比：现金再投资比率
X33 - 流动比率
X34 - 速动比率：酸测试

X35- 利息支出比率：利息支出/总收入
X36 - 总债务/总净值：总负债/股本比率
X37 - 债务比率 % ：负债/总资产
X38 - 净值/资产：权益/总资产
X39 - 长期资金适宜比率（A）：（长期负债+权益）/固定资产
X40 - 借款依存度：有息债务成本
X41 - 或有负债/净值：或有负债/股本
X42 - 营业利润/实收资本：营业收入/资本
X43 - 税前净利润/实收资本：税前收入/资本
X44 - 存货及应收账款/净值：（存货+应收账款）/权益
X45 - 总资产周转率
X46 - 应收账款周转率
X47 - 平均收款天数：应收账款周转天数
X48 - 存货周转率（次）
X49 - 固定资产周转率频率
X50 - 净资产周转率（次）：股权周转率
X51 - 人均收入：每个员工的销售额
X52 - 人均营业利润：每个员工的营业收入
X53 - 人均分配率：每个员工的固定资产
X54 - 营运资金占总额资产
X55 - 速动资产/总资产
X56 - 流动资产/总资产
X57 - 现金/总资产
X58 - 速动资产/流动负债
X59 - 现金/流动负债
X60 - 流动负债与资产之比
X61 - 营运资金与负债之比
X62 - 库存/营运资金
X63 - 库存/流动负债
X64 - 流动负债/负债
X65 - 营运资金/权益
X66 - 流动负债/权益
X67 - 流动资产长期负债
X68 - 留存收益与总资产之比
X69 - 总收入/总支出
X70 - 总支出/资产
X71 - 流动资产周转率：流动资产与销售额之比
X72 - 快速资产周转率比率：快速资产销售额
X73 - 营运资本周转率：营运资本销售额
X74 - 现金周转率：现金与销售收入之比
X75 - 现金流量与销售收入之比

X76 - 固定资产与资产之比

X77- 流动负债与负债之比

X78 - 流动负债与权益之比

X79 - 权益与长期负债之比
X80 - 现金流与总资产之比
X81 -负债现金流量
X82 - 首席财务官与资产之比
X83 - 股本现金流量
X84 - 流动负债与流动资产之比
X85 - 负债-资产标志：如果总负债超过总资产则为 1，否则为 0
X86 - 净利润与总资产之比
X87 - 总资产GNP 价格
X88 - 无信贷区间
X89 - 销售毛利
X90 - 股东权益净收入
X91 - 权益负债
X92 - 财务杠杆率 (DFL)
X93 - 利息覆盖率（利息支出与息税前利润之比）
X94 - 净利润标志：如果过去两年净利润为负，则为 1，否则为 0
X95 - 权益与负债之比

2.3技术工具

Python版本:3.9

代码编辑器：jupyter notebook

3.算法原理

LightGBM算法基本原理

GBDT算法的基本思想是把上一轮的训练残差作为下一轮学习器训练的输入，即每一次的输入数据都依赖于上一次训练的输出结果。因此，这种训练迭代过程就需要多次对整个数据集进行遍历，当数据集样本较多或者维数过高时会增加算法运算的时间成本，并且消耗更高的内存资源。

而XGBoost算法作为GBDT的一种改进，在训练时是基于一种预排序的思想来寻找特征中的最佳分割点，这种训练方式同样也会导致内存空间消耗极大，例如算法不仅需要保存数据的特征值，还需要保存特征排序的结果；在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的代价大，特别是当数据量级较大时，这种方式会消耗过多时间。

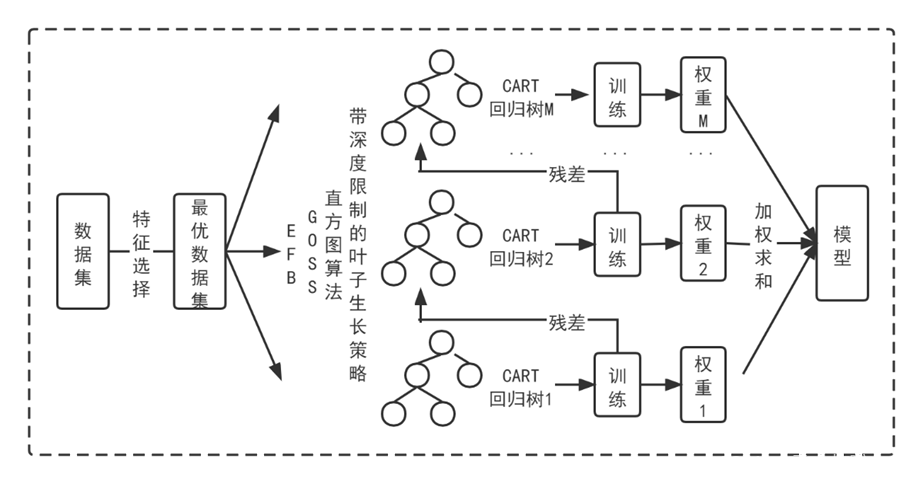
为了对这些问题进行优化，2017年微软公司提出了LightGBM算法（Light Gradient Boosting Machine），该算法也是基于GBDT算法的改进，，但相较于GBDT、XGBoost算法，LightGBM算法有效地解决了处理海量数据的问题，在实际应用中取得出色的效果。LightGBM算法主要包括以下几个特点：直方图算法（寻找最佳分裂点、直方图差加速）、Leaf-wise树生长策略、GOSS、EFB、支持类别型特征、高效并行以及Cache命中率优化等。

（1）直方图Histogram算法（减少大量计算与内存占用）

XGBoost算法在进行分裂时需要预先对每一个特征的原始数据进行预排序，而直方图Histogram算法则是对特征的原始数据进行“分桶#bin”，把数据划分到不同的离散区域中，再对离散数据进行遍历，寻找最优划分点。这里针对特征值划分的每一个“桶”有两层含义，一个是每个“桶”中样本的数量；另一个是每个“桶”中样本的梯度和（一阶梯度和的平方的均值等价于均方损失）。

可以看出，通过直方图算法可以让模型的复杂度变得更低，并且特征“分桶”后仅保存了的离散值，大大降低内存的占用率。其次，这种“分桶”的方式从某种角度来看相当于对模型增加了正则化，可以避免模型出现过拟合。

值得注意的是，直方图算法是使用了bin代替原始数据，相当于增加了正则化，这也意味着有更多的细节特征会被丢弃，相似的数据可能被划分到相同的桶中，所以bin的数量选择决定了正则化的程度，bin越少惩罚越严重，过拟合的风险就越低。

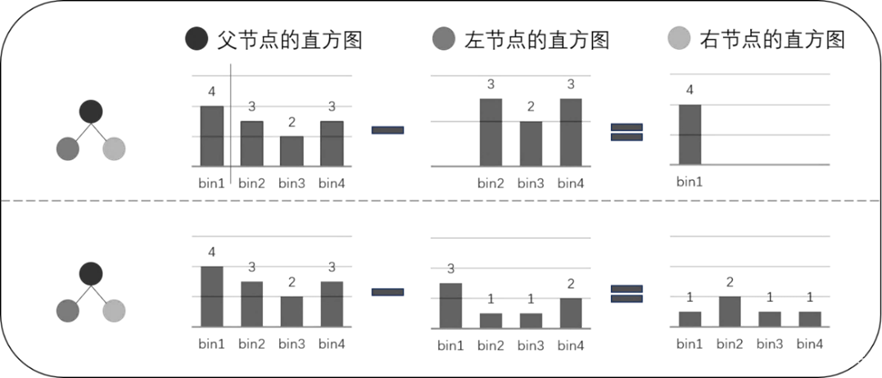
图 2 6 直方图作差

另外，在LightGBM直方图算法中还包括一种直方图作差优化，即LightGBM在得到一个叶子的直方图后，能够通过直方图作差的方式用极小的代价得到其兄弟叶子的直方图，如上图所示，当得到某个叶子的直方图和父节点直方图后，另一个兄弟叶子直方图也能够很快得到，利用这种方式，LightGBM算法速度得到进一步提升。

（2）带深度限制的Leaf-wise的叶子生长策略（减少大量计算、避免过拟合）

GBDT与XGBoost模型在叶子生长策略上均采用按层level-wise分裂的方式，这种方式在分裂时会针对同一层的每一个节点，即每次迭代都要遍历整个数据集中的全部数据，这种方式虽然可以使每一层的叶子节点并行完成，并控制模型的复杂度，但也会产生许多不必要搜索或分裂，从而消耗更多的运行内存，增加计算成本。

而LightGBM算法对其进行了改进，使用了按叶子节点leaf-wise分裂的生长方式，即每次是对所有叶子中分裂增益最大的叶子节点进行分裂，其他叶子节点则不会分裂。这种分裂方式比按层分裂会带来更小的误差，并且加快算法的学习速度，但由于没有对其他叶子进行分裂，会使得分裂结果不够细化，并且在每层中只对一个叶子不断进行分裂将增大树的深度，造成模型过拟合[25]。因此，LightGBM算法在按叶子节点生长过程中会限制树的深度来避免过拟合。

（3）单边梯度采样技术 (减少样本角度)

在梯度提升算法中，每个样本都有不同梯度值，样本的梯度可以反映对模型的贡献程度，通常样本的梯度越大贡献给模型的信息增益越多，而样本的梯度越小，在模型中表现的会越好。

举个例子来说，这里的大梯度样本可以理解为“练习本中的综合性难题”，小梯度样本可以理解为“练习本中的简单题”，对于“简单题”平时做的再多再好，而“难题”却做的很少，在真正的“考试”时还是会表现不好。但并不意味着小梯度样本（“简单题”）就可以直接剔除不用参与训练，因为若直接剔除小梯度样本，数据的分布会发生改变，从而影响模型的预测效果。

因此，LightGBM算法引入了单边梯度采样技术（Gradient-based One-Side Sampling，GOSS），其基本思想就是从减少样本的角度出发，利用样本的梯度大小信息作为样本重要性的考量，保留所有梯度大的样本点（“保留所有难题”），对于梯度小的样本点（“简单题”）按比例进行随机采样，这样既学习了小梯度样本的信息，也学习了大梯度样本的信息（“平时难题都做，简单题做一部分，在面临真正的考试时才可能稳定发挥，甚至超水平发挥”），在不改变原始数据分布的同时，减小了样本数量，提升了模型的训练速度。

（4）互斥特征捆绑（减少特征角度）

高维度的数据通常是非常稀疏的，并且特征之间存在互斥性（例如通过one-hot编码后生成的几个特征不会同时为0），这种数据对模型的效果和运行速度都有一定的影响。

通过互斥特征捆绑算法（Exclusive Feature Bundling，EFB）可以解决高维度数据稀疏性问题，如下图中，设特征1、特征2以及特征3互为互斥的稀疏特征，通过EFB算法，将三个特征捆绑为一个稠密的新特征，然后用这一个新特征替代原来的三个特征，从而实现不损失信息的情况下减少特征维度，避免不必要0值的计算，提升梯度增强算法的速度。

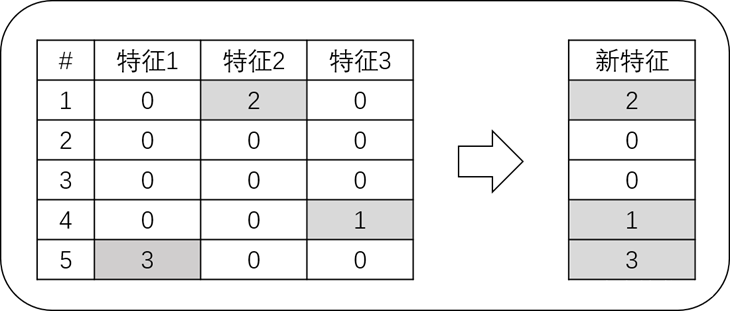
图 EFB特征合并示例

总的来说，LightGBM是一个性能高度优化的GBDT 算法，也可以看成是针对XGBoost的优化算法，可以将LightGBM的优化用公式表达，如下式：LightGBM = XGBoost + Histogram + GOSS + EFB

图 LightGBM算法流程图

4.项目实施步骤

4.1理解数据

首先导入本次实验用到的第三方库并加载数据输出前五行

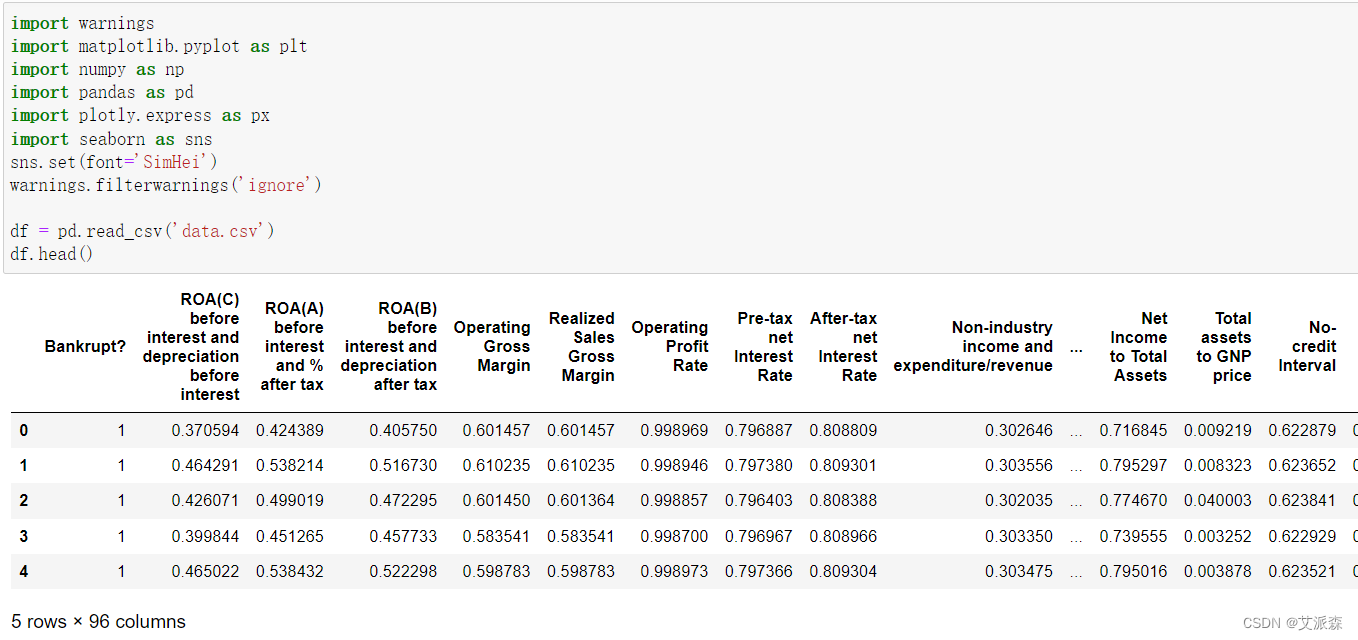
打印数据大小

查看数据基本信息

查看数值型变量的描述性统计

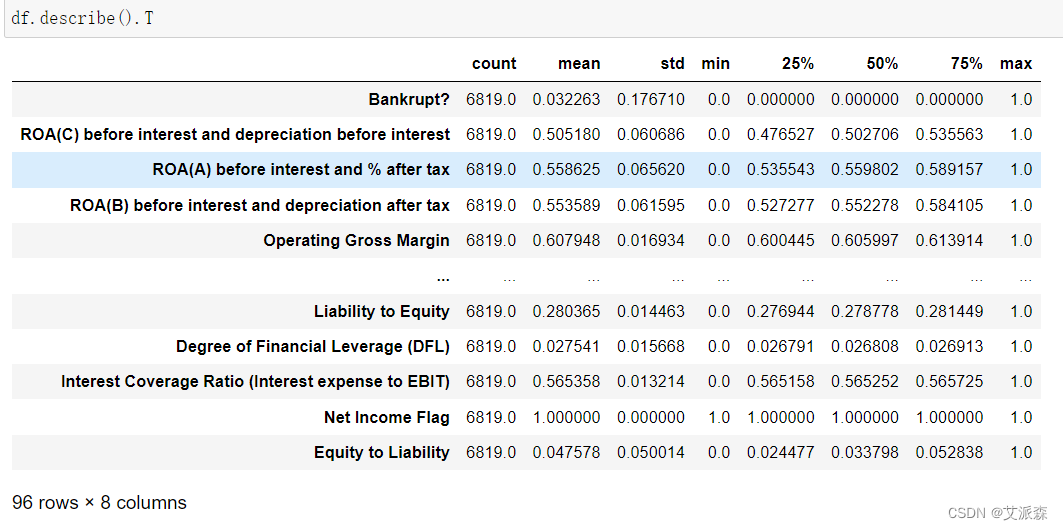
4.2数据预处理

删除缺失值和重复值

4.3探索性数据分析

4.3.1破产比例情况

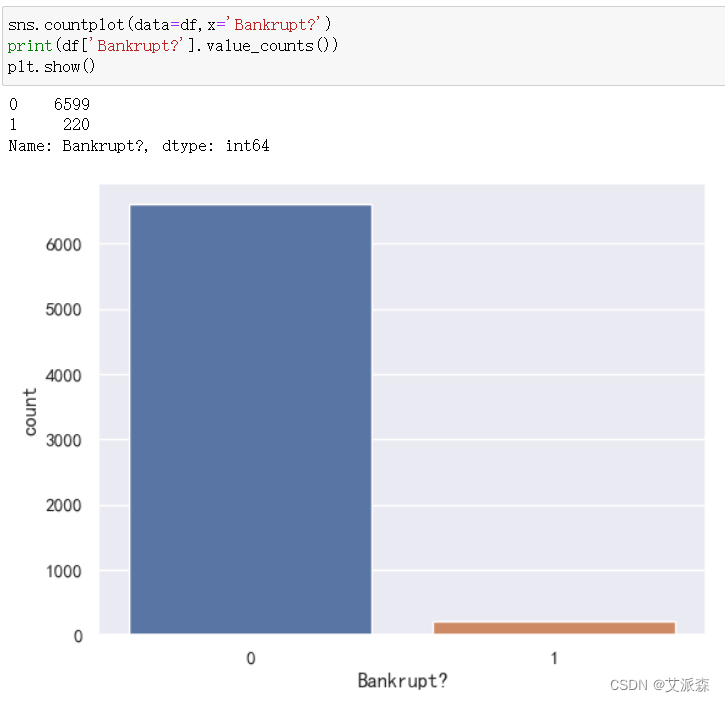
可以看出原始数据集绝大多数都是非破产数据，仅有220条破产公司数据。

4.3.2相关关系可视化

4.3.3正相关可视化

我们可以看到，对于一家破产公司来说，负债率、流动负债与资产以及流动负债与流动资产的数值都很高。

4.3.4负相关可视化

资产和利润越高，公司破产的可能性就越小。

4.4特征工程

准备用于创建公司破产预测模型的数据并对原始数据集进行拆分，其中测试集比例为0.2

4.5模型构建

通过对比五个模型的准确率，我们发现LightGBM模型的准确率最高，故我们最终选择Lightgbm算法模型。

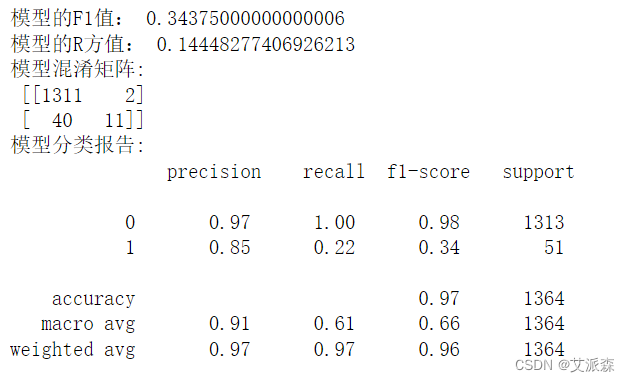
4.6模型评估

对构建的LightGBM算法模型进行评估

4.7特征重要性评分

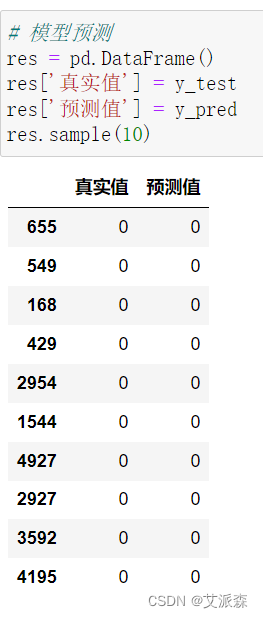
4.8模型预测

随机抽取10个预测结果来检验效果，发现抽取的10个全部预测正确

5.实验总结

本次实验通过分析公司破产数据，我们找出了影响破产的因素，最后我们使用LightGBM算法构建了破产预测模型，模型的准确率为96.9%，模型效果不错。

心得与体会：

通过这次Python项目实战，我学到了许多新的知识，这是一个让我把书本上的理论知识运用于实践中的好机会。原先，学的时候感叹学的资料太难懂，此刻想来，有些其实并不难，关键在于理解。

在这次实战中还锻炼了我其他方面的潜力，提高了我的综合素质。首先，它锻炼了我做项目的潜力，提高了独立思考问题、自我动手操作的潜力，在工作的过程中，复习了以前学习过的知识，并掌握了一些应用知识的技巧等

在此次实战中，我还学会了下面几点工作学习心态：

1）继续学习，不断提升理论涵养。在信息时代，学习是不断地汲取新信息，获得事业进步的动力。作为一名青年学子更就应把学习作为持续工作用心性的重要途径。走上工作岗位后，我会用心响应单位号召，结合工作实际，不断学习理论、业务知识和社会知识，用先进的理论武装头脑，用精良的业务知识提升潜力，以广博的社会知识拓展视野。

2）努力实践，自觉进行主角转化。只有将理论付诸于实践才能实现理论自身的价值，也只有将理论付诸于实践才能使理论得以检验。同样，一个人的价值也是透过实践活动来实现的，也只有透过实践才能锻炼人的品质，彰显人的意志。

3）提高工作用心性和主动性。实习，是开端也是结束。展此刻自我面前的是一片任自我驰骋的沃土，也分明感受到了沉甸甸的职责。在今后的工作和生活中，我将继续学习，深入实践，不断提升自我，努力创造业绩，继续创造更多的价值。

这次Python实战不仅仅使我学到了知识，丰富了经验。也帮忙我缩小了实践和理论的差距。在未来的工作中我会把学到的理论知识和实践经验不断的应用到实际工作中，为实现理想而努力。

源代码

import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import plotly.express as px
import seaborn as sns
sns.set(font='SimHei')
warnings.filterwarnings('ignore')

df = pd.read_csv('data.csv')
df.head()
df.shape
df.info()
df.describe().T
df.dropna(inplace=True)
df.drop_duplicates(inplace=True)
df.shape
sns.countplot(data=df,x='Bankrupt?')
print(df['Bankrupt?'].value_counts())
plt.show()
# 将相关分布与“破产”联系起来
df_corr_bar = df.corr()["Bankrupt?"].sort_values()[:-1]
fig = px.bar(df_corr_bar, orientation="h", color_discrete_sequence=["#34495E "])
fig.update_layout(showlegend=False)
fig.show()
# 得到最正和负的变量'破产?”
numeric_features = df.select_dtypes(include=["float64"]).columns
categorical_features = df.select_dtypes(include=["int64"]).columns

positive_corr = (
    df[numeric_features]
    .corrwith(df["Bankrupt?"])
    .sort_values(ascending=False)[:6]
    .index.tolist()
)
negative_corr = (
    df[numeric_features].corrwith(df["Bankrupt?"]).sort_values()[:6].index.tolist()
)
print(f"{positive_corr}\n\n{negative_corr}")
#　显示正可视化相关
col = 0
row = 0

fig, ax = plt.subplots(2, 3, figsize=(20, 10))

for column in positive_corr:
    sns.barplot(data=df, y=column, x="Bankrupt?", ax=ax[row, col])

    col += 1
    if col > 2:
        row += 1
        col = 0

fig.subplots_adjust(top=0.90)
plt.suptitle("Positive Correlations", fontweight="bold", fontsize=25)
plt.show()
我们可以看到，对于一家破产公司来说，负债率%、流动负债与资产以及流动负债与流动资产的数值都很高。
# 显示负可视化相关
col = 0
row = 0

fig, ax = plt.subplots(2, 3, figsize=(20, 10))

for column in negative_corr:
    sns.barplot(data=df, y=column, x="Bankrupt?", ax=ax[row, col])

    col += 1
    if col > 2:
        row += 1
        col = 0

fig.subplots_adjust(top=0.90)
plt.suptitle("Negatif Correlation", fontweight="bold", fontsize=25)
plt.show()
资产和利润越高，公司破产的可能性就越小
# 准备用于创建公司破产预测模型的数据
from sklearn.model_selection import train_test_split
X = df.drop(["Bankrupt?", " Net Income Flag"], axis=1)
y = df["Bankrupt?"]
# 划分数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=42)
print('训练集大小：',X_train.shape[0])
print('测试集大小：',X_test.shape[0])
# 构建逻辑回归模型
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X_train,y_train)
print('逻辑回归模型准确率：',lr.score(X_test,y_test))
# 构建KNN模型
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(X_train,y_train)
print('KNN模型准确率：',knn.score(X_test,y_test))
# 构建决策树模型
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier()
tree.fit(X_train,y_train)
print('决策树模型准确率：',tree.score(X_test,y_test))
# 构建lightgbm模型
from lightgbm import LGBMClassifier
gbm = LGBMClassifier()
gbm.fit(X_train,y_train)
print('lightgbm模型准确率：',gbm.score(X_test,y_test))
# 构建xgboost模型
from xgboost import XGBClassifier
xgb = XGBClassifier()
xgb.fit(X_train,y_train)
print('xgboost模型准确率：',xgb.score(X_test,y_test))
from sklearn.metrics import f1_score,r2_score,confusion_matrix,classification_report,auc,roc_curve
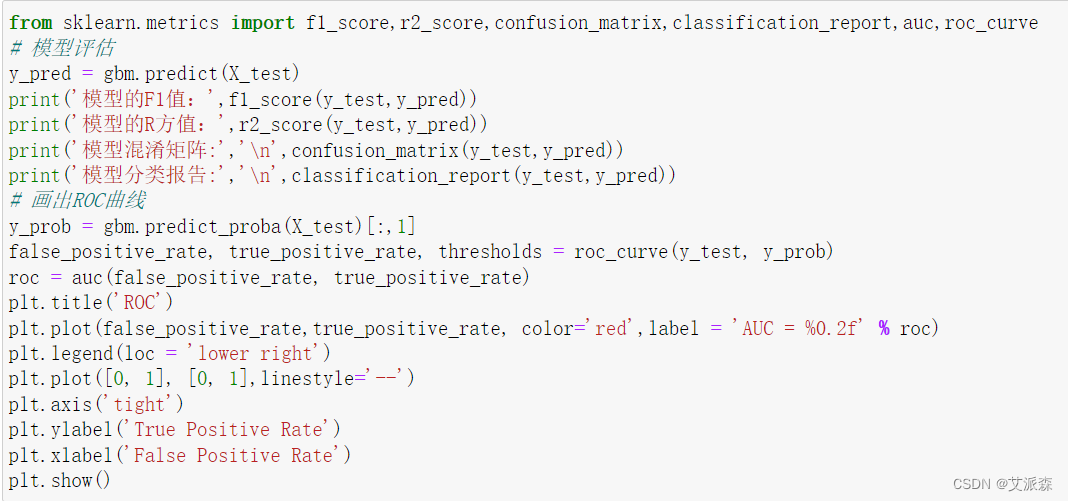
# 模型评估
y_pred = gbm.predict(X_test)
print('模型的F1值：',f1_score(y_test,y_pred))
print('模型的R方值：',r2_score(y_test,y_pred))
print('模型混淆矩阵:','\n',confusion_matrix(y_test,y_pred))
print('模型分类报告:','\n',classification_report(y_test,y_pred))
# 画出ROC曲线
y_prob = gbm.predict_proba(X_test)[:,1]
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_prob) 
roc = auc(false_positive_rate, true_positive_rate)
plt.title('ROC')
plt.plot(false_positive_rate,true_positive_rate, color='red',label = 'AUC = %0.2f' % roc)
plt.legend(loc = 'lower right')
plt.plot([0, 1], [0, 1],linestyle='--')
plt.axis('tight')
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
# 特征重要性评分
feat_labels = X_train.columns[0:]
importances = gbm.feature_importances_
indices = np.argsort(importances)[::-1]
index_list = []
value_list = []
for f,j in zip(range(X_train.shape[1]),indices):
    index_list.append(feat_labels[j])
    value_list.append(importances[j])

plt.figure(figsize=(6,20))
plt.barh(index_list[::-1],value_list[::-1])
plt.yticks(fontsize=12)
plt.title('feature importance',fontsize=14)
plt.show()
# 模型预测
res = pd.DataFrame()
res['真实值'] = y_test
res['预测值'] = y_pred
res.sample(10)