[LeetCode周赛复盘] 第 326 场周赛20230702
- 一、本周周赛总结
- 6909. 最长奇偶子数组
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 6916. 和等于目标值的质数对
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 6911. 不间断子数组
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 6894. 所有子数组中不平衡数字之和
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 参考链接
一、本周周赛总结
- T1 dp。
- T2 两数之和+分解质因数模板。
- T3 有序列表+滑窗。
- T4 维护有序列表+暴力。
6909. 最长奇偶子数组
6909. 最长奇偶子数组
1. 题目描述
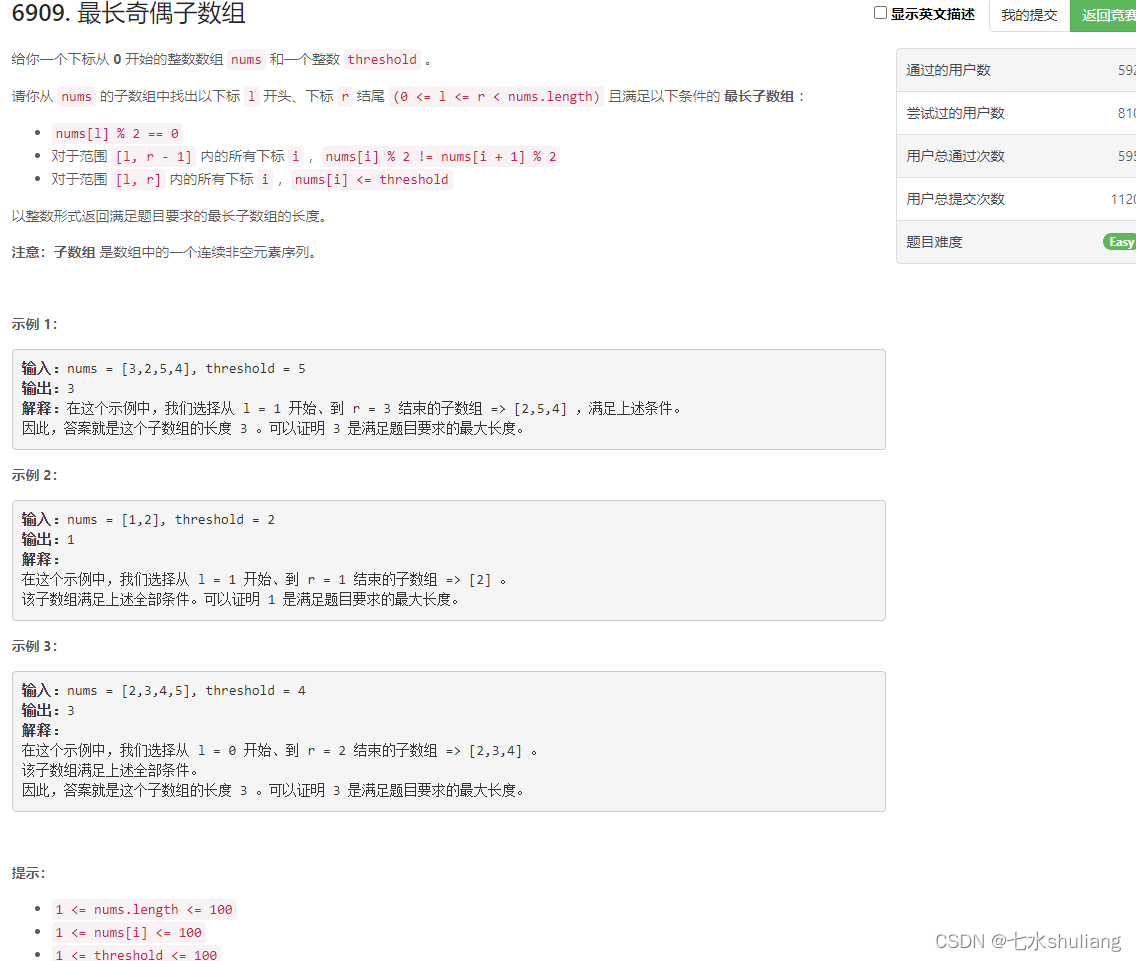
2. 思路分析
- 感觉暴力好麻烦,于是dp了。
- 令f[i]为以i为结尾的最长有效子段。
- 那么可以按照题目要求条件转移。
- 注意:如果nums[i]%2=0,f[i]至少是1。
3. 代码实现
class Solution:
def longestAlternatingSubarray(self, nums: List[int], t: int) -> int:
ans = 0
n = len(nums)
f = [0]*n
if nums[0]%2==0 and nums[0] <= t:
f[0] = 1
for i in range(1,n):
if nums[i] > t:continue
v = nums[i]%2
if v == 0:
f[i] = 1
if v!= nums[i-1]%2 and f[i-1]:
f[i] = 1+f[i-1]
return max(f)
6916. 和等于目标值的质数对
6916. 和等于目标值的质数对
1. 题目描述
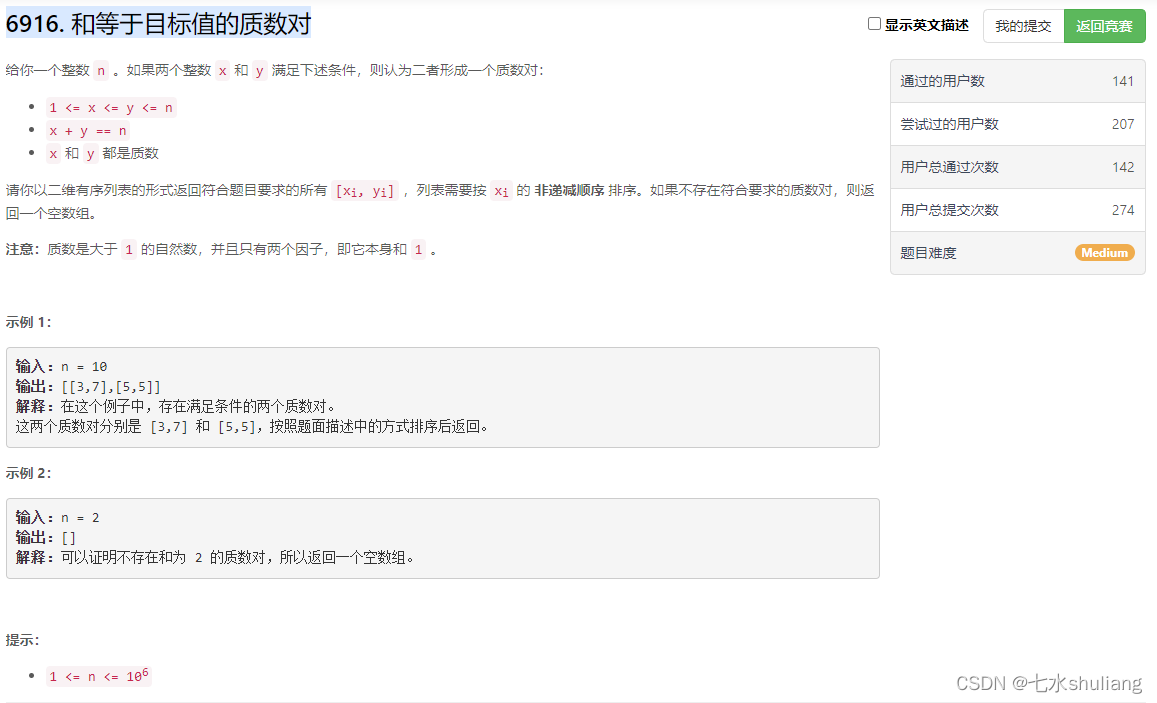
2. 思路分析
贴模板。
- 一看就是两数之和,注意枚举到n//2即可。
3. 代码实现
class PrimeTable:
def __init__(self, n: int) -> None:
self.n = n
self.primes = primes = [] # 所有n以内的质数
self.min_div = min_div = [0] * (n + 1) # md[i]代表i的最小(质)因子
min_div[1] = 1
# 欧拉筛O(n),顺便求出min_div
for i in range(2, n + 1):
if not min_div[i]:
primes.append(i)
min_div[i] = i
for p in primes:
if i * p > n: break
min_div[i * p] = p
if i % p == 0:
break
def is_prime(self, x: int):
"""检测是否是质数,最坏是O(sqrt(x)"""
if x < 3: return x == 2
if x <= self.n: return self.min_div[x] == x
for i in range(2, int(x ** 0.5) + 1):
if x % i == 0: return False
return True
def prime_factorization(self, x: int):
"""分解质因数,复杂度
1. 若x>n则需要从2模拟到sqrt(x),如果中间x降到n以下则走2;最坏情况,不含低于n的因数,则需要开方复杂度
2. 否则x质因数的个数,那么最多就是O(lgx)"""
n, min_div = self.n, self.min_div
for p in range(2, int(x ** 0.5) + 1):
if x <= n: break
if x % p == 0:
cnt = 0
while x % p == 0: cnt += 1; x //= p
yield p, cnt
while 1 < x <= n:
p, cnt = min_div[x], 0
while x % p == 0: cnt += 1; x //= p
yield p, cnt
if x >= n and x > 1:
yield x, 1
def get_factors(self, x: int):
"""求x的所有因数,包括1和x"""
factors = [1]
for p, b in self.prime_factorization(x):
n = len(factors)
for j in range(1, b + 1):
for d in factors[:n]:
factors.append(d * (p ** j))
return factors
def mr_is_prime(self, x):
"""
Miller-Rabin 检测. 检测x是否是质数,置信度: 1 - (1/4)^k. 复杂度k*log^3
但是longlong以内可以用k==3或7的代价,换取100%置信度
https://zhuanlan.zhihu.com/p/349360074
"""
if x < 3 or x % 2 == 0:
return x == 2
if x % 3 == 0:
return x == 3
u, t = x - 1, 0
while not u & 1:
u >>= 1
t += 1
ud = (2, 325, 9375, 28178, 450775, 9780504, 1795265022) # long long 返回用这个7个数检测100%正确
# ud = (2, 7, 61) # int 返回用这3个数检测100%正确
# for _ in range(k):
# a = random.randint(2, x - 2)
for a in ud:
v = pow(a, u, x)
if v == 1 or v == x - 1 or v == 0:
continue
for j in range(1, t + 1):
v = v * v % x
if v == x - 1 and j != t:
v = 1
break
if v == 1:
return False
if v != 1:
return False
return True
pt = PrimeTable(10**6+1)
class Solution:
def findPrimePairs(self, n: int) -> List[List[int]]:
ans = []
for x in pt.primes:
if x > n//2:
break
if pt.is_prime(n-x):
ans.append([x,n-x])
return ans
6911. 不间断子数组
6911. 不间断子数组
1. 题目描述
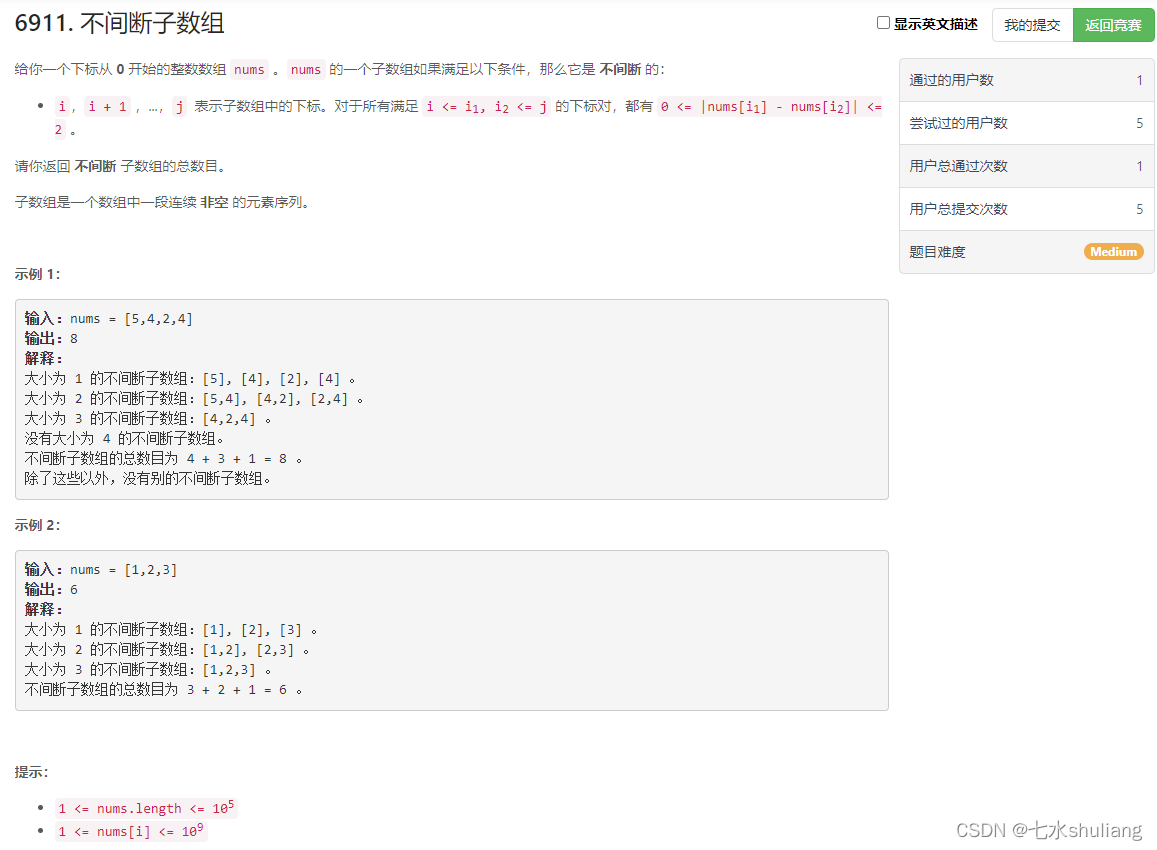
2. 思路分析
- 看起来就是变长滑窗。
- 枚举每个i作为右端点向左能找到的合法窗口,这个窗口内所有数字差应该<=2。
- 那么难点就在于如何维护这个窗口内的最大最小值,直接用有序集合即可。
3. 代码实现
from sortedcontainers import SortedList
class Solution:
def continuousSubarrays(self, nums: List[int]) -> int:
n = len(nums)
q = deque()
s = SortedList()
ans = 0
for v in nums:
q.append(v)
s.add(v)
while s[-1] - s[0]>2:
s.remove(q.popleft())
ans += len(q)
return ans
6894. 所有子数组中不平衡数字之和
6894. 所有子数组中不平衡数字之和
1. 题目描述
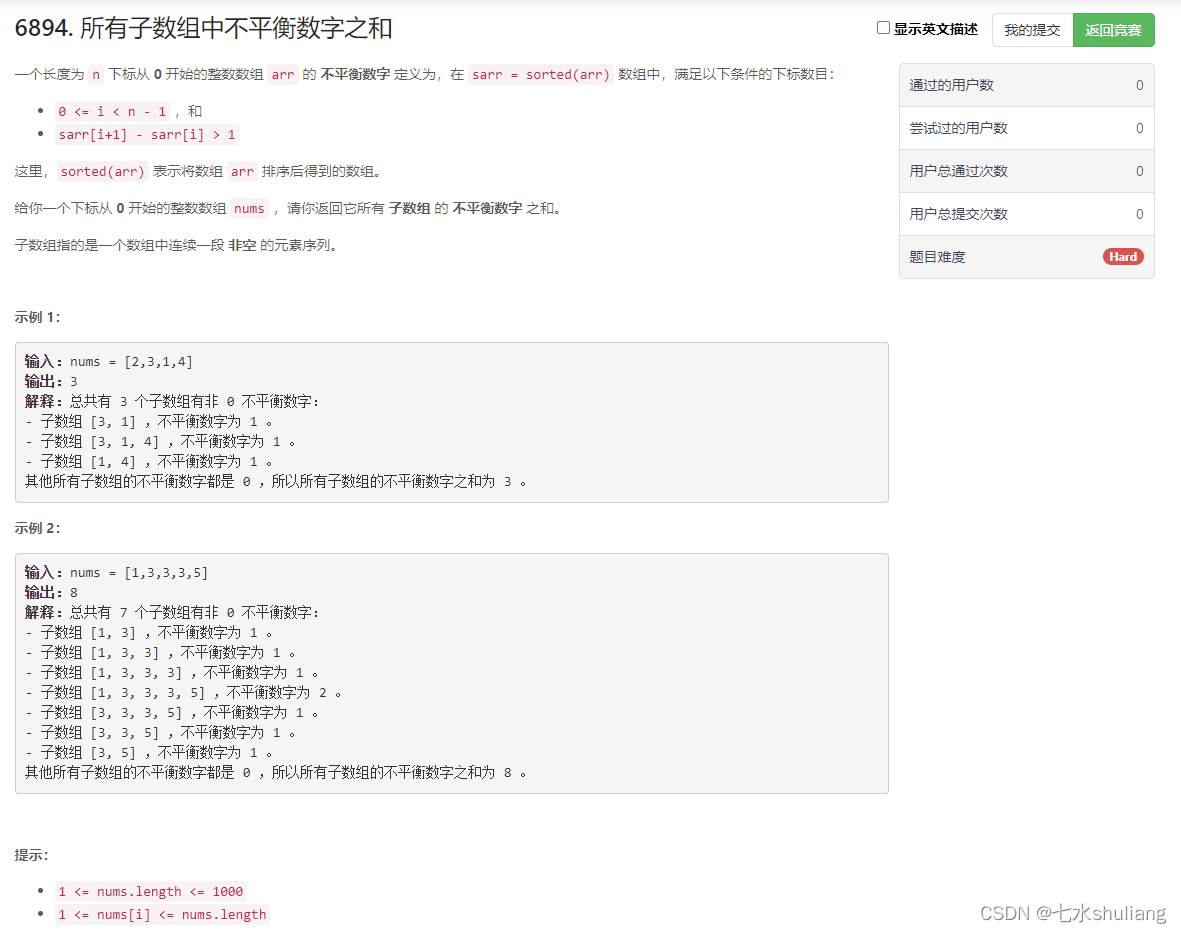
2. 思路分析
- 和昨晚的G差不多。[abc周赛复盘] AtCoder Beginner Contest 308 20230701
- 数据量1000,考虑暴力枚举每个区间。
- 固定左端点,右端点右移时,增加集合内的性质。
- 用有序列表维护集合即可,添加一个数时,会拆分原本相邻的数,减少一个差,增加两个差。
3. 代码实现
from sortedcontainers import SortedList
class Solution:
def sumImbalanceNumbers(self, nums: List[int]) -> int:
n = len(nums)
s = SortedList()
ans = 0
for i in range(n):
s.clear()
p = 0
for j in range(i,n):
v = nums[j]
t = s.bisect_left(v)
if t and t < len(s):
x = s[t] - s[t-1]
if x> 1:
p -= 1
if t:
x = v - s[t-1]
if x > 1:
p += 1
if t < len(s):
x = s[t] - v
if x >1:
p += 1
s.add(v)
ans += p
return ans