算法介绍

摩尔投票法：求众数的方法。

就是维护一个集合，然后我们遍历我们的数组，假如现在我们遍历到的数为x，当集合中都是x的话我们就将x放入集合中，如果我们遍历到的数为x，但是集合中有y，那么我们就会让x带走一个y。到最后我们集合中的主元(y总自己定义的，也就是题目中那个出现次数超过一半的众数) 在集合中的个数一定会为0，并且最后一次也一定是一个会消耗一个x。为啥呢？我们可以采取反证法来证明一下。

宗上所证所以我们可以采取这个1算法求众数。

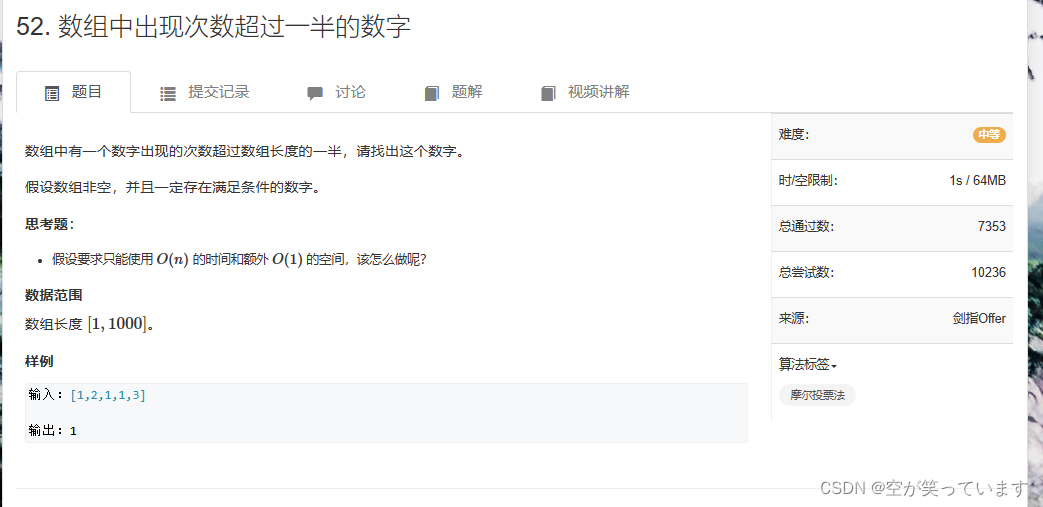
算法题目

ac代码

class Solution {
public:
    int moreThanHalfNum_Solution(vector<int>& nums) {
        int n = nums.size();
        //设主元为x，其个数为cnt。
        int x,cnt=0;
        for(int i=0;i<n;i++){
            if(!cnt) {
                x = nums[i];
                cnt++;
            }
            else if(x==nums[i]&&cnt) cnt++;
            else cnt--;
        }
        return x;
    }
};

这道题虽然代码短，但是很难想出思路，所以理解背下来就行。知道这个算法可以求众数即可。 

算法复杂度

时间复杂度：O(N)

空间复杂度：O(1)

稳定性：稳定。