LeetCode 75 —— 70. 爬楼梯

news2024/9/19 16:55:14

LeetCode 75 —— 70. 爬楼梯

一、题目描述：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1 阶 + 1 阶
2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶

提示：

1 <= n <= 45

来源：力扣（LeetCode）

链接：https://leetcode.cn/problems/climbing-stairs

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

二、思路分析：

这道题考察了什么思想？你的思路是什么？

这道题目我的第一想法自然是递归咯，使用dfs来完成该题，以n为0和1时返回1作为递归退出的出口。至于递归的方法是将n-1和n-2的返回的值之和作为当前 climbStairs(n)的值。
```
func climbStairs(n int) int {
    if n == 0 || n == 1{
        return 1
    }
    return climbStairs(n-1) + climbStairs(n-2)
}
```
但是，万万没有想到，这样居然超时了，当n等于44时，就超时了！

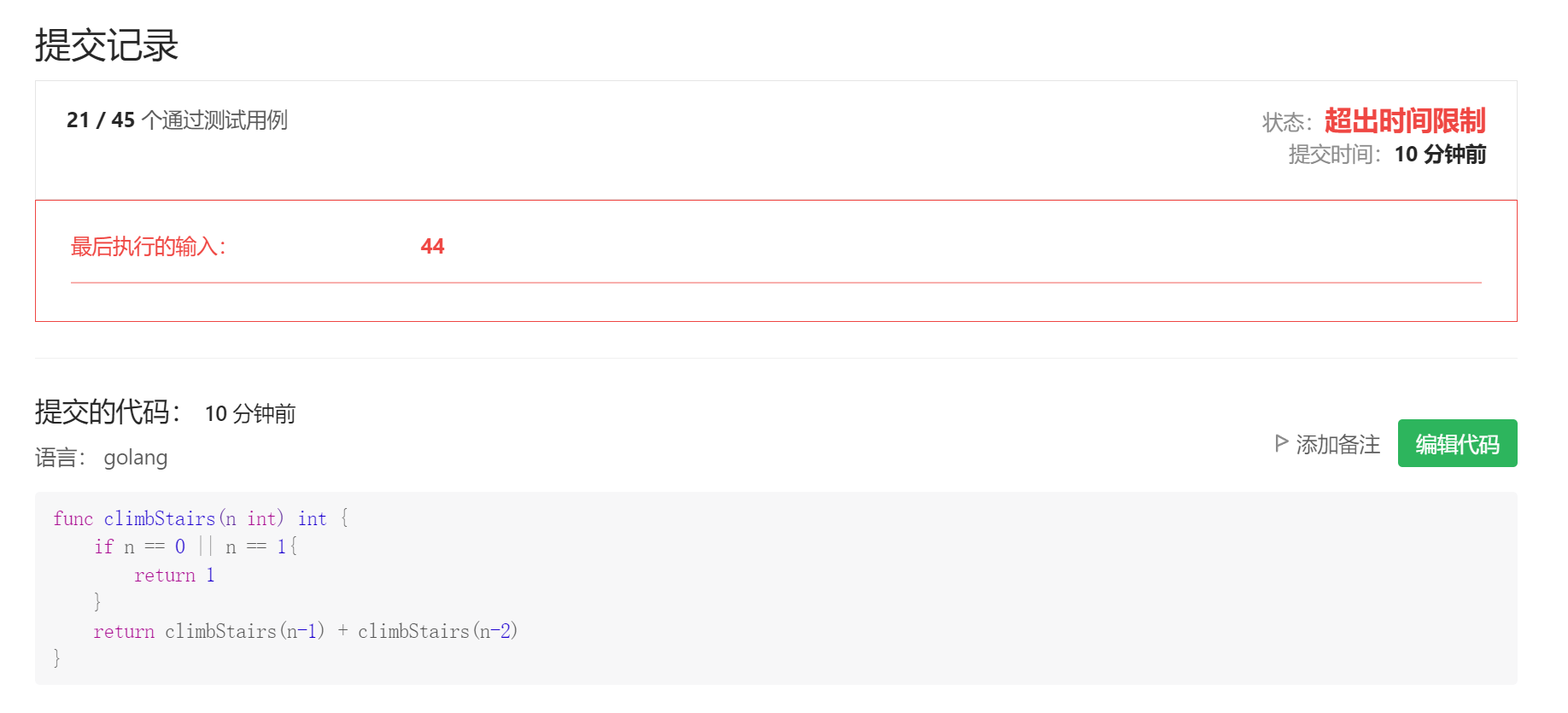
于是，我有一种思路，就是利用切片保存每次计算的结果，每次只需要找到切片元素前面两个值相加即可。我们只需要给切片放入初始值2个1，然后如果n小于2的话，我们就直接返回1。然后从i等于2开始，一直到n，我们将切片元素赋值为前两个元素之和然后放入切片即可。最后返回切片arr的索引为n的元素即可。
```
func climbStairs(n int) int {
   var arr []int = make([]int,0,5)
   if n<2{
       return 1
   }
   arr = append(arr,1,1)
   for i:=2; i<=n; i++{
       arr = append(arr,arr[i-1]+arr[i-2])
   }
   return arr[n]
}
```
做题的时候是不是一次通过的，遇到了什么问题，需要注意什么细节？

不是一次通过的，使用递归的方法会超时，所以我使用数组，以空间换时间，成功解决了此题，不过内存消耗较大！

有几种解法，哪种解法时间复杂度最低，哪种解法空间复杂度最低，最优解法是什么？其他人的题解是什么，谁的效率更好一些？用不同语言实现的话，哪个语言速度最快？

下面这种方法使用的内存就比我的方法少，只需要3个变量即可，不需要保存所有的路径，如果n等于很大的值的话，我那种方法就消耗内存比较多，所以这是一种优化方案！

class Solution {
public:
    int climbStairs(int n) {
        if(n == 1){return 1;}
        if(n == 2){return 2;}
        int a = 1, b = 2, temp;
        for(int i = 3; i <= n; i++){
            temp = a;
            a = b;
            b = temp + b;
        }
        return b;   
    }
};

type matrix [2][2]int

func mul(a, b matrix) (c matrix) {
    for i := 0; i < 2; i++ {
        for j := 0; j < 2; j++ {
            c[i][j] = a[i][0]*b[0][j] + a[i][1]*b[1][j]
        }
    }
    return c
}

func pow(a matrix, n int) matrix {
    res := matrix{{1, 0}, {0, 1}}
    for ; n > 0; n >>= 1 {
        if n&1 == 1 {
            res = mul(res, a)
        }
        a = mul(a, a)
    }
    return res
}

func climbStairs(n int) int {
    res := pow(matrix{{1, 1}, {1, 0}}, n)
    return res[0][0]
}

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/climbing-stairs/solution/pa-lou-ti-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

三、AC 代码：

func climbStairs(n int) int {
   var arr []int = make([]int,0,5)
   if n<2{
       return 1
   }
   arr = append(arr,1,1)
   for i:=2; i<=n; i++{
       arr = append(arr,arr[i-1]+arr[i-2])
   }
   return arr[n]
}