题目链接：力扣

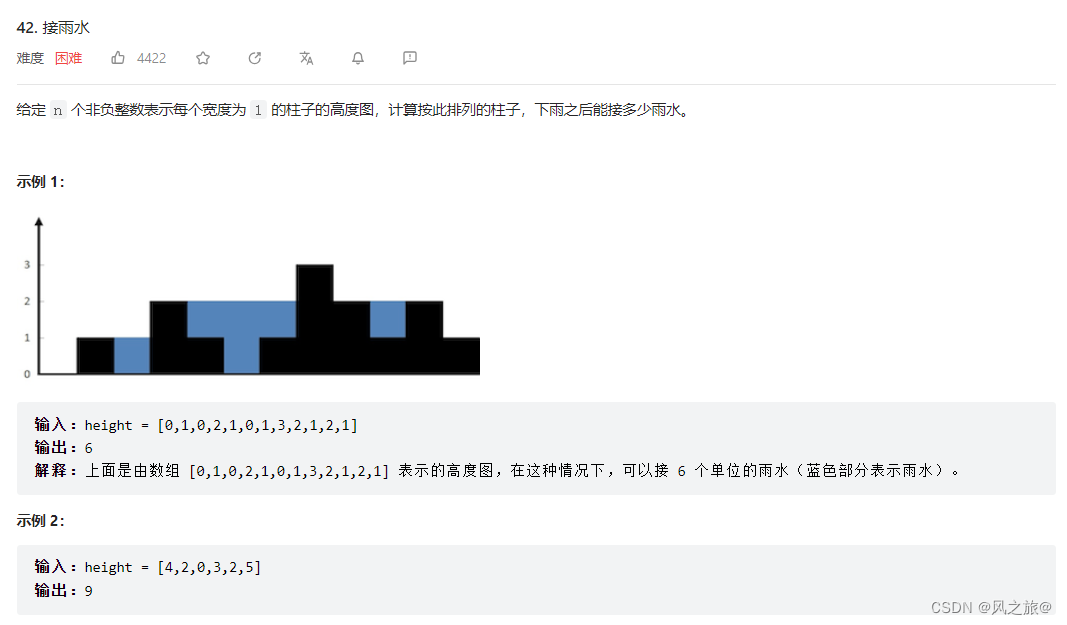
解题思路：从左往右按列进行计算，依次计算每一列能够接到的雨水数量。对于当前列能够接到的雨水数量是由左右两边最高的两根柱子决定的，类似于木桶定律（一只水桶能装多少水取决于它最短的那块木板），即当前列能够接到的雨水数量=Math.min(左边柱子的最大高度，右边柱子的最大高度) - 当前柱子的高度。比如对于第五列来说，左边柱子的最大高度为2，右边柱子的最大高度为3，当前柱子的高度为1，所以第五列能够接到的雨水数量为 2-1=1。

所以如果能够求出当前列柱子的左右两边柱子的最大高度，也就能够计算出所有的雨水数量了。

对于每一列来说，如果使用循环的方式依次向前和向后遍历所有的柱子，求解出最大高度，时间复杂度为O(n^2)，可以使用动态规则求解左右两边柱子的最大高度，时间复杂度为O(n)

创建两个数组：

1. leftMax[]，其中leftMax[i]表示第i列和其左边柱子的最大高度
   1. 初始值，leftMax[0]=height[0]
   2. leftMax[i] = Math.max(leftMax[i-1]，height[i] )
   3. 求解leftMax时从左往右计算
2. rightMax[]，其中rightMax[i]表示第i列和其右边柱子的最大高度
   1. 初始值：rightMax[n-1]=height[n-1]
   2. rightMax[i] = Math.max(rightMax[i+1] , height[i] )
   3. 求解rightMax时从右往左计算

AC代码：

class Solution {
    public static int trap(int[] height) {
        int[] leftMax = new int[height.length];
        int[] rightMax = new int[height.length];
        leftMax[0] = height[0];
        rightMax[height.length - 1] = height[height.length - 1];
        for (int i = 1; i < height.length; i++) {
            leftMax[i]=Math.max(leftMax[i-1],height[i]);
        }
        for (int i = height.length-2;i>=0;i--){
            rightMax[i] = Math.max(rightMax[i+1],height[i]);
        }
        int sum =0;
        for (int i = 0; i < height.length; i++) {
            sum+=Math.min(leftMax[i],rightMax[i])-height[i];
        }
        return sum;
    }
}