数据结构 | 顺序二叉树

news2024/12/24 2:44:48

一、数据结构定义

1、顺序二叉树

/* 顺序二叉树 */
typedef char TreeType;
typedef struct seqTree{
	int MAXNUM;		// 最大元素个数
	int curNum;		// 元素的个数
	TreeType nodelist[];	// 顺序二叉树节点存储
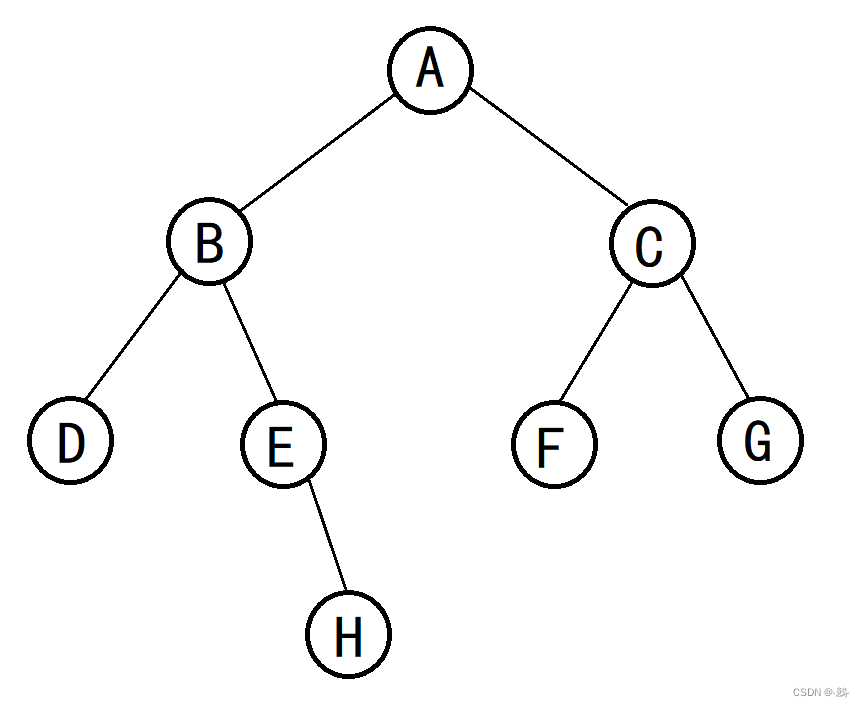
} *SeqTree;

        本次代码中二叉树的结构如下图，用层次序列可以表示为 ABCDEFG###H

 2、链式栈

/* 链式栈 */
typedef char StackType;
typedef struct StackNode {
	StackType data;
	struct StackNode* next;
}StackNode;

typedef struct {
	StackNode* top;
}LinkStack;

二叉树的非递归遍历（先序遍历、中序遍历、后续遍历）需要使用栈进行辅助

二、方法概览

1、二叉树

SeqTree CreateSeqTree(TreeType node[]); // 创建二叉树
int FindTreeNode(SeqTree T, char ch); // 查找指定结点的下标
char GetRoot(SeqTree T); // 求根结点的值
int GetParentIndex(SeqTree T, char ch);		// 求指定结点的双亲结点的下标
int GetLeftChildIndex(SeqTree T, char ch);	// 求指定结点的左孩子的下标
int GetRightChildIndex(SeqTree T, char ch); // 求指定结点的右孩子的下标
void LevelOrder(SeqTree T); // 层序遍历二叉树
void PreOrder(SeqTree T); // 先序遍历二叉树

2、栈

void InitStack(LinkStack* S);//初始化栈
int IsStackEmpty(LinkStack S);//判断栈是否为空
int PushStack(LinkStack* L, StackType data);//入栈
int PopStack(LinkStack* L, StackType* data);//出栈
int GetStackTop(LinkStack* L, StackType* x);//取栈顶元素
int DestroyStack(LinkStack* L);//销毁栈

三、方法详解

1、栈

//初始化栈
void InitStack(LinkStack* S) {
	S->top = (StackNode*)malloc(sizeof(StackNode)); // 分配头节点
	S->top = NULL; //初始化为空
}
//判断栈是否为空
int IsStackEmpty(LinkStack S) {
	if (S.top == NULL) return 1;
	else return 0;
}
//入栈
int PopStack(LinkStack* L, StackType* data) {
	StackNode* del;
	if (L->top == NULL)	return -1;
	else {
		del = L->top;
		*data = del->data;
		L->top = L->top->next;
		free(del);
		return 0;
	}
}
//出栈
int PushStack(LinkStack* L, StackType data) {
	StackNode* news = (StackNode*)malloc(sizeof(struct StackNode));
	if (news == NULL)	return -1;
	else {
		news->data = data;
		news->next = L->top;
		L->top = news;
		return 0;
	}
}
//取栈顶元素
int GetStackTop(LinkStack* L, StackType* x) {
	if (L->top == NULL) {
		*x = NULL;
		return -1;
	}
	else {
		*x = L->top->data;
		return 1;
	}
}
//销毁栈
int DestroyStack(LinkStack* L) {
	int cnt = 0;
	if (L == NULL)	return 0;
	struct StackNode* p = L->top, * q;
	free(L);
	while (p->next != NULL) {
		q = p->next;
		cnt++;
		free(p);
		p = q;
	}
	return cnt;
}

2、二叉树基本操作

// 创建二叉树
SeqTree CreateSeqTree(TreeType node[]) {
	SeqTree T = (SeqTree)malloc(sizeof(struct seqTree));
	for (T->curNum = 0; T->curNum < strlen(node); T->curNum++)
		T->nodelist[T->curNum] = node[T->curNum];
	return T;
}
// 查找指定结点的下标
int FindTreeNode(SeqTree T, char ch) {
	for (int i = 0; i < T->curNum; i++)
		if (T->nodelist[i] == ch)
			return i;
	return -1;
}
// 求根结点的值
char GetRoot(SeqTree T){
	// 若二叉树为空，则返回#
	if (T->curNum == 0) return '#';
	return(T->nodelist[0]);
}
// 求指定结点的双亲结点的下标
int GetParentIndex(SeqTree T, char ch){
	int i, p;
	// 返回双亲结点的下标
	for (i = 0; i < T->curNum; i++) {
		if (T->nodelist[i] == ch) p = i;
	}
	// 若双亲不存在，则返回-1
	if (p <= 0 || p >= T->curNum || T->nodelist[(p - 1) / 2] == 32) return -1;
	return (p - 1) / 2;
}
// 求指定结点的左孩子的下标
int GetLeftChildIndex(SeqTree T, char ch){
	int i, p;
	for (i = 0; i < T->curNum; i++) {
		if (T->nodelist[i] == ch) p = i;
	}
	// 若左孩子不存在，则返回-1
	if (p < 0 || p >= T->curNum || T->nodelist[2 * p + 1] == 32)
		return -1;
	return 2 * p + 1;
}
// 求指定结点的右孩子的下标
int GetRightChildIndex(SeqTree T, char ch){
	int i, p;
	for (i = 0; i < T->curNum; i++) {
		if (T->nodelist[i] == ch) p = i;
	}
	// 若左孩子不存在，则返回-1
	if (p < 0 || p >= T->curNum || T->nodelist[2 * (p + 1)] == 32) 
		return -1;
	return 2 * (p + 1);
}

3、二叉树递归遍历

（1）层次遍历

// 层序遍历二叉树
void LevelOrder(SeqTree T){
	for (int i = 0; i < T->curNum; i++) {
		if (T->nodelist[i] == '#');
		else printf("%c ", T->nodelist[i]);
	}
}

（2）先序遍历

// 先序遍历二叉树
void PreOrder(SeqTree T){
	char c;
	LinkStack s;
	InitStack(&s);
	PushStack(&s, T->nodelist[0]);

	while (!IsStackEmpty(s)) {
		GetStackTop(&s, &c);
		PopStack(&s, &c);
		if (FindTreeNode(T, c) != -1) {
			if (c == '#');
			else printf("%c ", c);
			PushStack(&s, T->nodelist[GetRightChildIndex(T, c)]);
			PushStack(&s, T->nodelist[GetLeftChildIndex(T, c)]);
		}
	}
}

四、运行结果

        main方法代码如下：

int main(void) {
	TreeType node[15] = { 'A','B','C','D','E','F','G','#','#','#','H'};
	SeqTree T = CreateSeqTree(node);

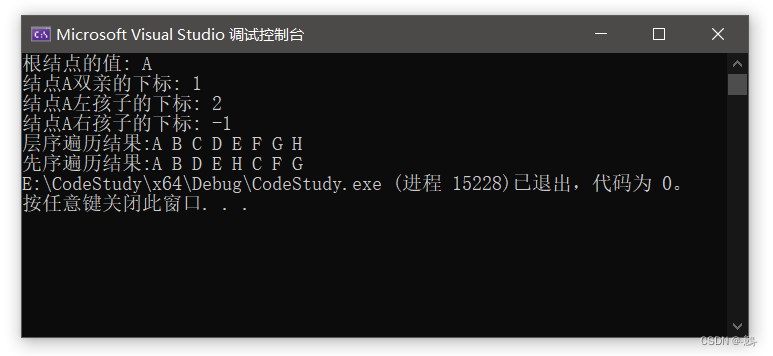
	printf("根结点的值: %c", GetRoot(T));
	printf("\n结点A双亲的下标: %d", GetLeftChildIndex(T, 'A'));
	printf("\n结点A左孩子的下标: %d", GetRightChildIndex(T, 'A'));
	printf("\n结点A右孩子的下标: %d", GetParentIndex(T, 'A'));

	printf("\n层序遍历结果:");
	LevelOrder(T);
	printf("\n先序遍历结果:");
	PreOrder(T);
}

        运行结果如下：

 

 五、源代码

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>


/* 顺序二叉树 */
typedef char TreeType;
typedef struct seqTree{
	int MAXNUM;		// 最大元素个数
	int curNum;		// 元素的个数
	TreeType nodelist[];	// 顺序二叉树节点存储
} *SeqTree;

/* 链式栈 */
typedef char StackType;
typedef struct StackNode {
	StackType data;
	struct StackNode* next;
}StackNode;

typedef struct {
	StackNode* top;
}LinkStack;

void InitStack(LinkStack* S);//初始化栈
int IsStackEmpty(LinkStack S);//判断栈是否为空
int PushStack(LinkStack* L, StackType data);//入栈
int PopStack(LinkStack* L, StackType* data);//出栈
int GetStackTop(LinkStack* L, StackType* x);//取栈顶元素
int DestroyStack(LinkStack* L);//销毁栈

SeqTree CreateSeqTree(TreeType node[]); // 创建二叉树
int FindTreeNode(SeqTree T, char ch); // 查找指定结点的下标
char GetRoot(SeqTree T); // 求根结点的值
int GetParentIndex(SeqTree T, char ch);		// 求指定结点的双亲结点的下标
int GetLeftChildIndex(SeqTree T, char ch);	// 求指定结点的左孩子的下标
int GetRightChildIndex(SeqTree T, char ch); // 求指定结点的右孩子的下标
void LevelOrder(SeqTree T); // 层序遍历二叉树
void PreOrder(SeqTree T); // 先序遍历二叉树

/*------------- 栈基本操作 ---------------*/
//初始化栈
void InitStack(LinkStack* S) {
	S->top = (StackNode*)malloc(sizeof(StackNode)); // 分配头节点
	S->top = NULL; //初始化为空
}
//判断栈是否为空
int IsStackEmpty(LinkStack S) {
	if (S.top == NULL) return 1;
	else return 0;
}
//入栈
int PopStack(LinkStack* L, StackType* data) {
	StackNode* del;
	if (L->top == NULL)	return -1;
	else {
		del = L->top;
		*data = del->data;
		L->top = L->top->next;
		free(del);
		return 0;
	}
}
//出栈
int PushStack(LinkStack* L, StackType data) {
	StackNode* news = (StackNode*)malloc(sizeof(struct StackNode));
	if (news == NULL)	return -1;
	else {
		news->data = data;
		news->next = L->top;
		L->top = news;
		return 0;
	}
}
//取栈顶元素
int GetStackTop(LinkStack* L, StackType* x) {
	if (L->top == NULL) {
		*x = NULL;
		return -1;
	}
	else {
		*x = L->top->data;
		return 1;
	}
}
//销毁栈
int DestroyStack(LinkStack* L) {
	int cnt = 0;
	if (L == NULL)	return 0;
	struct StackNode* p = L->top, * q;
	free(L);
	while (p->next != NULL) {
		q = p->next;
		cnt++;
		free(p);
		p = q;
	}
	return cnt;
}

/*------------- 树基本操作 ---------------*/
// 创建二叉树
SeqTree CreateSeqTree(TreeType node[]) {
	SeqTree T = (SeqTree)malloc(sizeof(struct seqTree));
	for (T->curNum = 0; T->curNum < strlen(node); T->curNum++)
		T->nodelist[T->curNum] = node[T->curNum];
	return T;
}
// 查找指定结点的下标
int FindTreeNode(SeqTree T, char ch) {
	for (int i = 0; i < T->curNum; i++)
		if (T->nodelist[i] == ch)
			return i;
	return -1;
}
// 求根结点的值
char GetRoot(SeqTree T){
	// 若二叉树为空，则返回#
	if (T->curNum == 0) return '#';
	return(T->nodelist[0]);
}
// 求指定结点的双亲结点的下标
int GetParentIndex(SeqTree T, char ch){
	int i, p;
	// 返回双亲结点的下标
	for (i = 0; i < T->curNum; i++) {
		if (T->nodelist[i] == ch) p = i;
	}
	// 若双亲不存在，则返回-1
	if (p <= 0 || p >= T->curNum || T->nodelist[(p - 1) / 2] == 32) return -1;
	return (p - 1) / 2;
}
// 求指定结点的左孩子的下标
int GetLeftChildIndex(SeqTree T, char ch){
	int i, p;
	for (i = 0; i < T->curNum; i++) {
		if (T->nodelist[i] == ch) p = i;
	}
	// 若左孩子不存在，则返回-1
	if (p < 0 || p >= T->curNum || T->nodelist[2 * p + 1] == 32)
		return -1;
	return 2 * p + 1;
}
// 求指定结点的右孩子的下标
int GetRightChildIndex(SeqTree T, char ch){
	int i, p;
	for (i = 0; i < T->curNum; i++) {
		if (T->nodelist[i] == ch) p = i;
	}
	// 若左孩子不存在，则返回-1
	if (p < 0 || p >= T->curNum || T->nodelist[2 * (p + 1)] == 32) 
		return -1;
	return 2 * (p + 1);
}

// 层序遍历二叉树
void LevelOrder(SeqTree T){
	for (int i = 0; i < T->curNum; i++) {
		if (T->nodelist[i] == '#');
		else printf("%c ", T->nodelist[i]);
	}
}
// 先序遍历二叉树
void PreOrder(SeqTree T){
	char c;
	LinkStack s;
	InitStack(&s);
	PushStack(&s, T->nodelist[0]);

	while (!IsStackEmpty(s)) {
		GetStackTop(&s, &c);
		PopStack(&s, &c);
		if (FindTreeNode(T, c) != -1) {
			if (c == '#');
			else printf("%c ", c);
			PushStack(&s, T->nodelist[GetRightChildIndex(T, c)]);
			PushStack(&s, T->nodelist[GetLeftChildIndex(T, c)]);
		}
	}
}


int main(void) {
	TreeType node[15] = { 'A','B','C','D','E','F','G','#','#','#','H'};
	SeqTree T = CreateSeqTree(node);

	printf("根结点的值: %c", GetRoot(T));
	printf("\n结点A双亲的下标: %d", GetLeftChildIndex(T, 'A'));
	printf("\n结点A左孩子的下标: %d", GetRightChildIndex(T, 'A'));
	printf("\n结点A右孩子的下标: %d", GetParentIndex(T, 'A'));

	printf("\n层序遍历结果:");
	LevelOrder(T);
	printf("\n先序遍历结果:");
	PreOrder(T);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/708699.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Python】字典

【Python】字典

文章目录 一. 字典的创建二. 字典的操作1. 查找 key2. 新增键值对3. 删除键值对4. 遍历字典4.1 使用 for 循环遍历字典4.2 通过方法遍历字典keys() 获取到字典中所有 keyvalues() 获取到字典中的所以 valueitems 获取到字典中的所有键值对 三. 理解字典操作的效率 一. 字典的创…
阅读更多...
Linux--打印文件内容：cat

Linux--打印文件内容：cat

cat是cater的简写 语法&#xff1a; cat [选项] [文件] 常用选项&#xff1a; -b 对非空输出行编号 -n 对输出的所有行编号 -s 不输出多行空行 示例&#xff1a; ①打印文件hello.c的内容 ②带行号打印文件hello.c的内容 ③输入什么&#xff0c;打印什么 ④输入重定向&…
阅读更多...
讲座笔记：如何撰写高质量科技论文

讲座笔记：如何撰写高质量科技论文

1 论文总体思路 2 摘要 3 Intro 常见Introduction逻辑&#xff1a; 说明问题是什么&#xff1b;简单罗列前人工作&#xff1b;描述我们的工作。 说明问题是什么&#xff1b;目前最好的工作面临什么挑战&#xff1b;我们的方法能缓解上述挑战 3.1 段落写法 首先列出几句话 …
阅读更多...
【 Linux】文件删除原理

【 Linux】文件删除原理

文章目录 Linux文件删除原理文件的索引节点和链接文件删除的过程文件删除后是否能恢复 Linux文件删除原理 Linux是一个强大的操作系统&#xff0c;它提供了许多命令和工具来管理文件和目录。其中&#xff0c;最常用的命令之一就是rm&#xff0c;它可以用来删除不需要的文件或目…
阅读更多...
Less简明教程

Less简明教程

一.概述 Less是一种动态样式语言&#xff0c;它在CSS的基础上扩展了混合、嵌套、变量等实用功能。Less也是一种CSS预处理语言&#xff0c;less文件在经过less.js处理后&#xff0c;最终会生成.css文件&#xff0c;如下图所示&#xff1a; 1.动态样式语言的比较 动态样式语言主…
阅读更多...
git push报错rejected：no-fast-forward

git push报错rejected：no-fast-forward

报错&#xff1a; 报错关键词&#xff1a; non-fast-forwardyour current branch is behindthe remote changes 即&#xff1a;不能快速前进、当前分支滞后、远端改变 原因&#xff1a; 这个分支下&#xff0c;别人提交了一些代码到远程仓库。对于这个改变&#xff0c;你没有…
阅读更多...
SpringBoot+微信小程序在线订餐小程序系统 附带详细运行指导视频

SpringBoot+微信小程序在线订餐小程序系统 附带详细运行指导视频

文章目录 一、项目演示二、项目介绍三、运行截图四、主要代码 一、项目演示 项目演示地址&#xff1a; 视频地址 二、项目介绍 项目描述&#xff1a;这是一个基于SpringBoot微信小程序框架开发的在线订餐小程序系统。首先&#xff0c;这是一个前后端分离的项目&#xff0c;代…
阅读更多...
什么是 Kubernetes 服务器端应用 (SSA)？

什么是 Kubernetes 服务器端应用 (SSA)？

自 2021 年 8 月 v1.22 版本发布以来，服务器端应用 (SSA) 已在 Kubernetes 中普遍可用。这是一种声明式资源管理策略，可通过将命令逻辑移至kubectl apply服务器来改进 diff 计算并警告合并冲突。 本文将解释 SSA 的工作原理以及为什么它比以前的客户端应用 (CSA) 方法更受青…
阅读更多...
Python3 面向对象 | 菜鸟教程（十六）

Python3 面向对象 | 菜鸟教程（十六）

目录 一、面向对象技术简介 &#xff08;一&#xff09;类(Class) &#xff08;二&#xff09;方法 &#xff08;三&#xff09;类变量 &#xff08;四&#xff09;数据成员 &#xff08;五&#xff09;方法重写 &#xff08;六&#xff09;局部变量 &#xff08;七&am…
阅读更多...
并发-抽象队列同步器AQS应用Lock详解

并发-抽象队列同步器AQS应用Lock详解

锁的膨胀是指synchronized原本是无锁态&#xff0c;当有一个线程调用时变为偏向锁&#xff0c;当有多个线程排队自旋等待锁时会升级为轻量锁&#xff0c;当线程等待时间太长时会升级为重量级锁&#xff0c;这就是锁的膨胀过程&#xff0c;且是不可逆的。 锁的粗化是指如果在一个…
阅读更多...
【总结】1727- 前端开发中如何高效地模拟数据？

【总结】1727- 前端开发中如何高效地模拟数据？

&#x1f449; 「文章推荐」 详细聊一聊 Vue3 动态组件深入浅出 Vue3 自定义指令6 个你必须明白 Vue3 的 ref 和 reactive 问题初中级前端必须掌握的 10 个 Vue 优化技巧分享 15 个 Vue3 全家桶开发的避坑经验 在开发和测试工作中&#xff0c;mock 数据非常实用。mock 数据是指…
阅读更多...
基于值的深度强化学习算法

基于值的深度强化学习算法

目录 DQN2013 —— Playing Atari with Deep Reinforcement LearningDQN2015 —— Human-level control through deep reinforcement learning引用文献 DQN2013 —— Playing Atari with Deep Reinforcement Learning 论文下载地址 论文介绍 该论文提出了一个基于卷积神经网络…
阅读更多...
数字IC验证环境的创建

数字IC验证环境的创建

本文介绍了从一组可重用的验证组件中构建测试平台所需的步骤。UVM促进了重用&#xff0c;加速了测试平台构建的过程。 首先对测试平台集成者&#xff08;testbench integrator&#xff09;和测试编写者&#xff08;test writer &#xff09;进行区分&#xff0c;前者负责测试平…
阅读更多...
【Java EE】-博客系统二(前后端分离)

【Java EE】-博客系统二(前后端分离)

作者&#xff1a;学Java的冬瓜 博客主页&#xff1a;☀冬瓜的主页&#x1f319; 专栏&#xff1a;【JavaEE】 分享: 徘徊着的 在路上的 你要走吗 易碎的 骄傲着 那也曾是我的模样 ——《平凡之路》 主要内容&#xff1a;显示用户信息、上传头像、新增博客、删除博客、修改博客…
阅读更多...
Android:设计模式

Android:设计模式

文章参考来源1 文章参考来源2 文章参考来源3 MVC Model 数据来源&#xff0c;管理业务数据逻辑&#xff0c;读取数据等 View 视图 Controller 单例模式&#xff0c;处理业务逻辑&#xff0c;负责改变Model和View 经典的MVC架构是 用户点击View&#xff0c;View将用户输入转…
阅读更多...
springboot详细整合mybatisplus

springboot详细整合mybatisplus

SpringBoot详细整合mybatisPlus 文章目录 SpringBoot详细整合mybatisPlus一、引入mybatis_plus依赖二、修改mybatis_plus的yml配置三、添加mybatis_plus的其他配置以及包扫描四&#xff0c;修改mybatis的配置&#xff08;这一步根据实际情况修改&#xff09; 无奈&#xff0c;一…
阅读更多...
三个关键数字变化，剖析中国智能手机市场的趋势及其影响

三个关键数字变化，剖析中国智能手机市场的趋势及其影响

近期&#xff0c;全球行业分析机构CounterpointResearch公布了《中国智能手机高端市场白皮书》&#xff0c;对中国智能手机市场数据进行详细分析。该报告揭示了几个关键数据&#xff0c;值得深入剖析。 上面的图表展示了中国智能手机市场在2012年至2022年的11年间销量、平均价格…
阅读更多...
UE5《Electric Dreams》项目PCG技术解析 之 PCGDemo_Ditch关卡详解

UE5《Electric Dreams》项目PCG技术解析 之 PCGDemo_Ditch关卡详解

文章目录 前导文章关卡概要PCGGraphPoints From Actor Tag作为PCG的分割工具分层装饰 一些知识点和技巧使用Attribute Operation将属性暂存到临时属性中是否生成碰撞 小结 前导文章 《UE5《Electric Dreams》项目PCG技术解析 之 基于关卡PCGSettings的工作流》《UE5《Electric…
阅读更多...
mac系统通过终端连接远程服务器

mac系统通过终端连接远程服务器

mac系统通过终端连接远程服务器 1、通过自带终端连接1.1 命令直接连接1.2 方式2——创建连接 2、通过iTerm2连接2.1 方式一&#xff1a;命令直接连接 3. Mac上使用scp命令 1、通过自带终端连接 1.1 命令直接连接 如下&#xff1a;ssh -p 22 root远程IP1.2 方式2——创建连接 …
阅读更多...
类Twitter风格的RSS阅读器

类Twitter风格的RSS阅读器

本文完成于 2 月中旬&#xff0c;其中的反代还是 frp npm 方案&#xff1b; 什么是 RSS ? RSS 是用 PHP、Laravel、Inertia.js、Tailwind 和 Vue.js 编写的简单的类Twitter 风格的 RSS阅读器&#xff0c;支持 RSS和ATOM 格式。 命令行安装 在群晖上以 Docker 方式安装。 官…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023