文章目录
- 前言
- 课前温习
- 一、单链表
- 核心模板
- 1.1题目描述
- 1.2思路分析
- 1.3代码实现
- 二、双链表
- 核心模板
- 2.1题目描述
- 2.2思路分析
- 2.3代码实现
- 三、栈
- 核心模板
- 3.1题目描述
- 3.2思路分析
- 3.3代码实现
- 四、队列
- 核心模板
- 4.1题目描述
- 4.2思路分析
- 4.3代码实现
- 五、单调栈
- 核心模板
- 5.1题目描述
- 5.2思路分析
- 5.3代码实现
- 六、单调队列
- 核心模板
- 6.1题目描述
- 6.2思路分析
- 6.3代码实现
- 七、KMP算法
- 核心模板
- 7.1题目描述
- 7.2思路分析
- 7.3代码实现
- 八、Trie树
- 核心模板
- 8.1题目描述
- 8.2思路分析
- 8.3代码实现
- 九、并查集
- 核心模板
- 题目一
- 9.1题目描述
- 9.2思路分析
- 9.3代码实现
- 题目二
- 9.1题目描述
- 9.2思路分析
- 9.3代码实现
- 十、堆
- 核心模板
- 题目一
- 10.1题目描述
- 10.2思路分析
- 10.3代码实现
- 题目二
- 10.1题目描述
- 10.2思路分析
- 10.3代码实现
- 十一、一般哈希
- 核心模板
- 11.1题目描述
- 11.2思路分析
- 11.3代码实现
- 十二、字符串哈希
- 核心模板
- 12.1题目描述
- 12.2思路分析
- 12.3代码实现
- 十三、STL简介
前言
本专栏文章为本人AcWing算法基础课的学习笔记,课程地址在这。如有侵权,立即删除。
课前温习

一、单链表
邻接表:存储图和树
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-o4Pk9X1T-1687962983149)(https://note.youdao.com/yws/res/2277/WEBRESOURCE8c789d299ebf0ba45d237919c6798d16)]](https://img-blog.csdnimg.cn/a95efdacd62a48f1a7b341e5f85f82c4.png)
e数组存储每个结点的值,ne数组存储每个结点的指向的下一个结点。
- 数组模拟链表比较快,指针模拟会涉及到new操作,比较慢。
核心模板
//head存储链表头,e数组存储结点值,ne数组存储结点的next指针,idx表示当前用到了哪个结点
int head,e[N],ne[N],idx;
//初始化
void init(){
head=-1;
idx=0;
}
//在链表头插入一个数a
void insert(int a){
e[idx]=a,ne[idx]=head,head=idx++;
}
//将头结点删除,需要保证头结点存在
void remove(){
head=ne[head];
}
题目链接:826. 单链表
1.1题目描述
实现一个单链表,链表初始为空,支持三种操作:
向链表头插入一个数;
删除第 k 个插入的数后面的数;
在第 k 个插入的数后插入一个数。
现在要对该链表进行 M 次操作,进行完所有操作后,从头到尾输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数,则按照插入的时间顺序,这 n 个数依次为:第 1 个插入的数,第 2 个插入的数,…第 n 个插入的数。输入格式
第一行包含整数 M,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令可能为以下几种:
H x,表示向链表头插入一个数 x。
D k,表示删除第 k 个插入的数后面的数(当 k 为 0 时,表示删除头结点)。
I k x,表示在第 k 个插入的数后面插入一个数 x(此操作中 k 均大于 0)。输出格式
共一行,将整个链表从头到尾输出。
数据范围
1≤M≤100000
所有操作保证合法。输入样例:
10 H 9 I 1 1 D 1 D 0 H 6 I 3 6 I 4 5 I 4 5 I 3 4 D 6输出样例:
6 4 6 5
1.2思路分析
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aGtPCV18-1687962983150)(https://note.youdao.com/yws/res/2602/WEBRESOURCE45efbc38998caa20a2d6f3d9eccba0a6)]](https://img-blog.csdnimg.cn/eba1581708e04f67bdb3aece502955ca.png)
插入操作:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1rNzBeTe-1687962983151)(https://note.youdao.com/yws/res/2604/WEBRESOURCEf54de51e46605e55a3760e3a260484bc)]](https://img-blog.csdnimg.cn/8b147c2a6e1c43df957a2529b07a883e.png)
删除操作:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PUwJM2Gg-1687962983152)(https://note.youdao.com/yws/res/2609/WEBRESOURCE7fbbdc13b47df9bcdbcad4d2ce473e0e)]](https://img-blog.csdnimg.cn/c7fa460752984f138416e81c946e4165.png)
1.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
//head表示头结点的下标
//e[i]表示结点i的值
//ne[i]表示结点的next的指针(i的下一个点的下标)
//idx表示当前用到了哪个点(点的编号/下标)
int head,e[N],ne[N],idx;
//初始化
void init(){
head=-1;
idx=0;
}
//将x插到头结点
void add_to_head(int x){
e[idx]=x; //保存当前结点的值
ne[idx]=head; //将新结点的next指针指向head
head=idx; //将新结点更新为头结点
idx++;
}
//将x插到下标为k的点的后面
void add(int k,int x){
e[idx]=x; //保存当前结点的值
ne[idx]=ne[k]; //将新结点的next指针指向下标为k的点的下一位结点
ne[k]=idx; //将下标为k的结点的next指针指向新结点
idx++;
}
//将下标为k的点的后面的点删掉
void remove(int k){
ne[k]=ne[ne[k]]; //将下标为k的结点的next指针指向下标为k的结点的下一位的下一位结点
}
int main(){
int m;
cin>>m;
init();
while(m--){
int k,x;
char op;
cin>>op;
if(op=='H'){
cin>>x;
add_to_head(x);
}
else if(op=='D'){
cin>>k;
if(!k) head=ne[head]; //如果删除的数是头结点,下标为0,需要先将头结点更新为头结点的下一位,否则将无法访问链表元素,造成内存泄漏
remove(k-1); //此处k代表第k个数,第k个数下标为k-1,下同
}
else{
cin>>k>>x;
add(k-1,x);
}
}
for(int i=head;i!=-1;i=ne[i]){
cout<<e[i]<<" ";
}
return 0;
}
二、双链表
用于优化某些问题
核心模板
//e数组存储结点的值,l数组存储结点的左指针,r数组存储结点右指针,idx表示当前用到了哪个结点
int e[N],l[N],r[N],idx;
//初始化
void init(){
//0是左端点,1是右端点
r[0]=1,l[1]=0; //0号点的右边是1号点,1号点的左边是0号点
idx=2;
}
//在结点a的右边插入一个数x
void insert(int a,int x){
e[idx]=x;
l[idx]=a,r[idx]=r[a];
l[r[a]]=idx,r[a]=idx++;
}
//删除结点a
void remove(int a){
l[r[a]]=l[a];
r[l[a]]=r[a];
}
//e[i]表示结点i的值
//l[i]表示结点的左指针(i的上一个点的下标)
//r[i]表示结点的右指针(i的下一个点的下标)
//idx表示当前用到了哪个点(点的编号/下标)
int e[N],l[N],r[N],idx;
//初始化
void init(){
//0表示左端点,1表示右端点
r[0]=1,l[1]=0; //0号点的右边是1号点,1号点的左边是0号点
idx=2;
}
//在下标为k的点的右边插入x
void add(int k,int x){
e[idx]=x; //保存当前结点的值
r[idx]=r[k]; //将新结点的右指针指向原序列k的下一位结点
l[idx]=k; //将新结点的左指针指向k
l[r[k]]=idx; //将原序列k的下一位结点的左指针指向新结点
r[k]=idx; //将k的右指针指向新结点
}
//删除第k个点
void remove(int k){
r[l[k]]=r[k]; //将原序列k的前一个点的右指针指向k的右指针指向的值
l[r[k]]=l[k]; //将原序列k的下一个点的左指针指向k的左指针指向的值
}
题目链接:827. 双链表
2.1题目描述
实现一个双链表,双链表初始为空,支持 5 种操作:
- 在最左侧插入一个数;
- 在最右侧插入一个数;
- 将第 k 个插入的数删除;
- 在第 k 个插入的数左侧插入一个数;
- 在第 k 个插入的数右侧插入一个数
现在要对该链表进行 M 次操作,进行完所有操作后,从左到右输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数,则按照插入的时间顺序,这 n 个数依次为:第 1 个插入的数,第 2 个插入的数,…第 n 个插入的数。输入格式
第一行包含整数 M,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令可能为以下几种:
L x,表示在链表的最左端插入数 x。R x,表示在链表的最右端插入数 x。D k,表示将第 k 个插入的数删除。IL k x,表示在第 k 个插入的数左侧插入一个数。IR k x,表示在第 k 个插入的数右侧插入一个数。输出格式
共一行,将整个链表从左到右输出。
数据范围
1≤M≤100000
所有操作保证合法。输入样例:
10 R 7 D 1 L 3 IL 2 10 D 3 IL 2 7 L 8 R 9 IL 4 7 IR 2 2输出样例:
8 7 7 3 2 9
2.2思路分析
初始化:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w12V2Kpo-1687962983152)(https://note.youdao.com/yws/res/2637/WEBRESOURCEf6488ede9ec193c64633540a09c5c192)]](https://img-blog.csdnimg.cn/194a8e7c547e4400a1b3c55165467a22.png)
插入操作:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rIoqSvCE-1687962983152)(https://note.youdao.com/yws/res/2666/WEBRESOURCE3125ff04fe22c006c75d2e87bf31ef15)]](https://img-blog.csdnimg.cn/45d377e5003242109df5fda194833aa8.png)
先更新原序列k的下一个结点左指针,再修改k的右指针。否则,若颠倒,因原本k的右指针指向的便是k的下一个结点,先修改k的右指针会导致k的右结点“丢失”,再进行下续操作将无意义。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pLqVzDaf-1687962983153)(https://note.youdao.com/yws/res/2671/WEBRESOURCEac94a9e6ba7648ddf4a89d1ba389f032)]](https://img-blog.csdnimg.cn/92728d01199647668ee744f917e7f864.png)
若在k的左边插入结点,相当于在k的前一个结点的右边插入结点,所以只需实现右插入即可。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-608PyUfv-1687962983153)(https://note.youdao.com/yws/res/2688/WEBRESOURCE2684e9e3e93176edd3b9178f353855ac)]](https://img-blog.csdnimg.cn/d930cf5f0b754546bb166c1824131537.png)
删除操作:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AyGHJe0n-1687962983153)(https://note.youdao.com/yws/res/2664/WEBRESOURCE0a8623ceaf7d5a834e9acf4f730f0d6d)]](https://img-blog.csdnimg.cn/9a1484eadab2493a81c86499ccbd941b.png)
2.3代码实现
待更~
三、栈
先进后出
核心模板
//tt表示栈顶
int s[N],tt=0;
//向栈顶插入一个数
s[++tt]=x;
//从栈顶弹出一个元素
tt--;
//栈顶的值
s[tt];
//判断栈是否为空
if(tt>0){
}
题目链接:828. 模拟栈
3.1题目描述
实现一个栈,栈初始为空,支持四种操作:
push x– 向栈顶插入一个数 x;pop– 从栈顶弹出一个数;empty– 判断栈是否为空;query– 查询栈顶元素。
现在要对栈进行 M 个操作,其中的每个操作 3 和操作 4 都要输出相应的结果。输入格式
第一行包含整数 M,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令为push x,pop,empty,query中的一种。输出格式
对于每个
empty和query操作都要输出一个查询结果,每个结果占一行。
其中,empty操作的查询结果为YES或NO,query操作的查询结果为一个整数,表示栈顶元素的值。数据范围
1≤M≤100000,1≤x≤109
所有操作保证合法。
输入样例:
10 push 5 query push 6 pop query pop empty push 4 query empty输出样例:
5 5 YES 4 NO
3.2思路分析
利用数组进行模拟栈。
3.3代码实现
待更~
四、队列
先进先出
核心模板
普通队列
//在队尾插入元素,在队头弹出元素
//hh表示队头,tt表示队尾
int q[N],hh=0,tt=-1;
//向队尾插入一个数
q[++tt]=x;
//从队头弹出一个数
hh++;
//队头的值
q[hh];
//判断队列是否为空
if(hh<=tt){
}
循环队列
//hh表示队头,tt表示队尾的后一个位置
int q[N],hh=0,tt=0;
//向队尾插入一个数
q[tt++]=x;
if(tt==N) tt=0;
//从队头弹出一个数
hh++;
if(hh==N) hh=0;
//队头的值
q[hh];
//判断队列是否为空
if(hh!=tt){
}
题目链接:829. 模拟队列
4.1题目描述
实现一个队列,队列初始为空,支持四种操作:
push x– 向队尾插入一个数 x;pop– 从队头弹出一个数;empty– 判断队列是否为空;query– 查询队头元素。
现在要对队列进行 M 个操作,其中的每个操作 3 和操作 4 都要输出相应的结果。输入格式
第一行包含整数 M,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令为push x,pop,empty,query中的一种。输出格式
对于每个
empty和query操作都要输出一个查询结果,每个结果占一行。
其中,empty操作的查询结果为YES或NO,query操作的查询结果为一个整数,表示队头元素的值。数据范围
1≤M≤100000,1≤x≤109,所有操作保证合法。
输入样例:
10 push 6 empty query pop empty push 3 push 4 pop query push 6输出样例:
NO 6 YES 4
4.2思路分析
待更~
4.3代码实现
待更~
五、单调栈
核心模板
//常见模型:找出每个数左边离它最近的比它大/小的数
int tt=0;
for(int i=1;i<=n;i++){
while(tt&check(s[tt],i)) tt--;
s[++tt]=i;
}
题目链接:830. 单调栈
5.1题目描述
给定一个长度为 N 的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出 −1。
输入格式
第一行包含整数 N,表示数列长度。
第二行包含 N 个整数,表示整数数列。输出格式
共一行,包含 N 个整数,其中第 i 个数表示第 i 个数的左边第一个比它小的数,如果不存在则输出 −1。
数据范围
1≤N≤105
1≤数列中元素≤109输入样例:
5 3 4 2 7 5输出样例:
-1 3 -1 2 2
5.2思路分析
暴力求解:
每次i循环都将i前面的数入栈(从1到i-1元素入栈)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-etNqXWal-1687962983154)(https://note.youdao.com/yws/res/2821/WEBRESOURCE00818d8a952d708790baed20c25af92f)]](https://img-blog.csdnimg.cn/802c73535a814900a1d52a7dc660f9a5.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4veHLvIA-1687962983154)(https://note.youdao.com/yws/res/2819/WEBRESOURCE9b8b22767a8b6b3fc9c6790fdd250236)]](https://img-blog.csdnimg.cn/64f6a2dd83d74ea48113997c15e4cf89.png)
单调栈优化:
在暴力算法基础上,如果存在离目标值近的且小于目标值的x,且存在一个也离目标值近但是没有x离目标值近且没有x小的y,则可以去掉y(y不会被用到,因为x比y更优,将y出栈),使栈中元素为 单调上升 的序列。
5.3代码实现
#include <iostream>
#include <cstdio>
using namespace std;
const int N=100010;
int n;
int s[N],tt;
int main() {
scanf("%d",&n);
for(int i=0;i<n;i++){
int x;
scanf("%d",&x);
while(tt&&s[tt]>=x) tt--; //如果当前元素比栈顶元素小且下标比栈顶元素大,说明当前元素比栈顶元素更优,弹出栈顶元素 ;注意是while
if(tt){
printf("%d ",s[tt]);
}
else{
printf("-1 ");
}
s[++tt]=x; //将当前元素入栈
}
return 0;
}
六、单调队列
核心模板
//常见模型:找出滑动窗口中的最大值/最小值
int hh=0,tt=-1;
for(int i=0;i<n;i++){
while(hh<=tt&&check_out(q[hh])) hh++; //判断队头是否滑出窗口
while(hh<=tt&&check(q[tt],i)) t--;
q[++tt]=i;
}
题目链接:154. 滑动窗口
6.1题目描述
给定一个大小为 n≤106 的数组。
有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。你只能在窗口中看到 k 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子:
该数组为[1 3 -1 -3 5 3 6 7],k 为 3。
你的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
输入格式
输入包含两行。
第一行包含两个整数 n 和 k,分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数,代表数组的具体数值。同行数据之间用空格隔开。输出格式
输出包含两个。
第一行输出,从左至右,每个位置滑动窗口中的最小值。
第二行输出,从左至右,每个位置滑动窗口中的最大值。输入样例:
8 3 1 3 -1 -3 5 3 6 7输出样例:
-1 -3 -3 -3 3 3 3 3 5 5 6 7
6.2思路分析
最小值(用 队列 维护):如果存在在窗口中存在最小值,而且在最小值位置之前存在比它大的数,则这些数一定不会作为答案输出,可以去掉,即使队列中的元素始终是 单调上升 的。
最大值求法类似。
6.3代码实现
#include <iostream>
using namespace std;
const int N=1000010;
int n,k;
int a[N],q[N]; //q[]模拟队列,存储下标
int main() {
cin>>n>>k;
for(int i=0;i<n;i++){
cin>>a[i];
}
//求最小值
int hh=0,tt=-1;
for(int i=0;i<n;i++){
//判断队头是否已经滑出窗口
if(hh<=tt&&i-k+1>q[hh]){
hh++;
}
//如果队尾元素比当前元素大,则去掉队尾元素
while(hh<=tt&&a[q[tt]]>=a[i]){
tt--;
}
q[++tt]=i; //把当前元素下标入队
if(i>=k-1){
cout<<a[q[hh]]<<" ";
}
}
cout<<endl;
//求最大值
hh=0,tt=-1;
for(int i=0;i<n;i++){
//判断队头是否已经滑出窗口
if(hh<=tt&&i-k+1>q[hh]){
hh++;
}
//如果队尾元素比当前元素小,则去掉队尾元素
while(hh<=tt&&a[q[tt]]<=a[i]){
tt--;
}
q[++tt]=i; //把当前元素下标入队
if(i>=k-1){
cout<<a[q[hh]]<<" ";
}
}
return 0;
}
七、KMP算法
核心模板
//s[]是长文本,p是模式串,n是s的长度,m是p的长度
//求模式串的next数组:
for(int i=2,j=0;i<=m;i++){
while(j&&p[i]!=p[j+1]) j=ne[j];
if(p[i]==p[j+1]) j++;
ne[i]=j;
}
//匹配
for(int i=1,j=0;i<=n;i++){
while(j&&s[i]!=p[j+1]) j=ne[j];
if(s[i]==p[j+1]) j++;
if(j==m){
j=ne[j];
//匹配成功后的逻辑
}
}
题目链接:831. KMP字符串
7.1题目描述
给定一个字符串 S,以及一个模式串 P,所有字符串中只包含大小写英文字母以及阿拉伯数字。
模式串 P 在字符串 S 中多次作为子串出现。
求出 模式串 P 在字符串 S 中所有出现的位置的起始下标。输入格式
第一行输入整数 N,表示字符串 P的长度。
第二行输入字符串 P。
第三行输入整数 M,表示字符串 S的长度。
第四行输入字符串 S。输出格式
共一行,输出所有出现位置的起始下标(下标从 0开始计数),整数之间用空格隔开。
数据范围
1≤N≤105
1≤M≤106输入样例:
3 aba 5 ababa输出样例:
0 2
7.2思路分析
暴力做法:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PPcrgGSR-1687962983155)(https://note.youdao.com/yws/res/3013/WEBRESOURCEfb6865029aeac1d8240f45bf98cf8308)]](https://img-blog.csdnimg.cn/539adff1287d43b1825bdee70883d69f.png)
KMP算法:
next数组:
next[i]=j表示字符串前i个字母中从第一个字符开始长度为j的字符串与从某个位置到结尾长度为j的字符串相等,而且此长度j为最大(最长相等前后缀的长度)。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bkVOfVSi-1687962983155)(https://note.youdao.com/yws/res/2915/WEBRESOURCE96e7da5d4c145222c8b2fcb45fd1c6c1)]](https://img-blog.csdnimg.cn/61a448fafa254b51b252d6946e4f9e84.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wJu68ZuH-1687962983155)(https://note.youdao.com/yws/res/3011/WEBRESOURCEaa7a620d0db98a9580e4fb82c01a200f)]](https://img-blog.csdnimg.cn/a5c23f5187294533b04cd8dd26d2f2e6.png)
7.3代码实现
#include <iostream>
using namespace std;
const int N=100010,M=1000010;
int n,m;
char p[N],s[M];
int ne[N];
int main() {
cin>>n>>p+1>>m>>s+1;
//求next过程 next[1]=0,因为j=1不匹配时只能退到j=0
for(int i=2,j=0;i<=n;i++){ //求next数组也是根据p串来找某个位置i的最长公共前后缀
while(j&&p[i]!=p[j+1]){ //如果j没有退回起点而且当前p[i]和p[j+1]不匹配
j=ne[j]; //j退回到可以从某个字符再开始匹配的位置
}
if(p[i]==p[j+1]) j++; //如果p[i]与p[j+1]正好匹配了,公共前后缀长度为j+1
ne[i]=j; //记录此时的j
}
//KMP匹配过程
for(int i=1,j=0;i<=m;i++){ //i从1开始,j从0开始;因每次都是要来比较s[i]与p[j+1]是否相等,所以错开一位
while(j&&s[i]!=p[j+1]){ //j没有退回起点而且当前s[i]和p[j+1]不匹配
j=ne[j]; //j退到可以从某个字符再开始匹配的位置
}
if(s[i]==p[j+1]) j++; //如果s[i]和p[j+1]已经匹配,则开始比较下一个位置两字符串中字母是否相等
if(j==n){
//匹配成功
cout<<i-n<<" ";
j=ne[j]; //若匹配成功,此时j已匹配过,下次匹配ne[j]位置和原串下一个位置
}
}
return 0;
}
八、Trie树
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DiLxSi3C-1687962983155)(https://note.youdao.com/yws/res/3916/WEBRESOURCEeab75556ed7fc58e8a72facbe310db86)]](https://img-blog.csdnimg.cn/0632a122de04445ebee2c5ecee9a3180.png)
在每个单词结尾结尾做标记,说明存在以该字母结尾的单词。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QXpE6JBl-1687962983156)(https://note.youdao.com/yws/res/3920/WEBRESOURCE149f66164fd035488a44f08f6afeaa83)]](https://img-blog.csdnimg.cn/4215dc63866c44d7a0d2a8338567daa0.png)
核心模板
int son[N][26],cnt[N],idx;
//idx代表点的编号,0号点既是根结点,又是空结点
//son数组存储树中每个结点的子结点(第一维表示结点编号,第二维表示26个孩子是否有,有则存储的是子节点编号,无则存储的是0;26个字母,最多26个子结点)
//cnt数组存储以每个结点结尾的单词数量
//插入一个字符串
void insert(char *str){
int p=0;
for(int i=0;str[i];i++){
int u=str[i]-'a';
if(!son[p][u]) son[p][u]=++idx;
p=son[p][u];
}
cnt[p]++;
}
//查询字符串出现的次数
int query(char *str){
int p=0;
for(int i=0;str[i];i++){
int u=str[i]-'a';
if(!son[p][u]) return 0;
p=son[p][u];
}
return cnt[p];
}
使用string写的模板
#include <iostream>
#include <string>
using namespace std;
const int N=100010;
int son[N][26],cnt[N],idx;
void insert(string s){
int p=0;
for(int i=0;i<s.size();i++){
int u=s[i]-'a';
if(!son[p][u]) son[p][u]=++idx;
p=son[p][u];
}
cnt[p]++;
}
int query(string s){
int p=0;
for(int i=0;i<s.size();i++){
int u=s[i]-'a';
if(!son[p][u]) return 0;
p=son[p][u];
}
return cnt[p];
}
int main(){
int n;
cin>>n;
while(n--){
char op;
cin>>op;
string x;
if(op=='I'){
cin>>x;
insert(x);
}
else{
cin>>x;
cout<<query(x)<<endl;
}
}
return 0;
}
题目链接:835. Trie字符串统计
8.1题目描述
维护一个字符串集合,支持两种操作:
I x向集合中插入一个字符串 x;Q x询问一个字符串在集合中出现了多少次。共有 N 个操作,所有输入的字符串总长度不超过 105,字符串仅包含小写英文字母。输入格式
第一行包含整数 N ,表示操作数。
接下来 N 行,每行包含一个操作指令,指令为
I x或Q x中的一种。输出格式
对于每个询问指令
Q x,都要输出一个整数作为结果,表示 x 在集合中出现的次数。每个结果占一行。
数据范围
1≤N≤2∗104
输入样例:
5 I abc Q abc Q ab I ab Q ab输出样例:
1 0 1
8.2思路分析
直接套用模板即可,注意细节。
8.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
int son[N][26],cnt[N],idx;
char str[N];
void insert(char str[]){
int p=0; //初始化p从0即根结点开始
for(int i=0;str[i];i++){ //遍历字符串str
int u=str[i]-'a'; //将每个字母转换对应的0~25的下标
if(!son[p][u]) son[p][u]=++idx; //如果p所在结点没有以u所代表的字母,则将该字母作为p的子结点
p=son[p][u]; //p更新为其子节点
}
cnt[p]++; //以p结尾的单词数量加1
}
int query(char str[]){
int p=0; //初始化p从0即根结点开始
for(int i=0;str[i];i++){ //遍历字符串str
int u=str[i]-'a'; //将每个字母转换对应的0~25的下标
if(!son[p][u]) return 0; //如果p所在结点没有以u所代表的字母,说明不存在以u所代表字母结尾的单词,直接返回0
p=son[p][u]; //p更新为其子节点
}
return cnt[p]; //返回以p结尾的单词数量
}
int main(){
int n;
cin>>n;
while(n--){
char op[2];
cin>>op>>str;
if(op[0]=='I') insert(str);
else cout<<query(str)<<endl;
}
return 0;
}
九、并查集
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VEz21fYJ-1687962983156)(https://note.youdao.com/yws/res/3937/WEBRESOURCEcea31a558109a8facdfd98d894413a21)]](https://img-blog.csdnimg.cn/99d19bd0bb1349e7b25b795601ec28b1.png)
核心模板
-
朴素并查集:
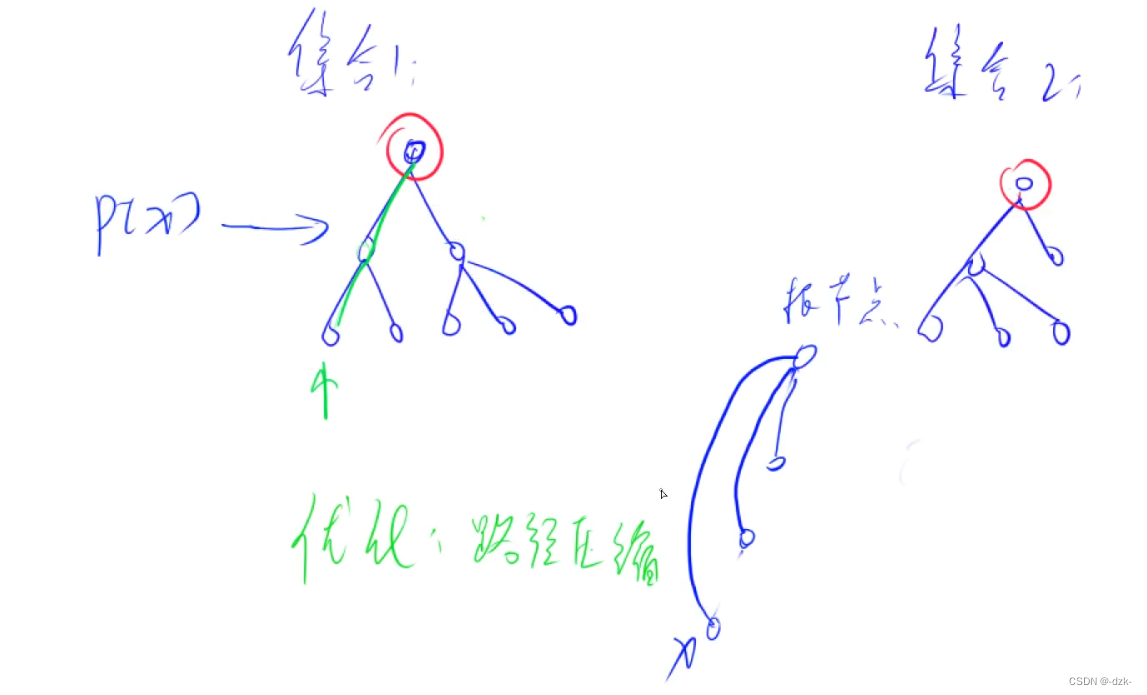
路径压缩:查找时,如果还没有找到目标值的父结点时,将路径上每个点的父结点,在向上寻找过程中更新记录。
int p[N];//存储每个点的祖宗结点
//返回x的祖宗结点
int find(int x){
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
//初始化,假定结点编号是1~n
for(int i=1;i<=n;i++){
p[i]=i;
}
//合并a和b所在的两个集合
p[find(a)]=find(b);
- 维护size的并查集
//注意size可能与某些内置变量名冲突,故改成了num
int p[N],num[N];
//p[]存储每个结点的祖宗结点,num[]只有祖宗结点有意义,表示祖宗结点所在集合中点的数量
//返回x的祖宗结点
int find(int x){
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
//初始化,假定结点编号是1~n
for(int i=1;i<=n;i++){
p[i]=i;
num[i]=1;
}
//合并a和b所在的两个集合
num[find(b)]+=num[find(a)];
p[find(a)]=find(b);
- 维护到祖宗结点距离的并查集
int p[N],d[N];
//p[]存储每个结点的祖宗结点,d[x]存储x到p[x]的距离
//返回x的祖宗结点
int find(int x){
if(p[x]!=x){
int u=find(p[x]);
d[x]+=d[p[x]];
p[x]=u;
}
return p[x];
}
//初始化,假定结点编号是1~n
for(int i=1;i<=n;i++){
p[i]=i;
d[i]=0;
}
//合并a和b所在的两个集合
p[find(a)]=find(b);
d[find(a)]=distance;//根据具体问题,初始化find(a)的偏移量
题目一
题目链接:836. 合并集合
9.1题目描述
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为
M a b或Q a b中的一种。输出格式
对于每个询问指令
Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出Yes,否则输出No。每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
4 5 M 1 2 M 3 4 Q 1 2 Q 1 3 Q 3 4输出样例:
Yes No Yes
9.2思路分析
套用模板即可,注意细节。
9.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
int n,m;
int p[N]; //存储每个结点的父结点
//返回祖宗结点+路径压缩
int find(int x){
//如果x的父结点不是根结点,就向上走一层,看x的父结点的父结点是否是根结点,直至查找到祖宗结点(根结点) ,递归返回过程中将该路径上的结点的父结点都更新成了根结点,起到了路径压缩的作用
if(p[x]!=x) p[x]=find(p[x]);
return p[x]; //返回x的父结点
}
int main(){
cin>>n>>m;
//并查集初始化 ,每个结点的父结点为自己,
for(int i=1;i<=n;i++){
p[i]=i;
}
char op;
int a,b;
while(m--){
cin>>op>>a>>b;
if(op=='M') p[find(a)]=find(b); //将a的根结点的父结点设为b的根结点
else{
if(find(a)==find(b)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
return 0;
}
题目二
题目链接:837. 连通块中点的数量
9.1题目描述
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b 可能相等;Q2 a,询问点 a 所在连通块中点的数量;输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为
C a b,Q1 a b或Q2 a中的一种。输出格式
对于每个询问指令
Q1 a b,如果 a 和 b 在同一个连通块中,则输出Yes,否则输出No。对于每个询问指令
Q2 a,输出一个整数表示点 a 所在连通块中点的数量每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
5 5 C 1 2 Q1 1 2 Q2 1 C 2 5 Q2 5输出样例:
Yes 2 3
9.2思路分析
套用模板即可,注意细节。
9.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
int n,m;
int p[N],num[N]; //p[]存储每个结点的父结点,num[]存储祖宗结点所在集合中结点个数(只有祖宗结点的num有意义)
int find(int x){
//如果x的父结点不是根结点,就向上走一层,看x的父结点的父结点是否是根结点,直至查找到祖宗结点(根结点) ,递归返回过程中将该路径上的结点的父结点都更新成了根结点,起到了路径压缩的作用
if(p[x]!=x) p[x]=find(p[x]);
return p[x]; //返回x的父结点
}
int main(){
cin>>n>>m;
//并查集初始化,每个结点的父结点为自己,每个根结点所在集合中结点数量为1
for(int i=1;i<=n;i++){
p[i]=i;
num[i]=1;
}
char op[5];
int a,b;
while(m--){
cin>>op;
if(op[0]=='C') {
cin>>a>>b;
if(find(a)!=find(b)){ //如果a、b不在一个集合中,将a所在集合中的元素数量累加进b所在集合中的元素数量中去
num[find(b)]+=num[find(a)];
}
p[find(a)]=find(b); //将a的根结点的父结点设为b的根结点
}
else if(op[1]=='1'){
cin>>a>>b;
if(find(a)==find(b)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
else{
cin>>a;
cout<<num[find(a)]<<endl;
}
}
return 0;
}
十、堆
-
堆(STL中优先队列)是一棵 完全二叉树
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lWmAOxp3-1687962983157)(https://note.youdao.com/yws/res/4306/WEBRESOURCE11bfc17d1e78ed9031bc52c96b6b7d17)]](https://img-blog.csdnimg.cn/dff23178703b4a75bba4f05476735344.png)
-
小根堆:每个结点的值都小于其左右儿子的值。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hr6voT8t-1687962983157)(https://note.youdao.com/yws/res/4311/WEBRESOURCE5511eefe5a571aaf55d635918bb8eb77)]](https://img-blog.csdnimg.cn/3346fc79d8704c2ebe256601c3b4867d.png)
-
下标从1开始,若从0开始会造成冲突。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Nt5Wly7G-1687962983157)(https://note.youdao.com/yws/res/4321/WEBRESOURCE25c525f12d0eba9e6251b72286e2aeca)]](https://img-blog.csdnimg.cn/362b8fa96aa34126bec57001dbfdba3c.png)
-
down和up操作时间复杂度 O(logn)。down和up操作均是对对应下标的值进行操作,并不是对下标进行down、up操作
-
down操作:每次与其左右儿子比较,如果比左或右儿子大,则将其中较小的交换,使其满足堆定义,否则,不交换,完成down操作。
-
up操作:每次与其父结点比较,若比父结点小,则交换,使其满足堆定义,否则不交换,意味着完成up操作。
-
建堆操作:从n/2开始,依次从下层往上层每个结点进行down操作,先完成子结点的建堆,再完成父结点的建堆,直到完成所有元素的down操作,建堆完成。
核心模板
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6SxxuiQ7-1687962983158)(https://note.youdao.com/yws/res/4355/WEBRESOURCE3ef515e3f2b1027a82ab0a2d3441b5e3)]](https://img-blog.csdnimg.cn/2cc5305a15444162913092d252357a72.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-br1tEYq6-1687962983158)(https://note.youdao.com/yws/res/4357/WEBRESOURCE2266104f5c62baaa5acbb7a7a770dc55)]](https://img-blog.csdnimg.cn/cd81306538bd4b25991768180b9e81e5.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZjWfGslO-1687962983158)(https://note.youdao.com/yws/res/4360/WEBRESOURCE5813d7b6eedc36902cd409878d9f3afe)]](https://img-blog.csdnimg.cn/c80d26e34335470cb6ba198c4ccf015b.png)
//h[N]存储堆中的值,h[1]是堆顶,x的左儿子是2x,右儿子是2x+1
//ph[k]存储第k个插入的点在堆中的位置
//hp[k]存储堆中下标是k的点是第几个插入的
//num代表堆中点的数量
int h[N],ph[N],hp[k],num;
//交换两个点及其映射关系
void heap_swap(int a,int b){
swap(ph[hp[a]],ph[hp[b]]);
swap(hp[a],hp[b]);
swap(h[a],h[b]);
}
void down(int u){
int t=u;
if(u*2<=num&&h[u*2]<h[t]) t=u*2;
if(u*2+1<=num&&h[u*2+1]<h[t]) t=u*2+1;
if(u!=t){
heap_swap(u,t);
down(t);
}
}
void up(int u){
while(u/2&&h[u]<h[u/2]){
heap_swap(u,u/2);
u>>=1;
}
}
//O(n)建堆
for(int i=n/2;i;i--) down(i);
题目一
题目链接:838. 堆排序
10.1题目描述
输入一个长度为 n 的整数数列,从小到大输出前 m 小的数。
输入格式
第一行包含整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
输出格式
共一行,包含 m 个整数,表示整数数列中前 m 小的数。
数据范围
1≤m≤n≤105 ,1≤数列中元素≤109
输入样例:
5 3 4 5 1 3 2输出样例:
1 2 3
10.2思路分析
套用模板即可,注意细节。
10.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
int n,m;
int h[N],num; //h[]存储结点的值,num存储结点个数
void down(int u){
int t=u; //t存储该结点及其左右儿子中的最小值的结点编号
if(u*2<=num&&h[u*2]<h[t]) t=u*2; //如果左儿子存在,且比该结点值小,更新t为左儿子
if(u*2+1<=num&&h[u*2+1]<h[t]) t=u*2+1; //如果右儿子也存在,且比该结点和其左儿子值小,更新t为右儿子
//如果该结点不是最小值
if(u!=t){
swap(h[u],h[t]); //将该结点换成其左右儿子中最小值
down(t); //将该结点(编号已经是t,h[t]存储该结点的值)继续与下面的点比较进行down操作
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>h[i];
}
num=n;
//建堆
for(int i=n/2;i;i--) down(i);
while(m--){
cout<<h[1]<<' ';
//删除堆顶元素
h[1]=h[num]; //用最后一个元素将堆顶元素覆盖
num--; //堆中元素个数-1
down(1); //对堆顶元素使用down操作
}
return 0;
}
题目二
题目链接:839. 模拟堆
10.1题目描述
维护一个集合,初始时集合为空,支持如下几种操作:
I x,插入一个数 x;PM,输出当前集合中的最小值;DM,删除当前集合中的最小值(数据保证此时的最小值唯一);D k,删除第 k 个插入的数;C k x,修改第 k 个插入的数,将其变为 x;
现在要进行 N 次操作,对于所有第 2 个操作,输出当前集合的最小值。输入格式
第一行包含整数 N。
接下来 N 行,每行包含一个操作指令,操作指令为
I x,PM,DM,D k或C k x中的一种。输出格式
对于每个输出指令
PM,输出一个结果,表示当前集合中的最小值。每个结果占一行。
数据范围
1≤N≤105−109≤x≤109
数据保证合法。
输入样例:
8 I -10 PM I -10 D 1 C 2 8 I 6 PM DM输出样例:
-10 6
10.2思路分析
套用模板即可,注意细节。
10.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
int n,m;
int h[N],num; //h[]存储结点的值,num存储结点个数
int ph[N],hp[N]; //ph[k]存储第k个插入的点的下标,hp[k]存储下标为k的点是第几个插入的
void heap_swap(int a,int b){
swap(ph[hp[a]],ph[hp[b]]); //交换a、b
swap(hp[a],hp[b]); //交换a、b的插入数(第几个插入)
swap(h[a],h[b]); //交换两点的值
}
void down(int u){
int t=u; //t存储该结点及其左右儿子中的最小值的结点编号
if(u*2<=num&&h[u*2]<h[t]) t=u*2; //如果左儿子存在,且比该结点值小,更新t为左儿子
if(u*2+1<=num&&h[u*2+1]<h[t]) t=u*2+1; //如果右儿子也存在,且比该结点和其左儿子值小,更新t为右儿子
//如果该结点不是最小值
if(u!=t){
heap_swap(u,t); //将该结点换成其左右儿子中最小值的结点交换
down(t); //将该结点(编号已经是t)down操作
}
}
void up(int u){
//如果该结点存在父结点,且父结点比该结点值大
while(u/2&&h[u/2]>h[u]){
heap_swap(u/2,u); //将该结点和其父结点交换
u/=2; //该结点更新为其父结点,继续向上比较
}
}
int main(){
cin>>n;
while(n--){
char op[2];
int k,x;
cin>>op;
if(op[0]=='I'){
cin>>x;
num++; //堆中元素数量+1
m++; //m代表第几个插入的数
ph[m]=num; //第m个插入的点的下标是num
hp[num]=m; //下标是num的元素是第m个插入的
h[num]=x; //下标是num的点的值是x
up(num); //对新插入的元素进行up操作
}
else if(op[0]=='P'){
cout<<h[1]<<endl; //输出堆中最小值
}
else if(op[0]=='D'&&op[1]=='M'){
heap_swap(1,num); //用最后一个元素与堆顶元素交换
num--; //堆中元素个数-1
down(1); //对堆顶元素使用down操作
}
else if(op[0]=='D'){
cin>>k;
k=ph[k]; //k记录需要down或up操作的点的下标
heap_swap(k,num); //用最后一个元素与下标为k的元素交换
num--; //堆中元素个数-1,即第k个插入的点从堆中删除
down(k),up(k); //down和up只会走一个:如果此时k比其左右儿子值大,执行down操作,否则,执行up操作
}
else{
cin>>k>>x;
k=ph[k]; //让k等于第k个插入点的下标
h[k]=x; //修改下标为k的结点的值为x
down(k),up(k); //down和up只会走一个:如果此时k比其左右儿子值大,执行down操作,否则,执行up操作
}
}
return 0;
}
- 注意:删除操作不能这样写。
else if(op[0]=='D'){
cin>>k;
heap_swap(ph[k],num); //这行可以这样写
num--;
down(ph[k]),up(ph[k]); //这行不可以,因为ph[k]的值已经在heap_swap()时改成了num,即指向的点的下标是num,而heap_swap()同时也将下标为num的点的值改成了第k个插入的点的值,而这个值已经被删除了,我们应该要down或up的是最后一个点(即与第k个点交换的那个点)。
}
原因:首先要弄清楚,我们的目的是让第k个插入的点与最后一个点交换(包括值交换,ph[]、hp[]数组的交换),然后把交换后的最后一个点删除(这时最后一个点的值已经是第k个插入的点的值了),所以只需要把堆大小-1就将“原插入的第k个点”删掉了,然后我们就需要来处理交换后的第k个插入的点,此时ph[k]存储的是最后一个插入的点的下标,而这个点的值我们由于也进行了值交换操作,这个点的值其实是存储的是第k个插入的点的值,而我们已经通过num–,来把这个点给删掉了,所以直接进行down()、up()操作就会导致错误。我们需要down()或up()的点是原来最后一个点所代表的值,也就是现在第k个插入的点的下标元素中存储的值。所以我们需要提前将这个下标来存储下来(如果不记录,要通过num来进行down()和up()操作,也会导致错误,因为num的值-1了,堆中元素已经把这个点删了,最大堆元素下标也只是num-1,所以在down()或up()操作中,也会造成错误),以便后续down()或up()操作。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AsRpkzb4-1687962983158)(https://note.youdao.com/yws/res/5569/WEBRESOURCE6b82d70ef2088311a8fd3245518b75a7)]](https://img-blog.csdnimg.cn/f89fdac286284e52ba9f5fd1d03670eb.png)
帮助理解:
- 下图为算法基础课微信群中好兄弟分享的,帮助理解,如有侵权,立即删除。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kUbnUiPD-1687962983159)(https://note.youdao.com/yws/res/5593/WEBRESOURCEdfb8a6c5ec6b34aaab972850d5d0fe65)]](https://img-blog.csdnimg.cn/2900b65c398a4cc195c0e87b6079bbf9.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nsHuJ5kk-1687962983159)(https://note.youdao.com/yws/res/5598/WEBRESOURCEd0cf283227930b8c6d0ef8b2e95467ea)]](https://img-blog.csdnimg.cn/a3781e7a552d4580a6cf034481f4b9ff.png)


十一、一般哈希
哈希:将较大范围的数映射到小范围区间内。
取模的数一般取成质数,且离2的次幂尽可能远。
-
拉链法:哈希值相同的,找对应位置,在对应位置的链表中插入该元素。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ya2eSySw-1687962983159)(https://note.youdao.com/yws/res/4522/WEBRESOURCEd21fae48cc85d505155aa8275ddf2db6)]](https://img-blog.csdnimg.cn/1850f78741d34df3a588a7ad795f6fca.png)
-
开放寻址法:哈希值相同的,找对应位置,如果该位置不空,依次向后寻找,直到找到空位即可。
-
取模的数开到题目数据范围的2~3倍。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DVubEnfX-1687962983159)(https://note.youdao.com/yws/res/4561/WEBRESOURCE4453c76b16af72c5702bc984afbe98e4)]](https://img-blog.csdnimg.cn/fc38695e66ae471a9a902c445aa19285.png)
-
memset按字节赋值,最常使用0和-1来memset初始化
-
下图作者如图,来自AcWing官网,如有侵权,立即删除。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pbcmNo2Y-1687962983159)(https://note.youdao.com/yws/res/4848/WEBRESOURCE0ed15177f00b4c7ef166243efe3fcee3)]](https://img-blog.csdnimg.cn/6129eea13b1c44f9883da8735cdd7603.png)
核心模板
- 拉链法
int h[N],e[N],ne[N],idx;
//向哈希表中插入一个数
void insert(int x){
int k=(x%N+N)%N; //N取大于区间范围的最小质数
e[idx]=x;
ne[idx]=h[k];
h[k]=idx++;
}
//在哈希表中查询某个数是否存在
bool find(int x){
int k=(x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i]){
if(e[i]==x){
return true;
}
}
return false;
}
- 开放寻址法
int h[N];
//如果x在哈希表中,返回x的下标;如果x不在哈希表中,返回x应该插入的位置
int find(int x){
int t=(x%N+N)%N;
while(h[t]!=null&&h[t]!=x){
t++;
if(t==N) t=0;
}
return t;
}
题目链接:840. 模拟散列表
11.1题目描述
维护一个集合,支持如下几种操作:
I x,插入一个数 x;Q x,询问数 x 是否在集合中出现过;
现在要进行 N 次操作,对于每个询问操作输出对应的结果。输入格式
第一行包含整数 N,表示操作数量。
接下来 N 行,每行包含一个操作指令,操作指令为
I x,Q x中的一种。输出格式
对于每个询问指令Q x,输出一个询问结果,如果 x 在集合中出现过,则输出Yes,否则输出No。每个结果占一行。
数据范围
1≤N≤105
−109≤x≤109
输入样例:
5 I 1 I 2 I 3 Q 2 Q 5输出样例:
Yes No
11.2思路分析
套用模板即可,注意细节。
11.3代码实现
拉链法:
#include <iostream>
#include <cstring>
using namespace std;
const int N=100003;
int h[N],e[N],ne[N],idx; //与单链表定义类似,h[]存储每个链的头结点,e[]存储每个结点的值,ne[]存储每个结点的next指针,idx代表结点编号
void insert(int x){
int k=(x%N+N)%N; //k为哈希值,先%再多+N再%N的目的:将x%N的结果为负数的转成正数
//单链表插入操作
e[idx]=x;
ne[idx]=h[k];
h[k]=idx++;
}
bool find(int x){
int k=(x%N+N)%N; //与上同
//单链表查找操作
for(int i=h[k];i!=-1;i=ne[i]){
if(e[i]==x){
return true;
}
}
return false;
}
int main(){
int n;
cin>>n;
memset(h,-1,sizeof h);
char op;
int x;
while(n--){
cin>>op>>x;
if(op=='I'){
insert(x);
}
else{
if(find(x)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
return 0;
}
开放寻址法:
#include <iostream>
#include <cstring>
using namespace std;
const int N=200003,null=0x3f3f3f3f; //null赋值为不在题目区间内的数
int h[N]; //h[]数组为哈希表
int find(int x){
int k=(x%N+N)%N; //与上种方法同
//如果x应该存储的位置不空
while(h[k]!=null&&h[k]!=x){
k++; //向后寻找位置
//如果已经找到表尾,再从表头开始找
if(k==N) k=0;
}
return k; //如果x在表中返回其位置,如果x不在表中返回其应该存储的位置
}
int main(){
int n;
cin>>n;
memset(h,0x3f,sizeof h); //memset按字节赋值,h为整型,4字节,则将每个字节赋值成了0x3f,即0x3f3f3f3f
char op;
int x;
while(n--){
cin>>op>>x;
int k=find(x); //找到x应该存储的位置
if(op=='I'){
h[k]=x; //插入x
}
else{
//如果x应该存储的位置不空,输出Yes,否则输出No
if(h[k]!=null) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
return 0;
}
十二、字符串哈希
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eiRrUWfm-1687962983160)(https://note.youdao.com/yws/res/4818/WEBRESOURCE758017c92100c576f0442500abc96be4)]](https://img-blog.csdnimg.cn/5da7355b323c4179803bd0f22ddfd157.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xLPBUuGC-1687962983160)(https://note.youdao.com/yws/res/4820/WEBRESOURCEbddd52d32514e9ebed652379d1ddce7e)]](https://img-blog.csdnimg.cn/dcb4072aa01c49258167699e9ad16246.png)
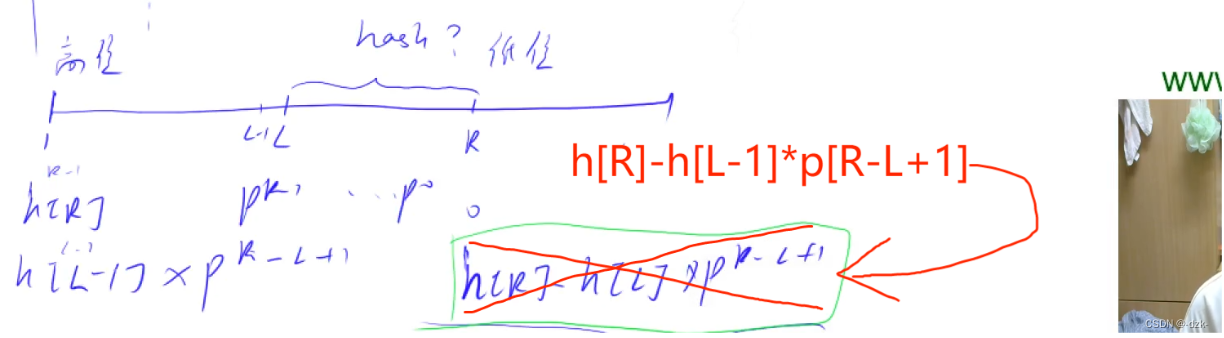
h[l-1]存储1到l-1位置子串的哈希值(子串下标从1开始),h[r]存储1到r位置子串的哈希值,要求l到r位置的哈希值:因1到l-1位置在h[l-1]和h[r]中计算哈希值时所乘权重不同(前者计算时l-1位置的权重是P0,而后者计算时r位置的权重是P0),所以要在h[r]中减去1到l-1位置的哈希值时,需要先将前l-1位置转换成在前r位置中计算时应该得到的数值(让h[l-1]乘上两者相差权重),然后再用h[r]去减去该数值。
核心思想:将字符串看成P进制数,P的经验值是131或13331,取这两个值的冲突概率低。
小技巧:取模的数用264,这样直接用unsigned long long存储,溢出的结果就是取模的结果。
核心模板
typedef unsigned long long ULL;
ULL h[N],p[N];//h[k]存储字符串前k个字母的哈希值,p[k]存储P^kmod2^64
//初始化
p[0]=1;
for(int i=1;i<=n;i++){
h[i]=h[i-1]*P+str[i];
p[i]=p[i-1]*P;
}
//计算子串str[l~r]的哈希值
ULL get(int l,int r){
return h[r]-h[l-1]*p[r-l+1];
}
题目链接:841. 字符串哈希
12.1题目描述
给定一个长度为 n 的字符串,再给定 m 个询问,每个询问包含四个整数 l1,r1,l2,r2,请你判断 [l1,r1] 和 [l2,r2] 这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。
输入格式
第一行包含整数 n 和 m,表示字符串长度和询问次数。
第二行包含一个长度为 n 的字符串,字符串中只包含大小写英文字母和数字。
接下来 m 行,每行包含四个整数 l1,r1,l2,r2 ,表示一次询问所涉及的两个区间。
注意,字符串的位置从 1 开始编号。
输出格式
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出
Yes,否则输出No。每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
8 3 aabbaabb 1 3 5 7 1 3 6 8 1 2 1 2输出样例:
Yes No Yes
12.2思路分析
套用模板即可,注意细节。
12.3代码实现
#include <iostream>
using namespace std;
typedef unsigned long long ULL;
const int N=100010,P=131;
int n,m;
char str[N];
ULL h[N],p[N]; //h[i]存储前i个字母的哈希值,p[i]存储P^i%2^64的值
//计算从l到r位置子串的哈希值
ULL get(int l,int r){
return h[r]-h[l-1]*p[r-l+1];
}
int main(){
cin>>n>>m>>str+1;
p[0]=1;
//初始化h[]和p[]
for(int i=1;i<=n;i++){
p[i]=p[i-1]*P;
h[i]=h[i-1]*P+str[i]; //P进制数,从前往后是从高位到低位,所以每一位的权重都比其后面一位的权重多1
}
while(m--){
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
if(get(l1,r1)==get(l2,r2)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}
十三、STL简介
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B5DNzVHW-1687962983160)(https://note.youdao.com/yws/res/4850/WEBRESOURCEa3f5f5287aefaefe2760ccdcfc0cb922)]](https://img-blog.csdnimg.cn/fd62fa0fbde74580889376cfccab8759.png)
- vector,变长数组,倍增思想
size() 返回元素个数
empty() 返回是否为空
clear() 清空
front()/back()
push_back()/pop_back()
begin()/end()
[]
支持比较运算,按字典序
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MRKhx53z-1687962983160)(https://note.youdao.com/yws/res/4852/WEBRESOURCE81cade64706ae5fd8c0afc137226bd07)]](https://img-blog.csdnimg.cn/19ace89847424fc8b21354b93adcef0f.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CeG0JGUe-1687962983161)(https://note.youdao.com/yws/res/4854/WEBRESOURCEf049a13978e4c8a0285fafbf8fc70f30)]](https://img-blog.csdnimg.cn/a0323a2b3f4e4514805a9bac588f4ed0.png)
- pair<int,int>(头文件
#include <utility>)
first 第一个元素
second 第二个元素
支持比较运算,以first为第一关键字,以second为第二关键字(字典序)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aSsnlJCZ-1687962983161)(https://note.youdao.com/yws/res/4856/WEBRESOURCE925f9be5a693abf0162e18e96b8b3462)]](https://img-blog.csdnimg.cn/38c4c7cb597b4caaace1d56ed30e43f7.png)
3. string(头文件#include <string>)
size()/length() 返回字符串长度
empty()
clear()
substr(起始下标,(子串长度)) 返回子串(若第二个参数省略或大于当前字符串长度,则返回整个字符串)
c_str() 返回字符串所在字符数组的起始地址
find() 查找字符第一次出现的位置,如果没有出现过返回string::npos,注意加string作用域,否则编译器不认识npos
头文件#include <string>
stoi():将字符串转化为int类型,传入string类型字符串。
atoi():将字符串转化为int类型,传入char类型字符串。
to_string():将数字常量量转化为string类型字符串。
//注意字符利用ASCII码进行过转换时(加减数字),需要强制类型转换。

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OBIcAW7i-1687962983161)(https://note.youdao.com/yws/res/4859/WEBRESOURCE7d6b9a0dba1a77148823ad4c2512654e)]](https://img-blog.csdnimg.cn/cdf8c26577bd4096885769fbaf912c49.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-txpIu0UA-1687962983161)(https://note.youdao.com/yws/res/4863/WEBRESOURCEc869c4b4bb6bdf2c1b4e3555d18955ec)]](https://img-blog.csdnimg.cn/00063e2ce06545598465e3ea3b4ddca1.png)
- queue,队列(头文件
#include <queue>)
size()
empty()
push() 向队尾插入一个元素
front() 返回队头元素
back() 返回队尾元素
pop() 弹出队头元素
新建空队列(清空队列q)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SzA0Wq7I-1687962983161)(https://note.youdao.com/yws/res/4906/WEBRESOURCEdf9e596838dc1a5758f5020725279185)]](https://img-blog.csdnimg.cn/e9c9ffe902194c33ae723bb5d77ebfd6.png)
- priority_queue,优先队列,默认是大根堆(头文件
#include <queue>)
size()
empty()
push() 插入一个元素
top() 返回堆顶元素
pop() 弹出堆顶元素
定义成小根堆的方式:priority_queue<int,vector<int>,greater<int>>q;
(也可以将正数变成相反数插入堆,得到的便是每个元素是负数的小根堆,需要操作时,取出元素加负号就是原序列的元素)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-baQLlWKj-1687962983162)(https://note.youdao.com/yws/res/4913/WEBRESOURCE47208fd2a4fc995133cb183c7fd10f53)]](https://img-blog.csdnimg.cn/6542e6754e2543d29accb1c549483c55.png)
6. stack,栈(头文件#include <stack>)
size()
empty()
push() 向栈顶插入一个元素
top() 返回栈顶元素
pop() 弹出栈顶元素
- deque,双端队列(头文件
#include <deque>)
size()
empty()
clear()
front()/back()
push_back()/pop_back()
push_front()/pop_front()
begin()/end()
[]
- set,map,multiset,multimap,基于平衡二叉树(红黑树),动态维护有序序列,set、map去重,multise、multimap不去重(头文件
#include <set>、#include <map>)
size()
empty()
clear()
begin()/end()
++,--返回前驱和后继,时间复杂度O(logn)
有重复元素,map不会插入新元素,所以旧元素不会被覆盖更新
- set/multiset(头文件
#include <set>)
insert() 插入一个数
find() 查找一个数,如果找到返回该数第一次出现的位置的迭代器,否则返回容器尾迭代
count() 返回某一个数的个数
erase()
(1)输入是一个数x,删除所有x O(k+logn)(k为x的个数)
(2)输入一个迭代器,删除这个迭代器
lower_bound()/upper_bound()
lower_bound(x) 返回大于等于x的最小的数的迭代器
upper_bound(x) 返回大于x的最小的数的迭代器

10. map/multimap(头文件#include <map>)
insert() 插入的数是一个pair
erase() 输入的参数是pair或者迭代器
find() 同上
[] 注意multimap不支持此操作。时间复杂度O(logn)
lower_bound()/upper_bound()

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6kNp8xIb-1687962983162)(https://note.youdao.com/yws/res/4998/WEBRESOURCE2bda4d316bdec6638c5a3347f3d6bc89)]](https://img-blog.csdnimg.cn/154a9c610ccb44e6a2ee684752a556fe.png)

- unordered_set,unordered_map,unordered_multiset,unordered_multimap,哈希表(头文件
#include <unordered_set>、#include <unordered_map>)
和上面类似,增删改查的时间复杂度为O(1)
不支持 lower_bound()/upper_bound(),迭代器的++,--
- bitset,压位(头文件
#include <bitset>)
bitset<10000> s;
~,&,|,^
>>,<<
==,!=
[]
count() 返回有多少个1
any() 判断是否至少有一个1
none() 判断是否全为0
set() 把所有位置成1
set(k,v) 把第k位变成v
reset() 把所有位变成0
flip() 等价于~
flip(k) 把第k位取反
- 下图来自网络,如有侵权,立即删除。

- 下图来源这里,如有侵权,立即删除。
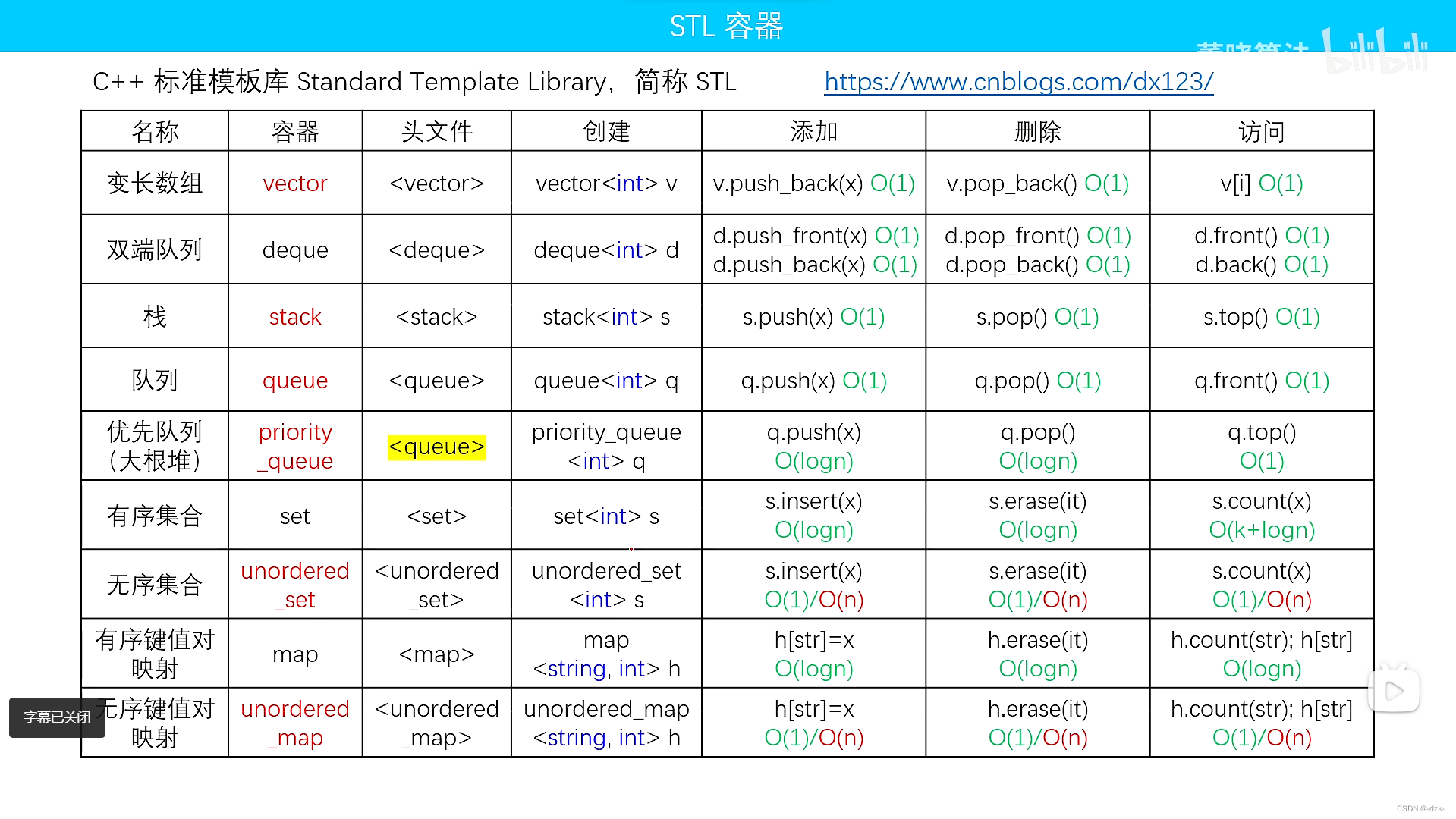
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-44z4qV1Y-1687962983154)(https://note.youdao.com/yws/res/2882/WEBRESOURCE12ca4ec9acbcfdea83236125e63790b7)]](https://img-blog.csdnimg.cn/bac14bcb5fce4e40b17fa2214bc1fa28.png)