基于粒子群算法的无约束优化问题求解
- 1 引言
- 2 粒子群算法
- 2.1 粒子群优化原理
- 2.2 粒子群算法寻优策略与参数控制
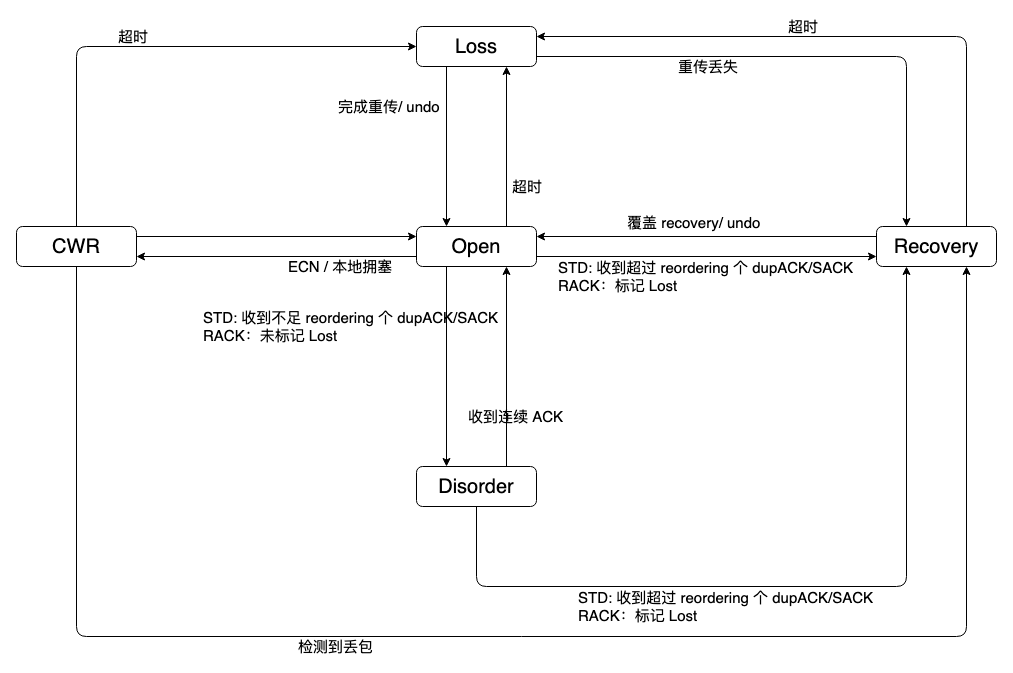
- 粒子群算法流程
- 3 粒子群算法求解无约束优化问题
- 3.1 粒子群算法求解Sphere函数(单峰测试函数)
- 3.2 Schwefel's Problem 2.26(多峰测试函数)
- 3.3 Rastrigin's Function(多峰测试函数)
- 3.4 Griewank's Function(多峰测试函数)
- 4 参考
1 引言
粒子群算法(Particle Swarm Optimization,PSO)是由美国心理学家James Kennedy和电气工程师Russell Eberhart于1995年提出的一种算法,算是比较老也是非常经典的算法之一。
PSO是非常适合于连续领域问题优化的算法,且已经在此取得相当成功的应用。 离散版本改进将PSO运用到离散领域(组合优化)之中12,如TSP、CVRP问题。
在连续优化问题中,无约束优化问题除了可以用梯度下降算法,牛顿法,共轭梯度等算法,智能优化算法因其寻优速度快,全局收敛等特点,也得到了广泛应用。
2 粒子群算法
2.1 粒子群优化原理
将问题搜索空间类比于鸟类的飞行空间,每一只鸟抽象为一个无质量的粒子(Particle),用于表征一个候选解,食物表征为最优解。优化寻求最优解的过程等同于鸟群觅食的过程,鸟群快速找到食物的一个有效方法就是搜寻目前离食物最近的同伴的位置。因此每个粒子都有速度和位置两个属性,粒子通过权衡自身经验(本身找到的最优解pbest)和群体经验(整个整群的最优解gbest)来迭代更新自己,找到最优解。


鸟类寻优过程中,沿自身飞行方向寻找食物的同时,会根据自身经验和鸟群间信息共享,调整自己的位置和速度,以期找到最优解。
2.2 粒子群算法寻优策略与参数控制
粒子按速度更新公式(1)和位置更新公式(2)寻找最优解:
v
i
j
←
ω
v
i
j
+
c
1
r
1
(
p
b
e
s
t
i
j
−
x
i
j
)
+
c
2
r
2
(
g
b
e
s
t
j
−
x
i
j
)
x
i
j
←
x
i
j
+
v
i
j
\begin{align} v_{i}^j &\leftarrow \omega v_{i}^j+c_1r_1(pbest_{i}^j-x_{i}^j)+c_2r_2(gbest^j-x_{i}^j) \\ x_{i}^j &\leftarrow x_{i}^j+v_{i}^j \end{align}
vijxij←ωvij+c1r1(pbestij−xij)+c2r2(gbestj−xij)←xij+vij
其中,
- D D D——代表搜索空间为D维(即为自变量的个数)。 j j j粒子维度索引, j = 1 , 2 , . . . , D j=1,2,...,D j=1,2,...,D。
- x i x_{i} xi——代表第 i i i个粒子的位置(即为一个解), x i = ( x i 1 , x i 2 , . . . , x i j , . . . , x i D ) x_{i}=(x_{i}^1,x_{i}^2,...,x_{i}^j,...,x_{i}^D) xi=(xi1,xi2,...,xij,...,xiD)。
- v i v_{i} vi——代表第 i i i个粒子的速度, v i = ( v i 1 , v i 2 , . . . , v i j , . . . , v i D ) v_{i}=(v_{i}^1,v_{i}^2,...,v_{i}^j,...,v_{i}^D) vi=(vi1,vi2,...,vij,...,viD)。
- p b e s t i pbest_{i} pbesti——代表粒子 i i i在搜索到的最优位置, v i = ( p b e s t i 1 , p b e s t i 2 , . . . , p b e s t i j , . . . , p b e s t i D ) v_{i}=(pbest_{i}^1,pbest_{i}^2,...,pbest_{i}^j,...,pbest_{i}^D) vi=(pbesti1,pbesti2,...,pbestij,...,pbestiD)。
- g b e s t j gbest^{j} gbestj——整个鸟群搜索到的最优位置。 g b e s t j gbest^{j} gbestj和 p b e s t i j pbest_{i}^j pbestij关系为: g b e s t j = min { p b e s t i j } j = 1 D gbest^{j}= \min \{pbest_{i}^j\}_{j=1}^D gbestj=min{pbestij}j=1D
- ω \omega ω——惯性权重(inertia weight),动态调整惯性权重可以平衡收敛的全局性和收敛速度。 ω \omega ω越大,探索新区域的能力越强,有利于全局搜索,跳出局部最优; ω \omega ω越小,逐渐退化成爬山算法,有利于算法收敛。推荐取值范围 ω ∈ [ 0.4 , 2 ] \omega \in [0.4,2] ω∈[0.4,2],另有实验表明 ω = 0.7298 \omega=0.7298 ω=0.7298时,算法有较好的收敛性能。
- c 1 c_1 c1——加速系数,表征粒子个体的经验,该值越大,证明鸟群在寻找食物过程中,越倾向于根据自己的经验知识寻找食物;该值越小,表示不注重自己的经验,鸟在寻找食物过程中“随大流、从众”。
-
c
2
c_2
c2——加速系数,表征整个鸟群的经验知识,该值越大,越注重鸟之间的信息共享;该值越小,鸟之间没有信息交流,算法演变为随机探索,导致算法收敛速度缓慢。
实验表明, c 1 = c 2 = 1.479 c_1=c_2=1.479 c1=c2=1.479时算法有较好的收敛性能。 - maxVelocity——最大速度。该参数在上述公式没有体现,为了平衡算法的探索能力与开发能力,需要设定一个合理的速度范围,限制粒子的最大速度,即粒子下一步迭代可以移动的最大距离。maxVelocity越大,粒子飞行速度快,探索能力强,但粒子容易飞过最优解;maxVelocity越小,飞行速度慢,开发能力强,但是收敛速度慢,且容易陷入局部最优解;一般为对应变量取值范围的10~20%,可根据实际情况调试,但不能大于粒子(解)的变化范围3。
粒子群算法流程
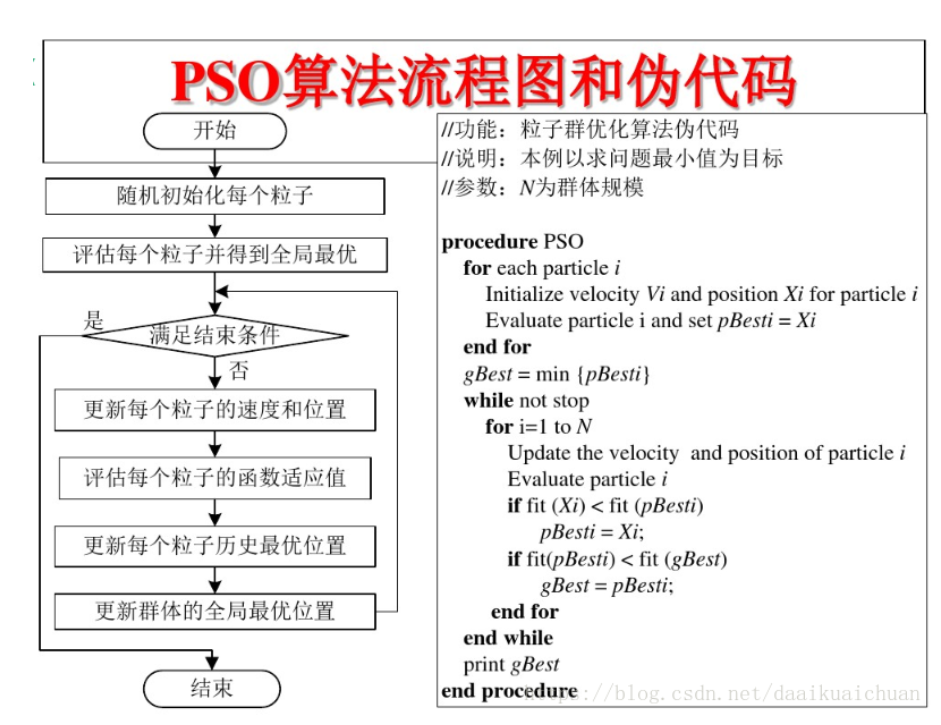
- 初始化:算法最大迭代次数MAXGEN;每个粒子的位置x和速度v;位置限制边界xMin≤ x ≤xMax,即自变量取值范围;最大速度限制,根据经验设置最大速度maxVelocity,一般为对应变量取值范围的10~20%3。
- 评估每个粒子(计算目标函数值和适应度)。
- 更新粒子的速度v和位置x
- 判断是否越界。速度越界和位置越界都需要判断。看了网上很多博客及程序,有的程序没有进行越界判断,有的只有速度越界判断45,有的则进行了速度越界和位置越界判断67。自己进行编程发现:对于单峰测试函数,没有越界判断依然能够得出最优解。
- 评估每个粒子(计算目标函数值和适应度)。
- 更新粒子的历史最优位置pbest
- 更新全局最优位置gbest
3 粒子群算法求解无约束优化问题
为了验证粒子群算法的求解性能,分别采用了单峰测试函数和多峰测试函数进行试验。便编程时,只需定义一个抽象的问题类Problem,使不同的测试函数继承
Problem,每次进行PSO求解时,只需传入不同的测试函数即可,降低了代码的耦合性。基于粒子群算法的无约束优化问题求解(Java)
3.1 粒子群算法求解Sphere函数(单峰测试函数)
Sphere函数8除了全局极小值外,还有d(维度)个局部极小值。呈连续、下凹、单峰,该问题的维度是 n=30,函数解为
f
(
x
1
,
x
2
,
.
.
.
,
x
30
)
=
f
(
0
,
0
,
.
.
.
,
0
)
=
0
f(x_1,x_2,...,x_{30})=f(0,0,...,0)=0
f(x1,x2,...,x30)=f(0,0,...,0)=0。
min
f
(
x
)
=
∑
i
=
1
30
x
i
2
,
−
100
≤
x
i
≤
100
\min f(x) = \sum_{i=1}^{30} x_i^2,\quad -100 \leq x_i \leq 100
minf(x)=i=1∑30xi2,−100≤xi≤100
求解结果:
全局最优解:0.00 0.00 -0.00 0.00 -0.00 0.00 -0.00 -0.00 0.00 -0.00 -0.00 -0.00 -0.00 0.00 0.00 -0.00 -0.00 0.00 -0.00 0.00 -0.00 0.00 -0.00 0.00 0.00 0.00 0.00 0.00 -0.00 -0.00
全局极小值:0.00
目标函数收敛图:

3.2 Schwefel’s Problem 2.26(多峰测试函数)
Schwefel’s函数是一个典型的欺骗问题,有1个全局极小值点,距离另一个局部最优点很远,因此如果陷入局部最优就很难跳出。Schwefel’s函数的表达式为如下。该问题的维度是 n=30,函数有全局最小值,解为 f ( x 1 , x 2 , . . . , x 30 ) = f ( 420.9687 , 420.9687 , . . . , 420.9687 ) = − 12569.5 f(x_1,x_2,...,x_{30})=f(420.9687,420.9687,...,420.9687)=-12569.5 f(x1,x2,...,x30)=f(420.9687,420.9687,...,420.9687)=−12569.5。
min f ( x ) = − ∑ i = 1 30 x i sin ( ∣ x ∣ ) , − 500 ≤ x i ≤ 500 \min f(x) = -\sum_{i=1}^{30} x_i \sin(\sqrt{|x|}), \quad -500 \leq x_i \leq 500 minf(x)=−i=1∑30xisin(∣x∣),−500≤xi≤500
3.3 Rastrigin’s Function(多峰测试函数)
Rastrigin’s 函数8有许多局部极小值。它是高度多模态的,但极小值的位置是规则分布的。该问题的维度是 n=30,函数解为 f ( x 1 , x 2 , . . . , x 30 ) = f ( 0 , 0 , . . . , 0 ) = 0 f(x_1,x_2,...,x_{30})=f(0,0,...,0)=0 f(x1,x2,...,x30)=f(0,0,...,0)=0。
min f ( x ) = ∑ i = 1 30 [ x i 2 − 10 cos ( 2 π x i ) + 10 ] , − 5.12 ≤ x i ≤ 5.12 \min f(x) = \sum_{i=1}^{30} [x_i^2-10 \cos(2\pi x_i)+10], \quad -5.12 \leq x_i \leq 5.12 minf(x)=i=1∑30[xi2−10cos(2πxi)+10],−5.12≤xi≤5.12
3.4 Griewank’s Function(多峰测试函数)
Griewank函数具有许多的局部极小值,这些极小值是规则分布的。。该问题的维度是 n=30,函数解为 f ( x 1 , x 2 , . . . , x 30 ) = f ( 0 , 0 , . . . , 0 ) = 0 f(x_1,x_2,...,x_{30})=f(0,0,...,0)=0 f(x1,x2,...,x30)=f(0,0,...,0)=0。
min f ( x ) = 1 4000 ∑ i = 1 30 x i 2 − ∏ i = 1 30 cos ( x i i ) + 10 ] , − 600 ≤ x i ≤ 600 \min f(x) = \frac{1}{4000}\sum_{i=1}^{30} x_i^2 -\prod_{i=1}^{30} \cos(\frac{x_i}{ \sqrt{i}})+10], \quad -600 \leq x_i \leq 600 minf(x)=40001i=1∑30xi2−i=1∏30cos(ixi)+10],−600≤xi≤600
4 参考
Shi X H, Liang Y C, Lee H P, et al. Particle swarm optimization-based algorithms for TSP and generalized TSP[J/OL]. Information Processing Letters, 2007, 103(5): 169-176. https://doi.org/10.1016/j.ipl.2007.03.010. ↩︎
Wei-Neng Chen, Jun Zhang, Chung H S H, et al. A Novel Set-Based Particle Swarm Optimization Method for Discrete Optimization Problems[J/OL]. IEEE Transactions on Evolutionary Computation, 2010, 14(2): 278-300. https://doi.org/10.1109/TEVC.2009.2030331. ↩︎
粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读 ↩︎ ↩︎
用python3实现粒子群优化算法 ↩︎
粒子群(PSO)算法概念及代码实现 ↩︎
粒子群算法原理及实现 ↩︎
粒子群算法Particle Swarm Optimization超详细解析+代码实例讲解 ↩︎
23种标准测试函数解析 ↩︎ ↩︎