初识Go语言25-数据结构与算法【堆、Trie树、用go中的list与map实现LRU算法、用go语言中的map和堆实现超时缓存】

文章目录

- 堆
- Trie树
- - 练习-用go中的list与map实现LRU算法
  - 练习-用go语言中的map和堆实现超时缓存

堆

堆是一棵二叉树。大根堆即任意节点的值都大于等于其子节点。反之为小根堆。
用数组来表示堆，下标为 i 的结点的父结点下标为(i-1)/2，其左右子结点分别为 (2i + 1)、(2i + 2)。

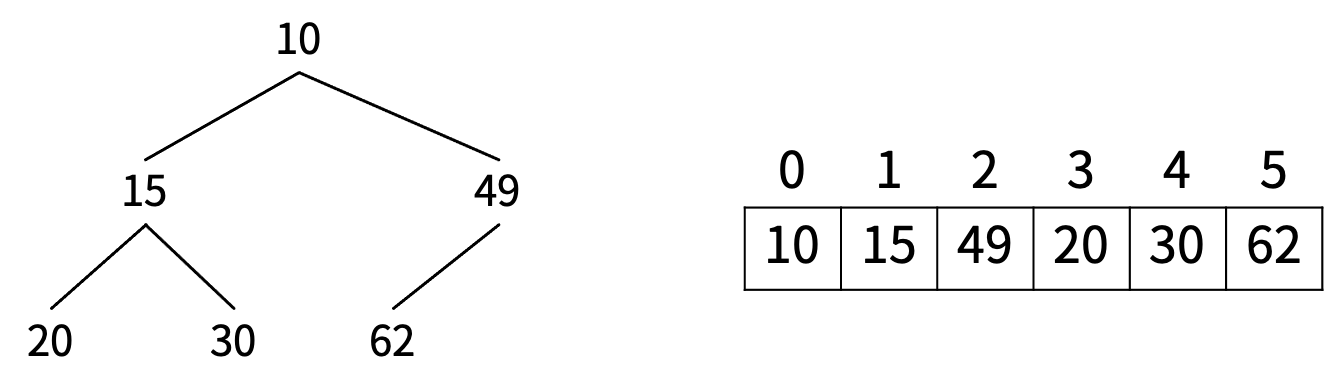
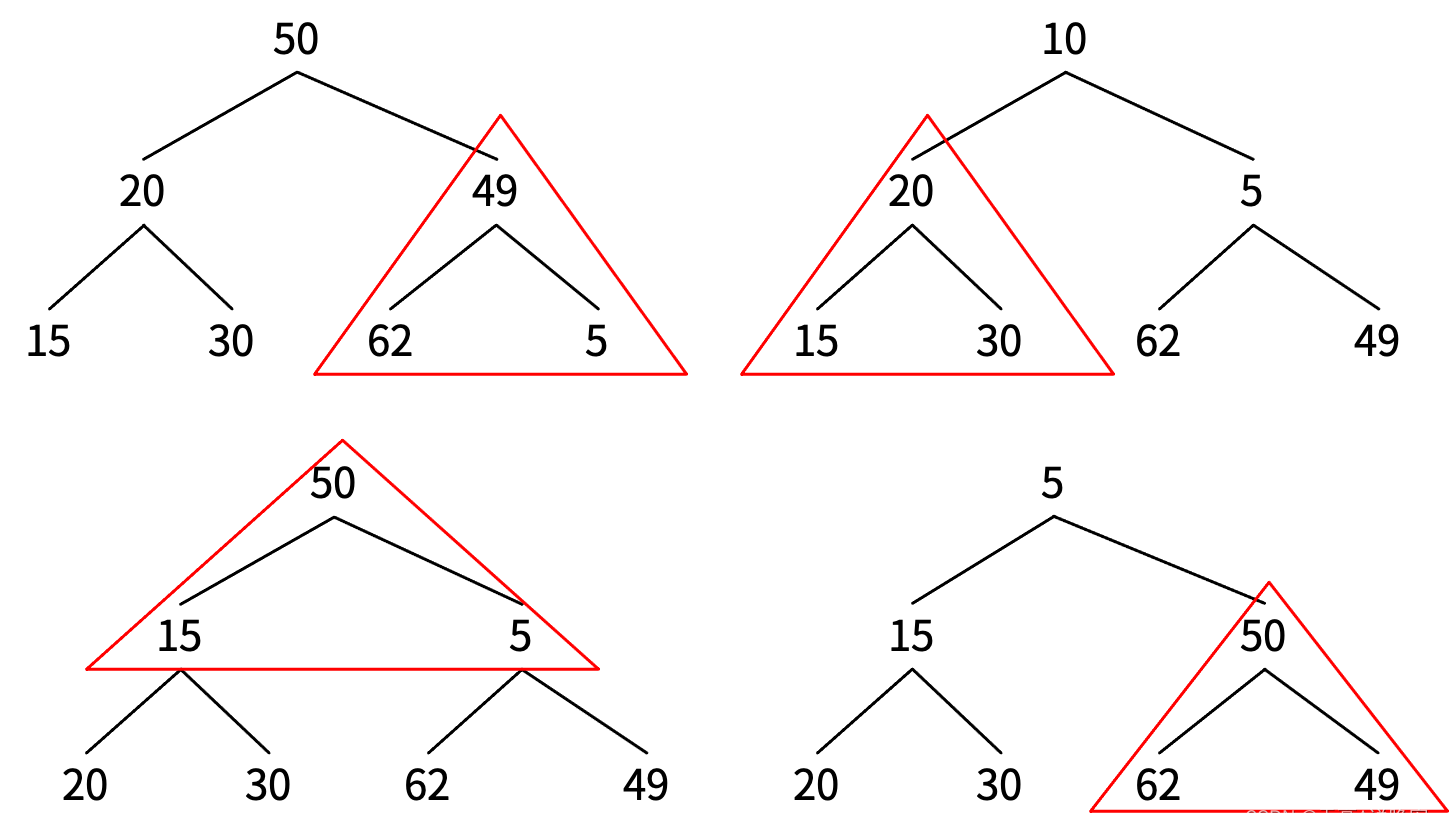
在这里插入图片描述

构建堆

在这里插入图片描述

package main

import "fmt"

//AdjustTraingle 如果只是修改slice里的元素，不需要传slice的指针；如果要往slice里append或让slice指向新的子切片，则需要传slice指针
func AdjustTraingle(arr []int, parent int) {
	left := 2*parent + 1
	if left >= len(arr) {
		return
	}

	right := 2*parent + 2
	minIndex := parent
	minValue := arr[minIndex]
	if arr[left] < minValue {
		minValue = arr[left]
		minIndex = left
	}
	if right < len(arr) {
		if arr[right] < minValue {
			minValue = arr[right]
			minIndex = right
		}
	}
	if minIndex != parent {
		arr[minIndex], arr[parent] = arr[parent], arr[minIndex]
		AdjustTraingle(arr, minIndex) //递归。每当有元素调整下来时，要对以它为父节点的三角形区域进行调整
	}
}

func ReverseAdjust(arr []int) {
	n := len(arr)
	if n <= 1 {
		return
	}
	lastIndex := n / 2 * 2
	fmt.Println(lastIndex)
	for i := lastIndex; i > 0; i -= 2 { //逆序检查每一个三角形区域
		right := i
		parent := (right - 1) / 2
		fmt.Println(parent)
		AdjustTraingle(arr, parent)
	}
}

func buildHeap() {
	arr := []int{62, 40, 20, 30, 15, 10, 49}
	ReverseAdjust(arr)
	fmt.Println(arr)
}

每当有元素调整下来时，要对以它为父节点的三角形区域进行调整。

插入元素

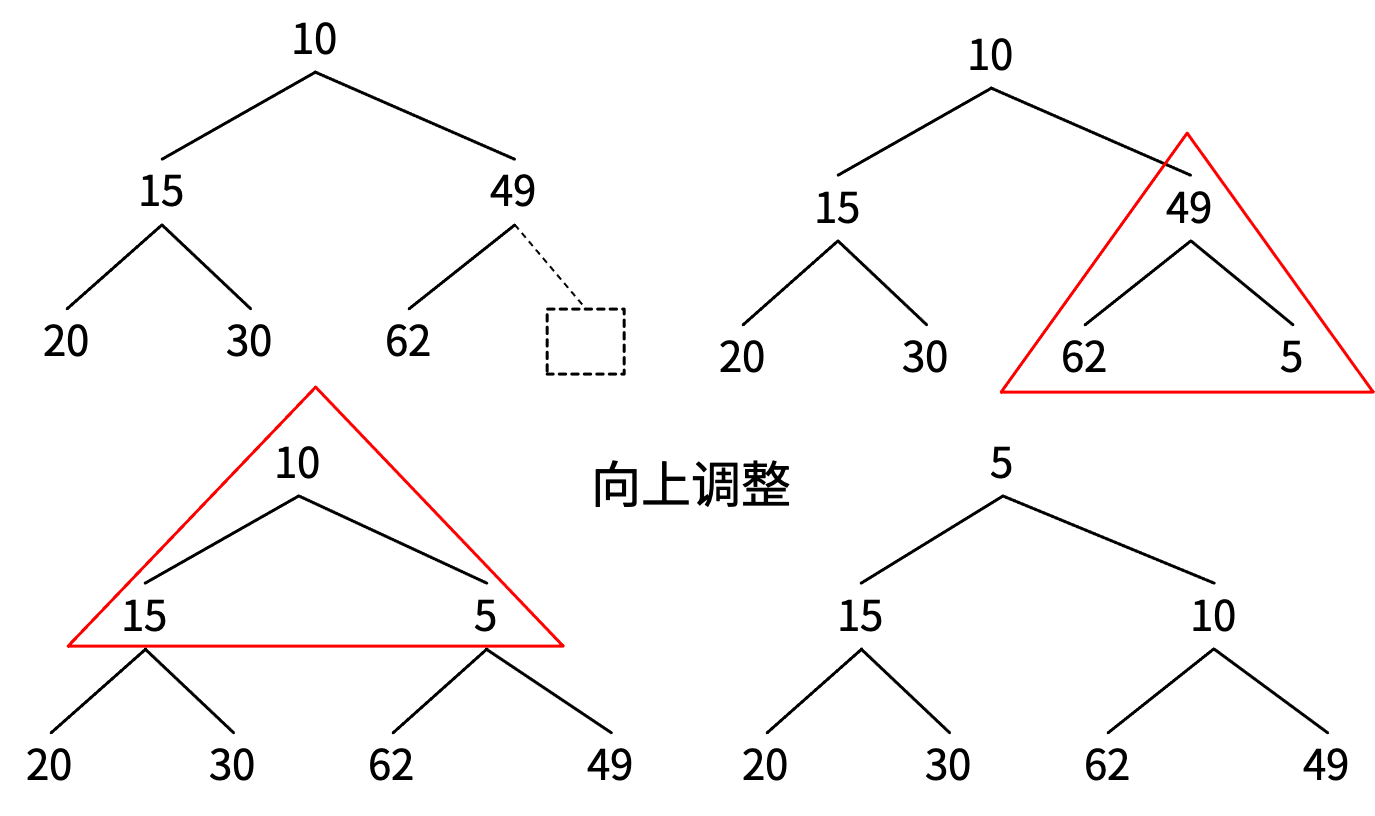
在这里插入图片描述

删除堆顶

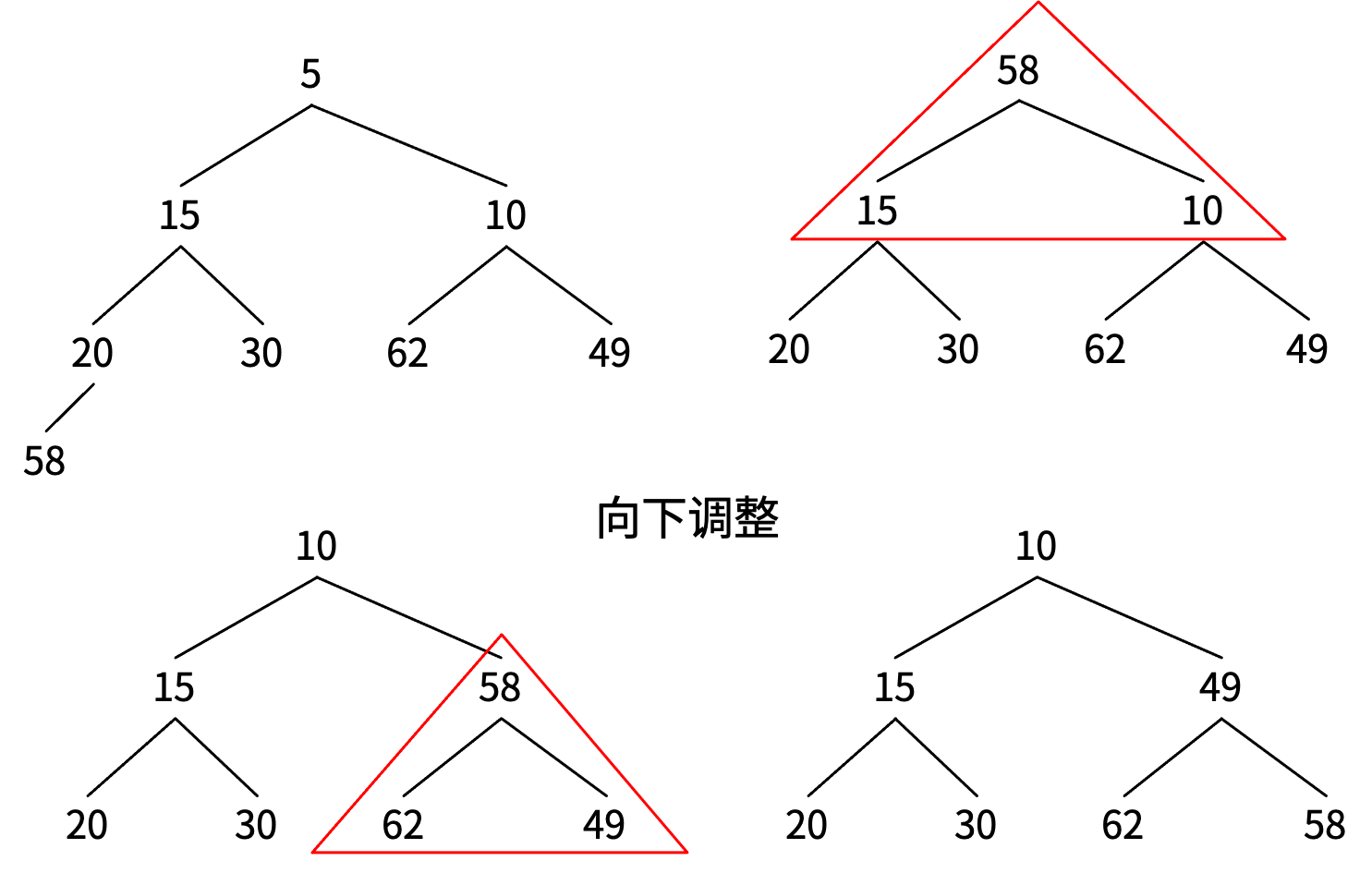
在这里插入图片描述

下面讲几个堆的应用。
堆排序

构建堆O(N)。
不断地删除堆顶O(NlogN)。

求集合中最大的K个元素

用集合的前K个元素构建小根堆。
逐一遍历集合的其他元素，如果比堆顶小直接丢弃；否则替换掉堆顶，然后向下调整堆。

把超时的元素从缓存中删除

按key的到期时间把key插入小根堆中。
周期扫描堆顶元素，如果它的到期时间早于当前时刻，则从堆和缓存中删除，然后向下调整堆。
golang中的container/heap实现了小根堆，但需要自己定义一个类，实现以下接口：

Len() int
Less(i, j int) bool
Swap(i, j int)
Push(x interface{})
Pop() x interface{}

type Item struct {
	Value    string
	priority int //优先级，数字越大，优先级越高
}

type PriorityQueue []*Item

func (pq PriorityQueue) Len() int {
	return len(pq)
}

func (pq PriorityQueue) Less(i, j int) bool {
	return pq[i].priority > pq[j].priority //golang默认提供的是小根堆，而优先队列是大根堆，所以这里要反着定义Less。定义的是大根堆
}

func (pq PriorityQueue) Swap(i, j int) {
	pq[i], pq[j] = pq[j], pq[i]
}

//往slice里append,需要传slice指针
func (pq *PriorityQueue) Push(x interface{}) {
	item := x.(*Item)
	*pq = append(*pq, item)
}

//让slice指向新的子切片，需要传slice指针
func (pq *PriorityQueue) Pop() interface{} {
	old := *pq
	n := len(old)
	item := old[n-1]   //数组最后一个元素
	*pq = old[0 : n-1] //去掉最一个元素
	return item
}
func testPriorityQueue() {
	pq := make(PriorityQueue, 0, 10)
	pq.Push(&Item{"A", 3})
	pq.Push(&Item{"B", 2})
	pq.Push(&Item{"C", 4})
	heap.Init(&pq)
	heap.Push(&pq, &Item{"D", 6})
	for pq.Len() > 0 {
		fmt.Println(heap.Pop(&pq))
	}
}
//&{D 6}
//&{C 4}
//&{A 3}
//&{B 2}

Trie树

trie树又叫字典权。
现有term集合：{分散，分散精力，分散投资，分布式，工程，工程师}，把它们放到Trie树里如下图:

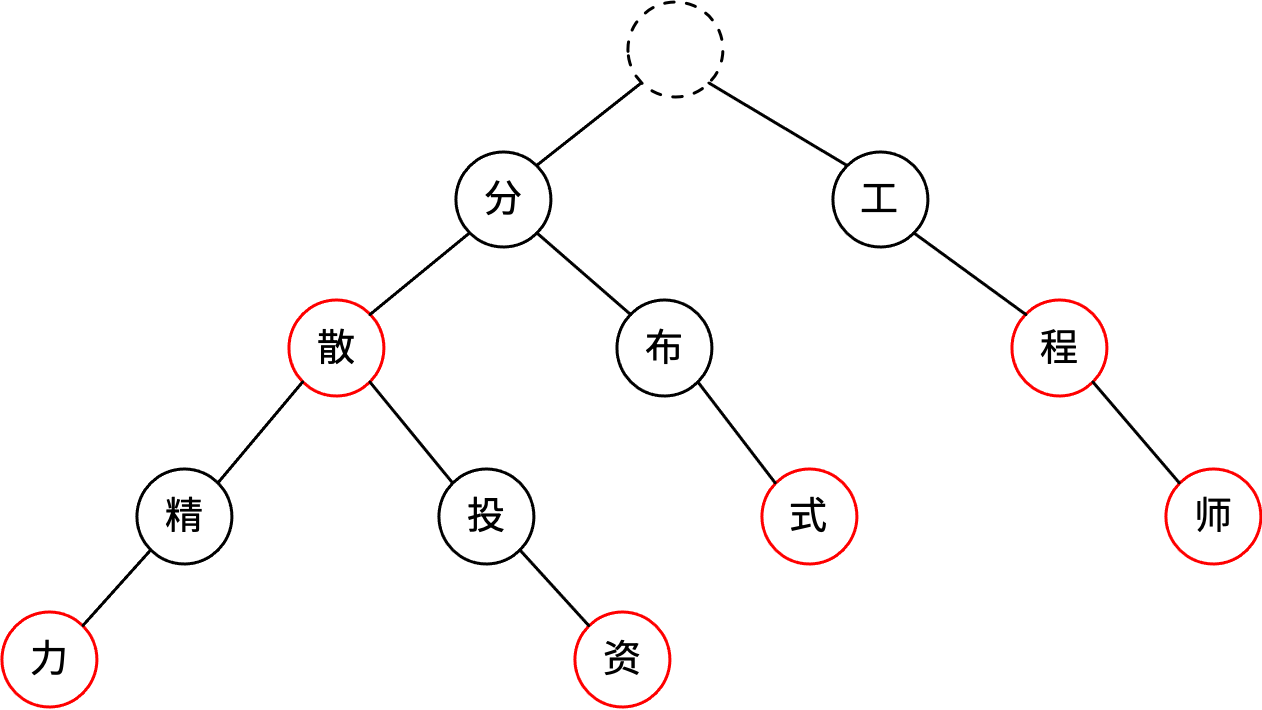
在这里插入图片描述

Trie树的根节点是总入口，不存储字符。对于英文，第个节点有26个子节点，子节点可以存到数组里；中文由于汉字很多，用数组存子节点太浪费内存，可以用map存子节点。从根节点到叶节点的完整路径是一个term。从根节点到某个中间节点也可能是一个term，即一个term可能是另一个term的前缀。上图中红圈表示从根节点到本节点是一个完整的term。

package main

import "fmt"

type TrieNode struct {
	Word     rune               //当前节点存储的字符。byte只能表示英文字符，rune可以表示任意字符
	Children map[rune]*TrieNode //孩子节点，用一个map存储
	Term     string
}

type TrieTree struct {
	root *TrieNode
}

//add 把words[beginIndex:]插入到Trie树中
func (node *TrieNode) add(words []rune, term string, beginIndex int) {
	if beginIndex >= len(words) { //words已经遍历完了
		node.Term = term
		return
	}

	if node.Children == nil {
		node.Children = make(map[rune]*TrieNode)
	}

	word := words[beginIndex] //把这个word放到node的子节点中
	if child, exists := node.Children[word]; !exists {
		newNode := &TrieNode{Word: word}
		node.Children[word] = newNode
		newNode.add(words, term, beginIndex+1) //递归
	} else {
		child.add(words, term, beginIndex+1) //递归
	}
}

//walk words[0]就是当前节点上存储的字符，按照words的指引顺着树往下走，最终返回words最后一个字符对应的节点
func (node *TrieNode) walk(words []rune, beginIndex int) *TrieNode {
	if beginIndex == len(words)-1 {
		return node
	}
	beginIndex += 1
	word := words[beginIndex]
	if child, exists := node.Children[word]; exists {
		return child.walk(words, beginIndex)
	} else {
		return nil
	}
}

//traverseTerms 遍历一个node下面所有的term。注意要传数组的指针，才能真正修改这个数组
func (node *TrieNode) traverseTerms(terms *[]string) {
	if len(node.Term) > 0 {
		*terms = append(*terms, node.Term)
	}
	for _, child := range node.Children {
		child.traverseTerms(terms)
	}
}

func (tree *TrieTree) AddTerm(term string) {
	if len(term) <= 1 {
		return
	}
	words := []rune(term)

	if tree.root == nil {
		tree.root = new(TrieNode)
	}

	tree.root.add(words, term, 0)
}

func (tree *TrieTree) Retrieve(prefix string) []string {
	if tree.root == nil || len(tree.root.Children) == 0 {
		return nil
	}
	words := []rune(prefix)
	firstWord := words[0]
	if child, exists := tree.root.Children[firstWord]; exists {
		end := child.walk(words, 0)
		if end == nil {
			return nil
		} else {
			terms := make([]string, 0, 100)
			end.traverseTerms(&terms)
			return terms
		}
	} else {
		return nil
	}
}

func main() {
	tree := new(TrieTree)
	tree.AddTerm("分散")
	tree.AddTerm("分散精力")
	tree.AddTerm("分散投资")
	tree.AddTerm("分布式")
	tree.AddTerm("工程")
	tree.AddTerm("工程师")

	terms := tree.Retrieve("分散")
	fmt.Println(terms)
	terms = tree.Retrieve("人工")
	fmt.Println(terms)
}

练习-用go中的list与map实现LRU算法

type LRUCache struct {
	cache map[int]int
	lst   list.List
	Cap   int // 缓存容量上限
}

func NewLRUCache(cap int) *LRUCache {
	lru := new(LRUCache)
	lru.Cap = cap
	lru.cache = make(map[int]int, cap)
	lru.lst = list.List{}
	return lru
}

func (lru *LRUCache) Add(key, value int) {
	if len(lru.cache) < lru.Cap { //还未达到缓存的上限
		// 直接把key value放到缓存中
		lru.cache[key] = value
		lru.lst.PushFront(key)
	} else { // 缓存已满
		// 先从缓存中淘汰一个元素
		back := lru.lst.Back()
		delete(lru.cache, back.Value.(int))
		lru.lst.Remove(back)
		// 把key value放到缓存中
		lru.cache[key] = value
		lru.lst.PushFront(key)
	}
}

func (lru *LRUCache) find(key int) *list.Element {
	if lru.lst.Len() == 0 {
		return nil
	}
	head := lru.lst.Front()
	for {
		if head == nil {
			break
		}
		if head.Value.(int) == key {
			return head
		} else {
			head = head.Next()
		}
	}
	return nil
}

func (lru *LRUCache) Get(key int) (int, bool) {
	value, exists := lru.cache[key]
	ele := lru.find(key)
	if ele != nil {
		lru.lst.MoveToFront(ele)
	}
	return value, exists
}

func testLRU() {
	lru := NewLRUCache(10)
	for i := 0; i < 10; i++ {
		lru.Add(i, i) // 9 8 7 6 5 4 3 2 1 0
	}

	for i := 0; i < 10; i += 2 {
		lru.Get(i) // 8 6 4 2 0 9 7 5 3 1
	}

	for i := 10; i < 15; i++ {
		lru.Add(i, i) //14 13 12 11 10 8 6 4 2 0
	}

	for i := 0; i < 15; i += 3 {
		_, exists := lru.Get(i)
		fmt.Printf("key %d exists %t\n", i, exists)
	}
}

练习-用go语言中的map和堆实现超时缓存

type HeapNode struct {
	value    int //对应到map里的key
	deadline int //到期时间戳，精确到秒
}

type Heap []*HeapNode

func (heap Heap) Len() int {
	return len(heap)
}
func (heap Heap) Less(i, j int) bool {
	return heap[i].deadline < heap[j].deadline
}
func (heap Heap) Swap(i, j int) {
	heap[i], heap[j] = heap[j], heap[i]
}
func (heap *Heap) Push(x interface{}) {
	node := x.(*HeapNode)
	*heap = append(*heap, node)
}
func (heap *Heap) Pop() (x interface{}) {
	n := len(*heap)
	last := (*heap)[n-1]
	//删除最后一个元素
	*heap = (*heap)[0 : n-1]
	return last //返回最后一个元素
}

type TimeoutCache struct {
	cache map[int]interface{}
	hp    Heap
}

func NewTimeoutCache(cap int) *TimeoutCache {
	tc := new(TimeoutCache)
	tc.cache = make(map[int]interface{}, cap)
	tc.hp = make(Heap, 0, 10)
	heap.Init(&tc.hp) //包装升级，从一个常规的slice升级为堆
	return tc
}

func (tc *TimeoutCache) Add(key int, value interface{}, life int) {
	//直接把key value放入map
	tc.cache[key] = value
	//计算出deadline，然后把key和deadline放入堆
	deadline := int(time.Now().Unix()) + life
	node := &HeapNode{value: key, deadline: deadline}
	heap.Push(&tc.hp, node)
}

func (tc TimeoutCache) Get(key int) (interface{}, bool) {
	value, exists := tc.cache[key]
	return value, exists
}

func (tc *TimeoutCache) taotai() {
	for {
		if tc.hp.Len() == 0 {
			time.Sleep(100 * time.Millisecond)
			continue
		}
		now := int(time.Now().Unix())
		top := tc.hp[0]
		if top.deadline < now {
			heap.Pop(&tc.hp)
			delete(tc.cache, top.value)
		} else { //堆顶还没有到期
			time.Sleep(100 * time.Millisecond)
		}
	}
}

func testTimeoutCache() {
	tc := NewTimeoutCache(10)
	go tc.taotai() //在子协程里面去执行，不影响主协程继续往后走

	tc.Add(1, "1", 1)
	tc.Add(2, "2", 3)
	tc.Add(3, "3", 4)

	time.Sleep(2 * time.Second)

	for _, key := range []int{1, 2, 3} {
		_, exists := tc.Get(key)
		fmt.Printf("key %d exists %t\n", key, exists) //1不存在，2 3还存在
	}
}