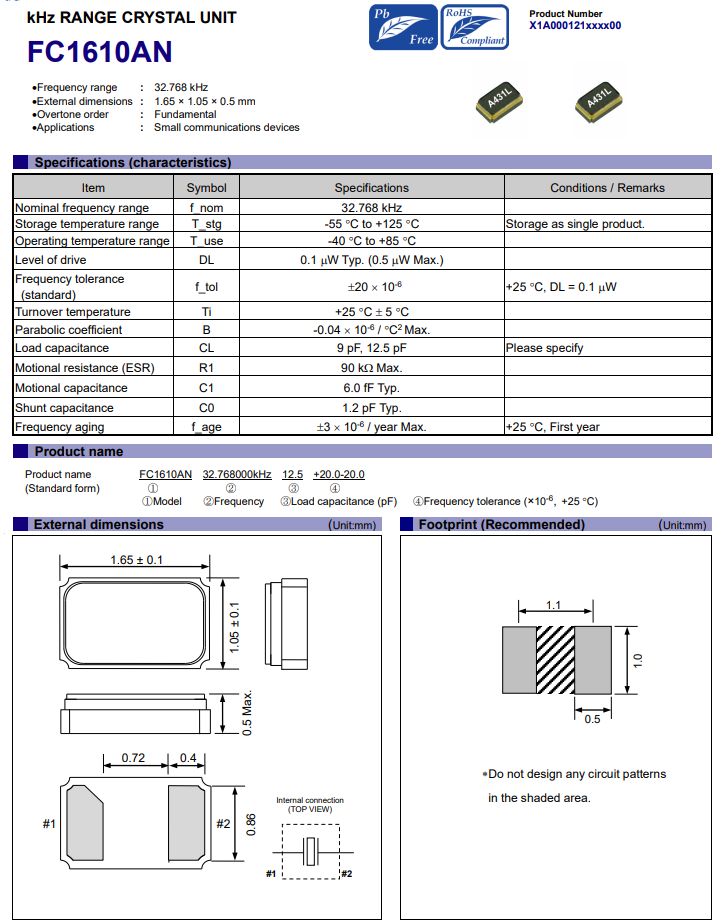
和为 s 的两个数字(easy)
- 题⽬描述:
- 解法⼀(暴⼒解法,会超时):
- 解法⼆(双指针 - 对撞指针):
- 算法思路:
- C++ 算法代码
- Java 算法代码:
题⽬链接: 剑指 Offer 57. 和为s的两个数字
题⽬描述:
输⼊⼀个递增排序的数组和⼀个数字 s ,在数组中查找两个数,使得它们的和正好是 s 。如果有多对数字的和等于 s ,则输出任意⼀对即可。
⽰例 1:
输⼊: nums = [2,7,11,15], target = 9
输出: [2,7] 或者 [7,2]
解法⼀(暴⼒解法,会超时):
算法思路:
两层 for 循环列出所有两个数字的组合,判断是否等于⽬标值。
算法流程:
两层 for 循环:
- 外层 for 循环依次枚举第⼀个数 a ;
- 内层 for 循环依次枚举第⼆个数 b ,让它与 a 匹配;
ps :这⾥有个魔⻤细节:我们挑选第⼆个数的时候,可以不从第⼀个数开始选,因为 a 前
⾯的数我们都已经在之前考虑过了;因此,我们可以从 a 往后的数开始列举。 - 然后将挑选的两个数相加,判断是否符合⽬标值。
算法代码:
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int n = nums.size();
for (int i = 0; i < n; i++) { // 第⼀层循环从前往后列举第⼀个数
for (int j = i + 1; j < n; j++) { // 第⼆层循环从 i 位置之后列举第⼆个数
if (nums[i] + nums[j] == target)// 两个数的和等于⽬标值,说明我们已经找到结果了
return {nums[i], nums[j]};
}
}
return {-1, -1};
}
};
解法⼆(双指针 - 对撞指针):
算法思路:
注意到本题是升序的数组,因此可以⽤「对撞指针」优化时间复杂度。
算法流程(附带算法分析,为什么可以使⽤对撞指针):
- 初始化 left , right 分别指向数组的左右两端(这⾥不是我们理解的指针,⽽是数组的下
标) - 当 left < right 的时候,⼀直循环
i. 当 nums[left] + nums[right] == target 时,说明找到结果,记录结果,并且返回;
ii. 当 nums[left] + nums[right] < target 时:
• 对于 nums[left] ⽽⾔,此时 nums[right] 相当于是 nums[left] 能碰到的最⼤值(别忘了,这⾥是升序数组哈~)。如果此时不符合要求,说明在这个数组⾥⾯,没有别的数符合 nums[left] 的要求了(最⼤的数都满⾜不了你,你已经没救了)。因此,我们可以⼤胆舍去这个数,让 left++ ,去⽐较下⼀组数据;
• 那对于 nums[right] ⽽⾔,由于此时两数之和是⼩于⽬标值的,nums[right]还可以选择⽐nums[left] ⼤的值继续努⼒达到⽬标值,因此 right 指针我们按兵不动;
iii. 当 nums[left] + nums[right] > target 时,同理我们可以舍去nums[right] (最⼩的数都满⾜不了你,你也没救了)。让 right-- ,继续⽐较下⼀组数据,⽽ left 指针不变(因为他还是可以去匹配⽐ nums[right] 更⼩的数的)。
C++ 算法代码
class Solution{
public:
vector<int> twoSum(vector<int>& nums, int target){
int left = 0, right = nums.size() - 1;
while(left < right){
int sum = nums[left] + nums[right];
if(sum > target) right--;
else if(sum < target) left++;
else return {nums[left], nums[right]};
}
// 照顾编译器
return {-4941, -1};
}
};
Java 算法代码:
class Solution{
public int[] twoSum(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left < right){
int sum = nums[left] + nums[right];
if(sum > target) right--;
else if(sum < target) left++;
else return new int[] {nums[left], nums[right]};
}
// 照顾编译器
return new int[]{0};
}
}