目录
坐标下降法
概念
坐标下降法的步骤
案例演示
数值优化算法面临的问题
凸优化问题与凸集
凸优化问题
性质
优点
凸集
性质
坐标下降法
概念
坐标下降法是一种非梯度优化算法。算法在每次迭代中,在当前点处沿一个坐标方向
进行一维搜索以求得一个函数的局部极小值。在整个过程中循环使用不同的坐标方向。
例如,要最小化函数f(x),即:min f (x), x = (x~1~, x~2~ ,…, x~n~ )
它的思想是按住其它的不动,只优化其中一个比如 x1 ,那就把多元函数求极值问题变成了
一元函数求极值问题,这样优化的难度就小了很多,紧接着我们把其它的按住不动,再优化
x2,一直到 xn ,完了之后再回来优化 x1,把所有的从 x1、 x2 到 xn 优化一遍,就好比梯
度下降迭代一次,计算的工作量小。
坐标下降法的步骤
-
初始化变量:选择初始变量的取值。
-
选择维度:按照一定的顺序或随机选择一个维度。
-
单变量优化:在选择的维度上,固定其他维度的变量,并对当前维度的变量进行优化,找到使目标函数最小(或最大)的值。
-
更新变量:将优化得到的当前维度上的变量值更新到整体变量中。
-
判断停止条件:检查是否满足停止条件,如目标函数的变化很小或达到最大迭代次数。
-
切换维度:如果未达到停止条件,则切换到下一个维度,重复步骤3到步骤5。
-
返回结果:返回最终优化得到的变量值作为最优解。
案例演示
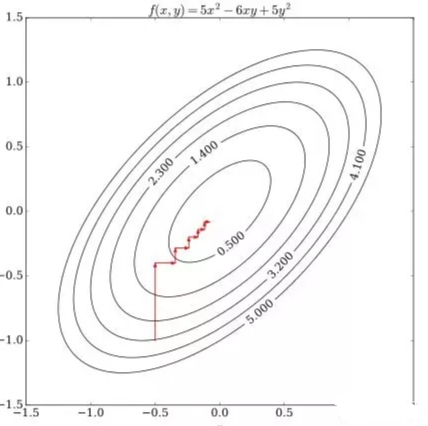
假设我们有目标函数f(x,y)=5x^2^-6xy+5y^2^,其等高线图如下所示,求(x, y)以使得目标
函数在该点的值最小。

图中红色十字标示的是起始点(-0.5, -1.0),此时f =3.25。现在我们固定x,将f
看成关于y的一元二次方程并求当f最小时y的值:

即,现在自变量的取值就更新成了(-0.5, -0.3), f = 0.8。
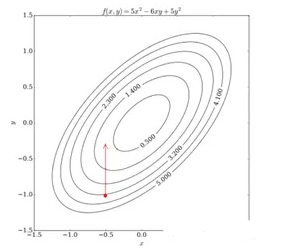
下一步,将新得到的y值固定,将f看成关于x的一元二次方程并求当函数最小时x的值。计算
过程与上一步相似,由于计算过于简单,我们直接绘制出经过多轮如上迭代后自变量(x,
y)的运动轨迹:
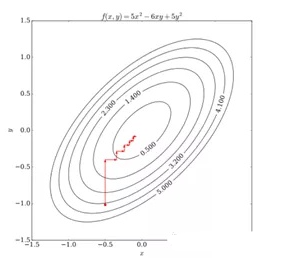
可见,随着(x, y )依次在相应坐标轴上的移动,目标函数逐渐接近其极小值点,直至
在某次迭代中函数得不到优化,即达到某一驻点后停止。
数值优化算法面临的问题
-
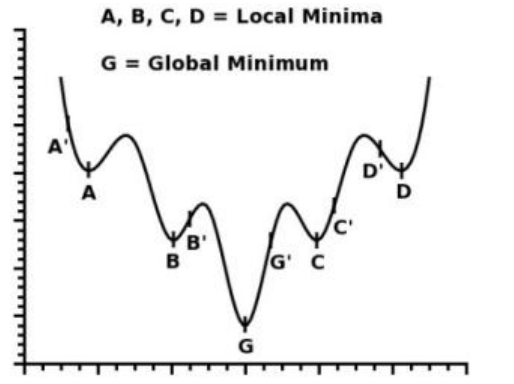
局部极值问题
要求全局最优解,要把所有极小值找出来,可能要不断的去设置不同的初始迭代点,
反复的求解让它收敛到不同的局部最小值,然后来比较谁最小来找到一个全局最小值
-
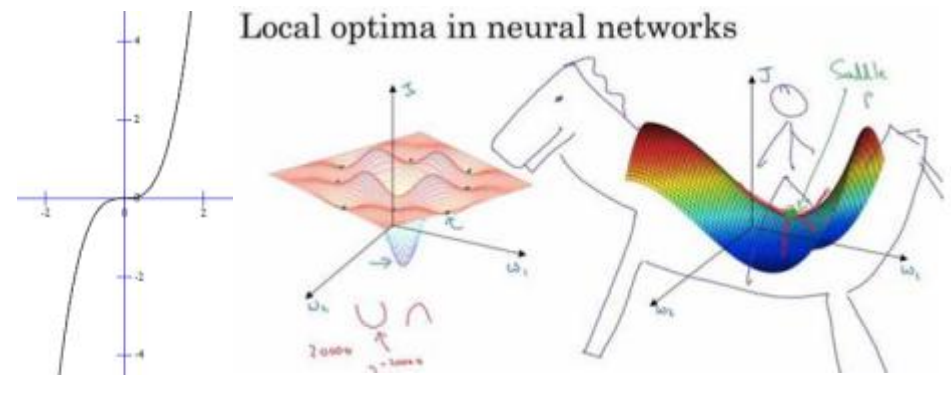
鞍点问题
一元函数 x^3^函数,在坐标为 0 处它是驻点,但是它连局部最小值点都不是,对应多元函
数来说,我们称之为鞍点(既不是极大值点也不是极小值点的临界点,叫做鞍点。)
凸优化问题与凸集
凸优化问题
前面我们说过数值优化面临两个问题,一个是局部极值问题,和鞍点问题,我们能不能避免
这两个问题呢?
只要我们对优化问题进行限定就可以,这类问题有两个限定条件
- 优化变量的可行域必须是凸集
- 优化函数必须是个凸函数
同时满足这两个限定条件的问题,叫做凸优化问题。一个凸优化问题的局部最优解就
是它的全局最优解。
性质
- 凸函数的定义域是凸集。凸集是指对于任意的两个点在集合内,连接这两个点的线段上的所有点也在集合内。
- 函数在定义域内的任意两点之间的连线上的函数值不大于这两个点上函数值的线段上的函数值。也就是说,凸函数的函数值不会出现“凹”的形状。
- 函数的二阶导数是非负的,即凸函数的二阶导数大于等于零。
优点
- 全局最优解:凸优化问题的局部最优解也是全局最优解,因此可以保证求解的结果是全局最优解。
- 唯一性:凸优化问题的解是唯一的,不存在多个不同的局部最优解。
- 算法可行性:凸优化问题可以通过多种有效的算法进行求解,如梯度下降法、牛顿法、内点法等。
凸集
对于一个点的集合C,有 x,y 它都是属于C里面的两个点,它们两点的连线中任何一点
也是属于集合C的。
例如,立方体是凸集,但是任何中空的或具有凹痕的例如月牙形都不是凸集。
性质
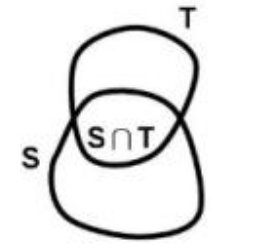
- 对于两个凸集的交集,它仍然是一个凸集。
- 对于一组凸集的并集,它仍然是一个凸集。
注意
- 凸集的交集也是凸集
- 凸集的并集不一定是凸集