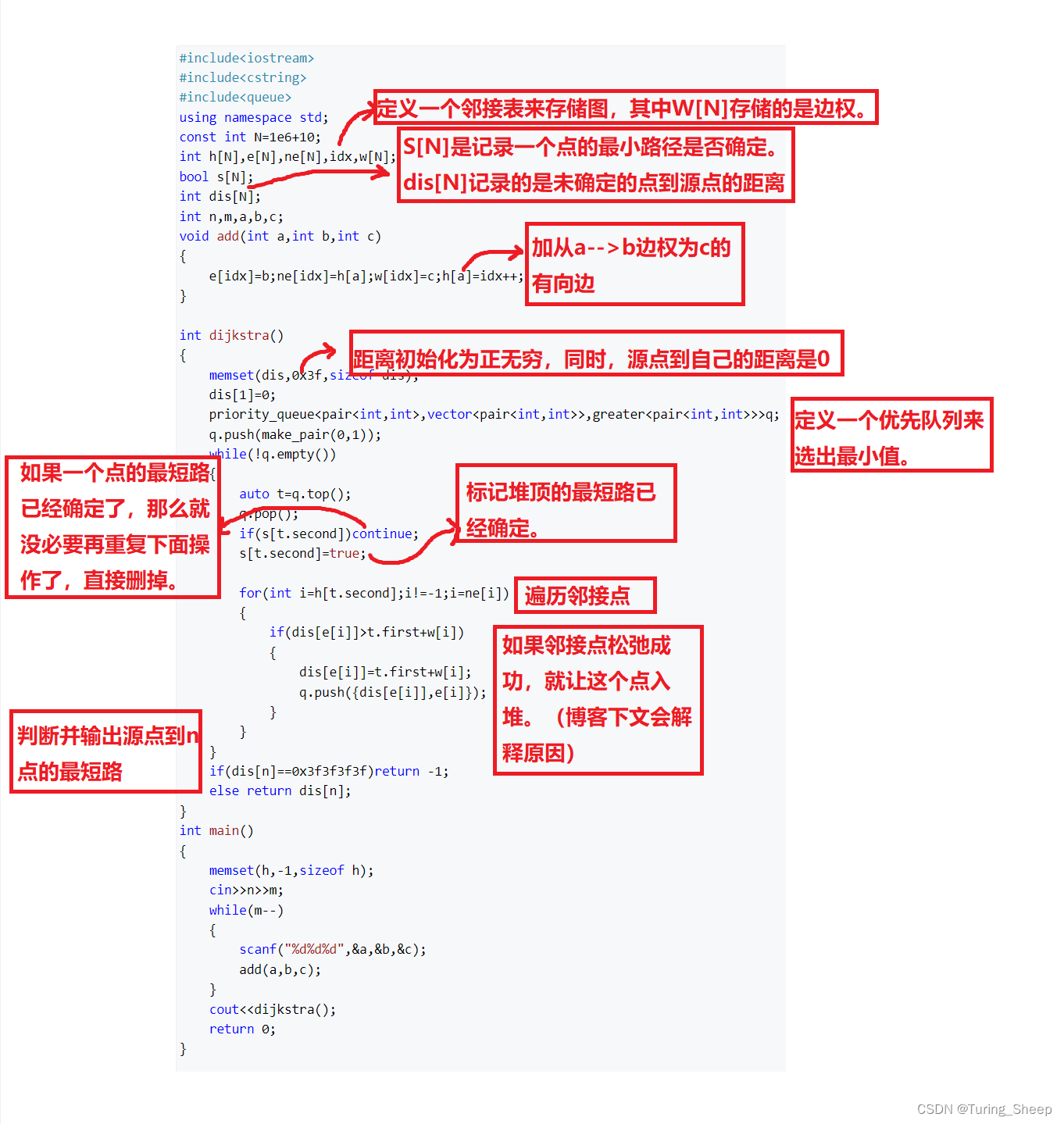
归并排序
归并的思路其实和二叉树,快排都有点像。归并希望左、右半区间有序。和快排不同,先分裂后排序,一半一半分,分到最后每个区间只剩一个1个数字,这个区间一定是有序的,因为只有一个数字,往回走,两个数排序一下,继续往回走,逐渐排序好后,回到初始的数组,这时候整个数组就已经有序了。这里我们用另一个数组来临时存储分出来的区间去排序,排好后再拷贝回去
要开辟一块新空间的话我们需要在另一个函数里开辟,如果在一个函数里会重复开辟。
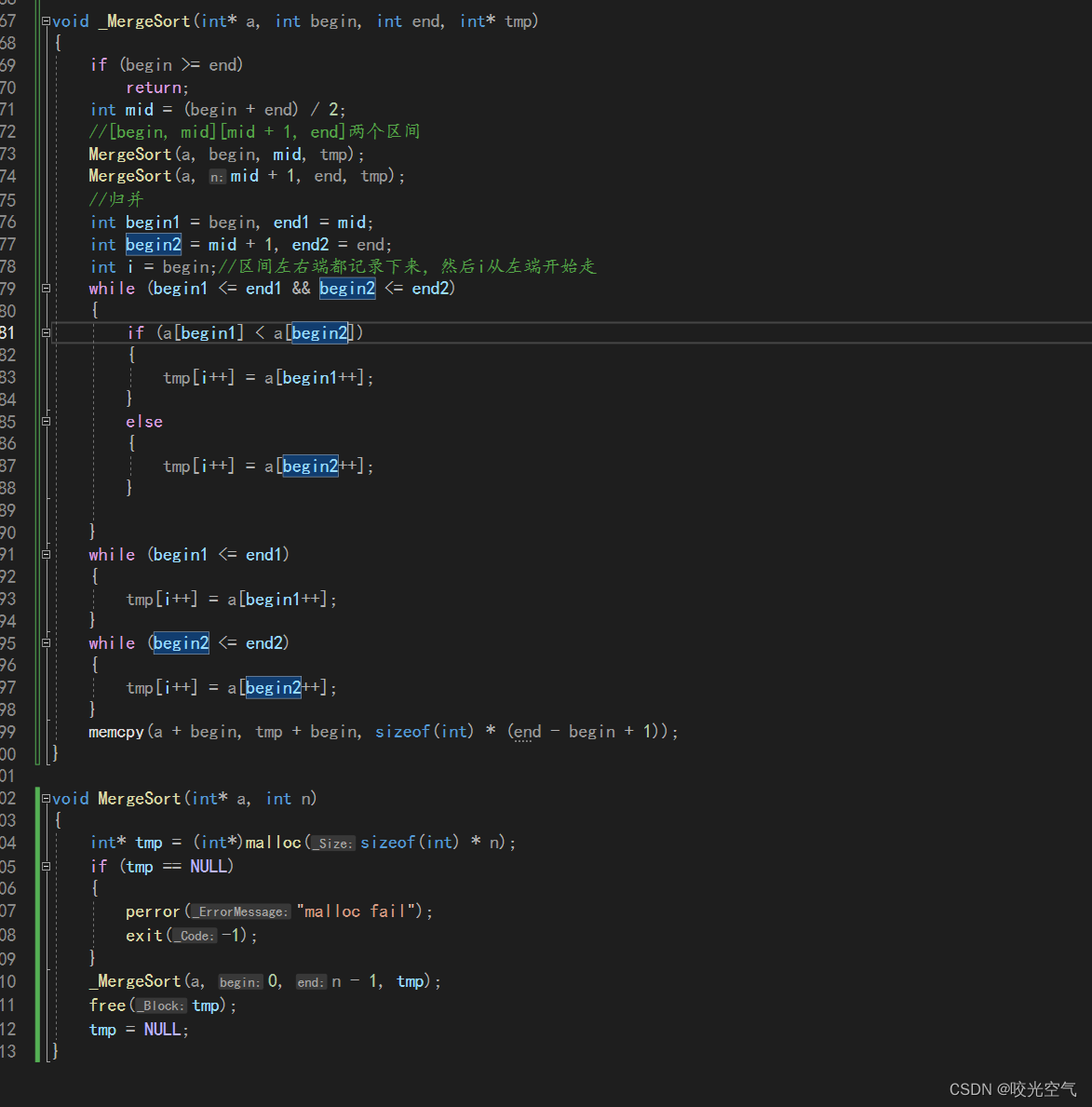
由于是先分裂,所以先递归出区间。用四个变量记录下来两个区间两端,进入while,这两个区间从头开始一个个比较,小的就放进tmp里,这样就有序了,当然这里会出现哪个区间先结束的情况,所以后面两个while就把没出完数据的那个区间都拿出来,然后拷贝到a里,这里用a + begin是因为不可能每次都从a的首元素处拷贝,所以加上begin,拷贝每个排好的区间。
可画递归展开图来理解代码。
归并的时间复杂度不难算,整个递归像一个二叉树,高度也就是logN。每一层的归并操作可以看出就是N,所以归并是个很正规的O(N * logN)。而空间复杂度也是经典的O(N)。因为额外开了tmp这个N个数据的空间。
而上一篇的快排虽然没有额外开辟空间,但它也是递归,递归层数也是logN。每一层快排没有额外的操作,是O(1),所以它的空间复杂度是O(logN).
归并的空间复杂度刚才算了tmp,不过递归层数也要计入,所以应该是N + logN,但N很大时,logN很小啊,可以忽略不计。所以还是O(N)
非递归归并
归并的非递归需要用到链表,不过我们这里可以不用这样。和快排不一样,归并并不一定要按照递归做非递归。归并的分区间是确定,对半分,分到每个区间一个数。所以我们重点在于控制单个区间的大小。定义一个range变量控制区间,这里其实和斐波那契数列改非递归思路一样,斐波那契数列非递归就是先写出头两个数字,然后在循环里加,得到下一个数字,然后头两个数字也往后移一下。归并的非递归则是先把数组里所有的数分成若干个两个数的单位,两个数之间排序,然后让range * 2,四个数之间再排序,然后再次 * 2,变成8个数之间排序等等。虽然这个思路很不错,但是实际写代码时细节问题却有很多。这个方法也需要一个tmp。
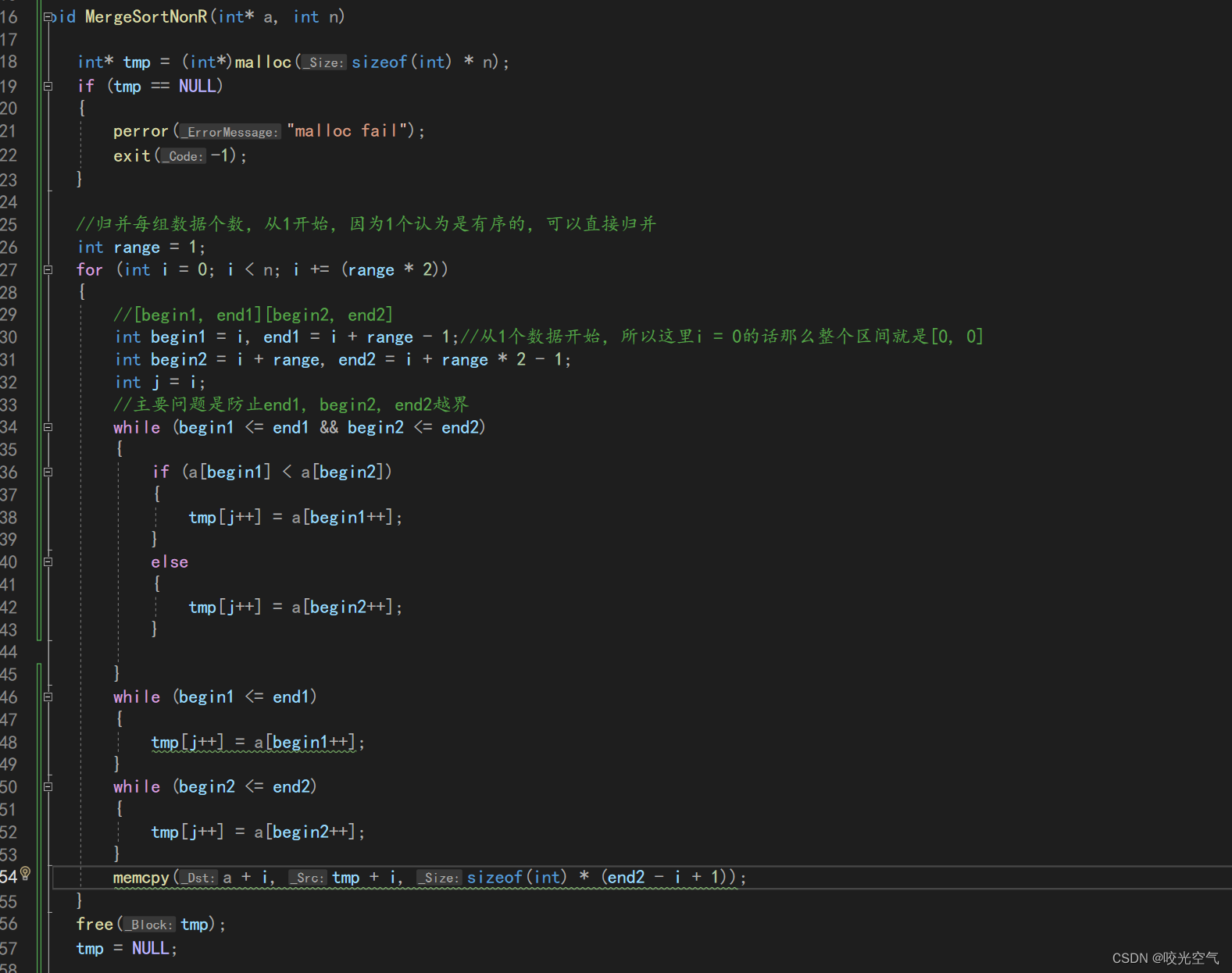
进入for循环后我们还是和之前一样的归并,所以直接复制过来,改改变量,而memcpy可以在整个循环结束后再拷贝,也可以一次次地拷贝,只不过在内部拷贝会更容易控制些。range * 2继续下一个循环。
现在只是完成了一层循环,range还要*2,继续扩大范围去排序
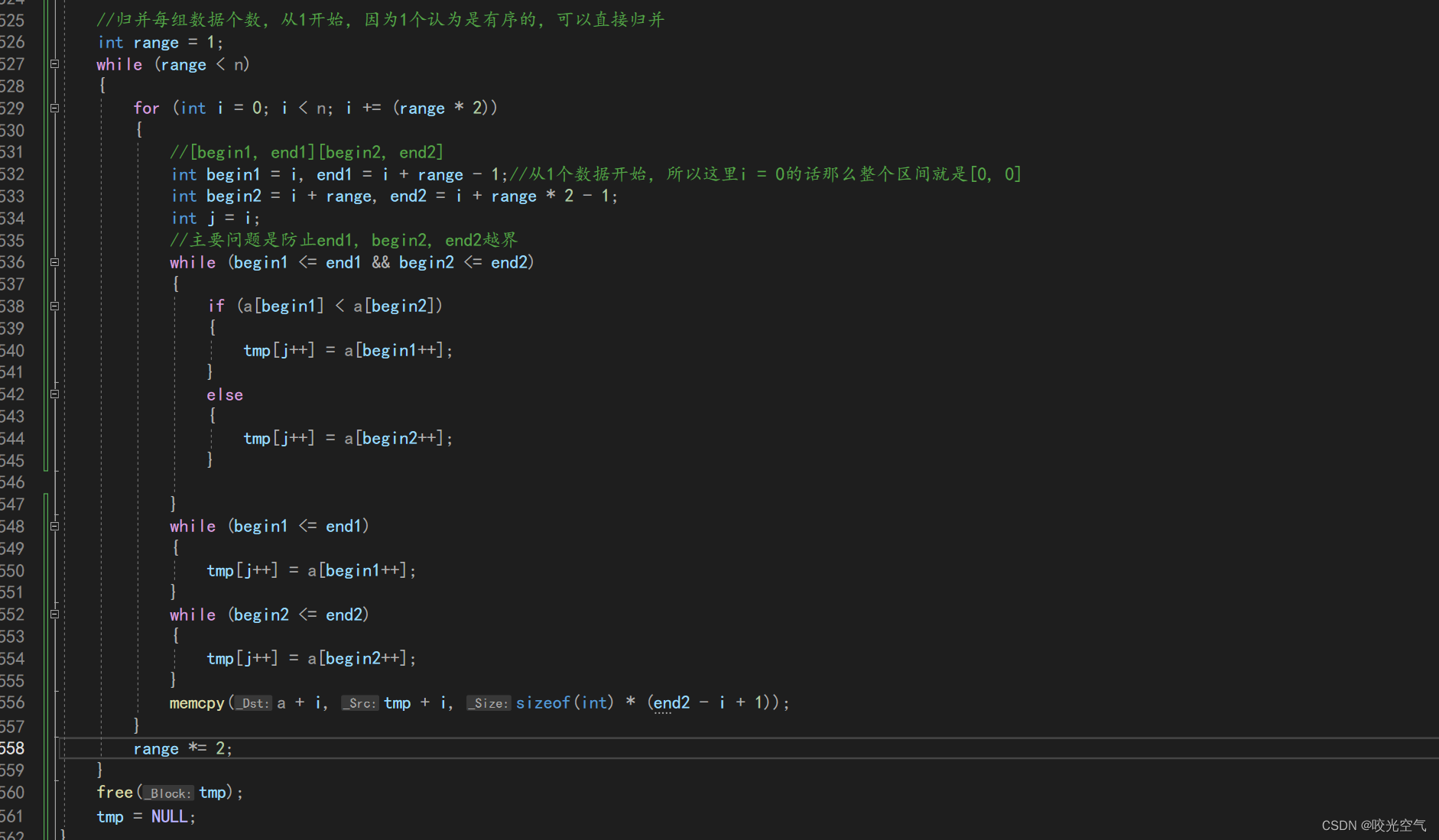
外面再套上一个while循环。不过这个代码还没有结束。

按照这个例子,程序自然可以排序出来,但这里的问题正如对半分区间一样,并不是每个数组都可以完全对半分,总会有一些数字和数组外的数据组成了一个区间,所以程序就出来问题,比如排序10个数程序就错了,只要数据总数不是2的幂次方个就有问题。现在这个程序中间归并的过程没有问题,问题应当出现在拷贝或者开始归并之前是否缺少了判断。
为了观察越界问题,在确定好begin和end参数后打印出来看看。1-10这10个数的处理结果

那么如何规避越界问题?
从代码角度看,end1, begin2,end2都容易越界,begin1 = i,所以不太会越界。图中也是,三个都出现越界了。现在的越界情况可以分为三种。如果end1,越界了,那么begin2和end2肯定都越界了,比如图中[8, 11]那一行;end1没越界,begin2越界了,end2也就越界了,比如图中[8, 9]那一行;end2自己越界了,比如图中[0, 7]那一行 ,所以要针对这三个情况来处理。
以10个数为例
end1越界
发生越界了,那么修正一下区间是不是就可行了,end1如果 >= n ,那么就改成n - 1,这样begin2 ,end2也就要被改成n和n - 1了,那么begin2这个区间就一定不会进入了,只排begin1这个区间。这时候2这个区间就是[10, 9],实际上已经越界,不过下面的归并算法并不会让他进入循环,所以只是一个数字罢了,而end1是9,这样就可以避免越界问题的发生,数组所有元素也都进入了排序,这种解决办法对于后面的拷贝没有多少影响,全部排序完再拷贝(外部拷贝)或者排序一次拷贝一次(内部拷贝)都可。
还有另外一种方法,如果遇到越界了,我们就break直接退出,不排序了,这样的结果也不必担心,最终都会排序成功,但是break有一个问题,选择break的话外部拷贝就难以控制了,因为里面存在越界的时候,外部拷贝有可能就把随机值给拷贝回去了。
这里我们采用break的办法,使用修正区间的话后面两个越界问题的处理也会有相应的变化,下面再写。
begin2越界
这个比较简单,第二个区间越界了那就不归并了。直接break。

end2越界
end2越界,那我们直接修正即可。

这样最终的代码就是这样
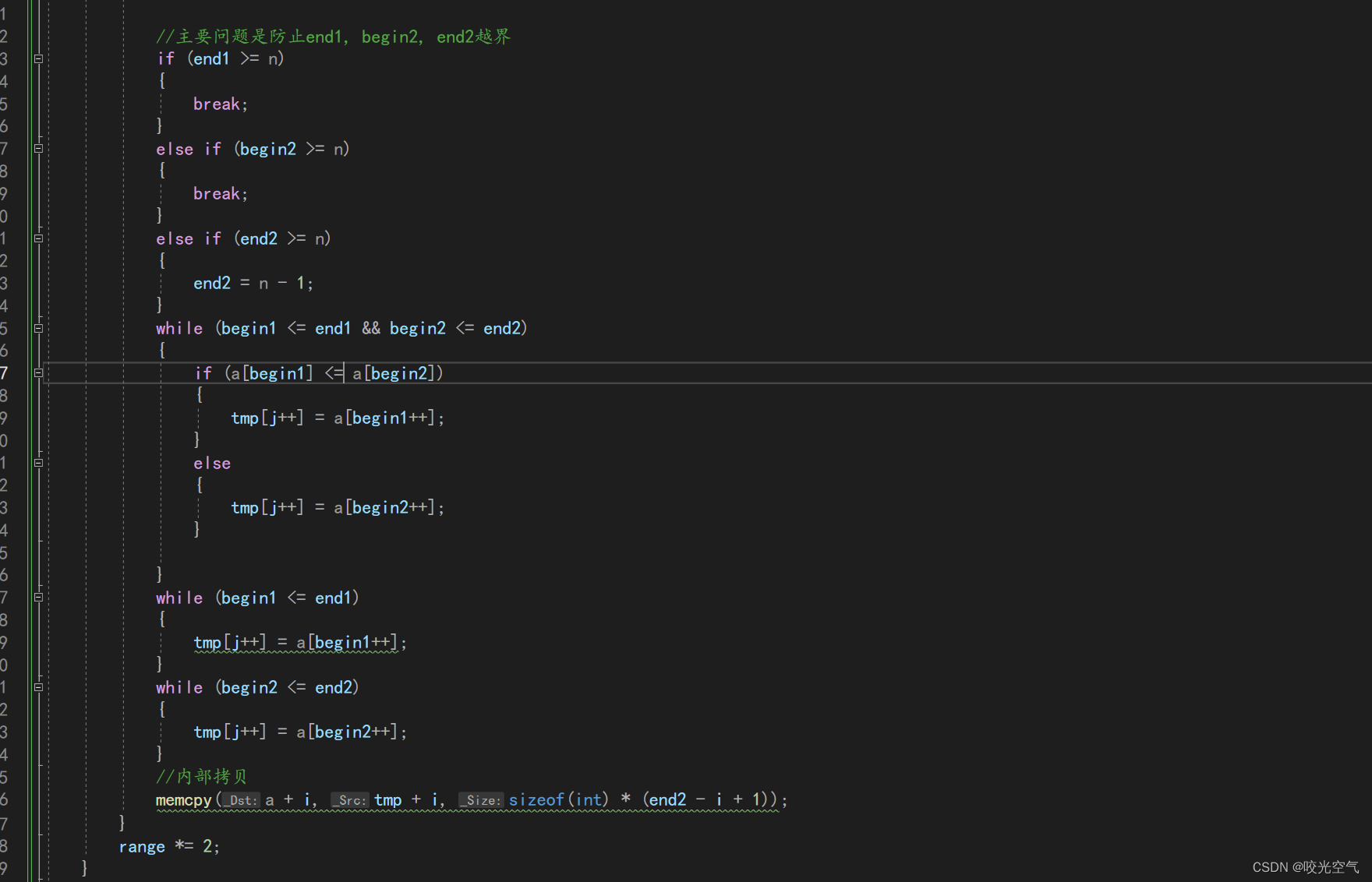
那么如果end1越界 用修正方法,end2越界也还是用修正,begin2越界的话就不需要归并,那么修正一下,让这个区间进不去循环即可。
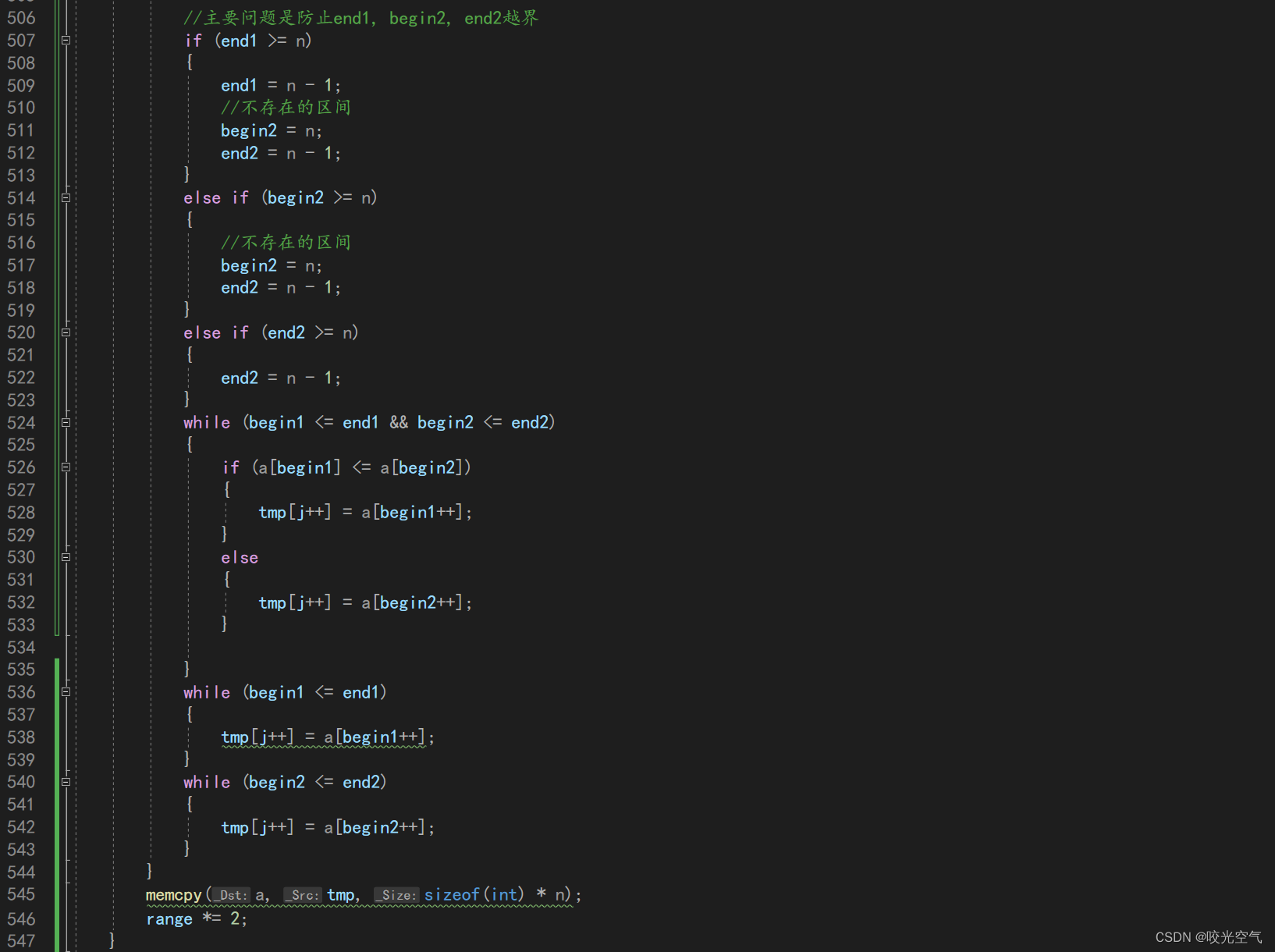
排序稳定性
这里会联合之前的两个复杂度,总结每个排序.
稳定性是指原始数组里同样的值的前后顺序在排序后的顺序是否正确。排序前什么顺序,排序后相对顺序仍然不变,那就是稳定,反之不稳定。

插入排序
直接插入排序:时O(N^2), 空O(1)。它稳定吗?

直接插入排序稳定啊,插入算法里如果后面的值小于前面的,那就互换,如果相等那就跳过,继续往后走,所以相同值的相对顺序是不变的
希尔排序:时O(N^1.3), 空O(1)。它稳定吗?
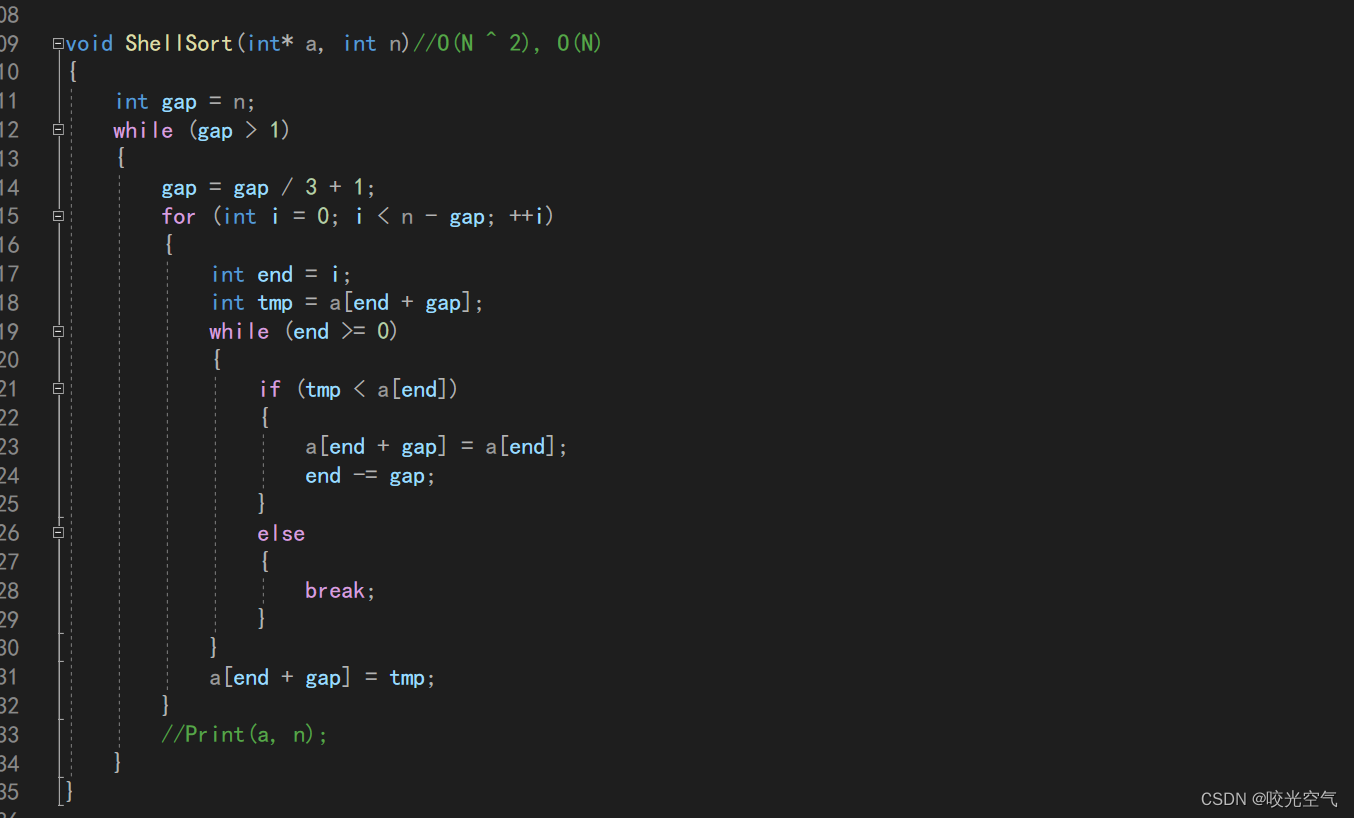
希尔顺序不稳定。 因为预排序时相同的数据就不保证顺序还是和之前一样了,因为会分到不同的组。
选择排序
选择排序:时O(N^2), 空O(1)。它稳定吗?
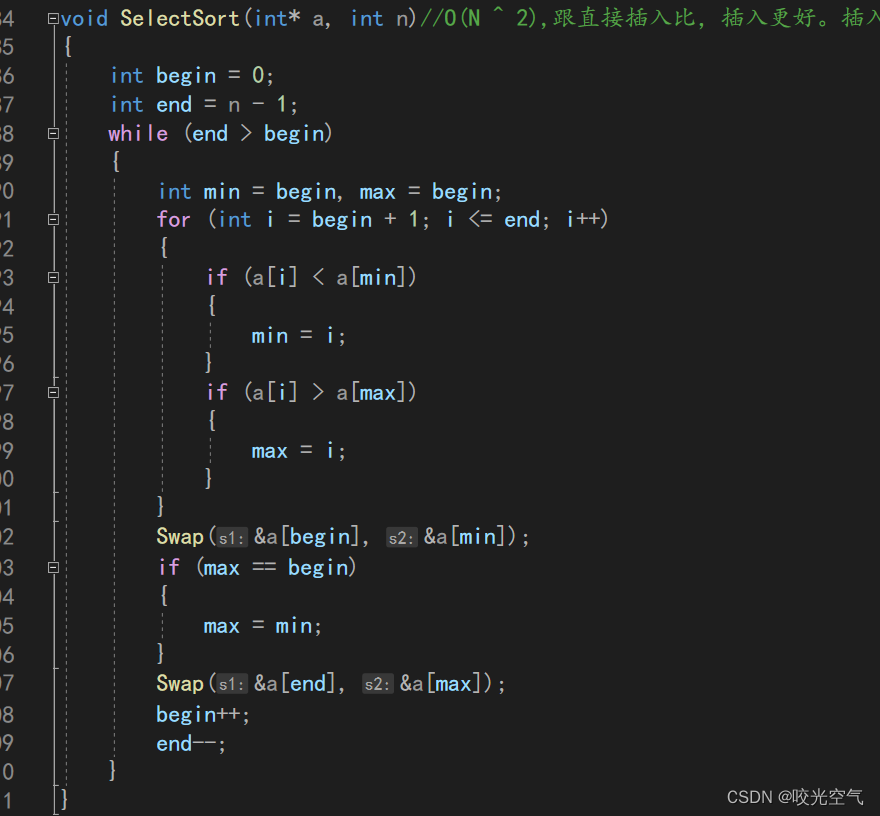
选择排序不稳定。举一个特例,总共4个数7744.代入进函数就会发现两个4和两个7的顺序无法保证,所以选择排序其实是不稳定的。
堆排序:时O(N*logN), 空O(1), 它稳定吗?
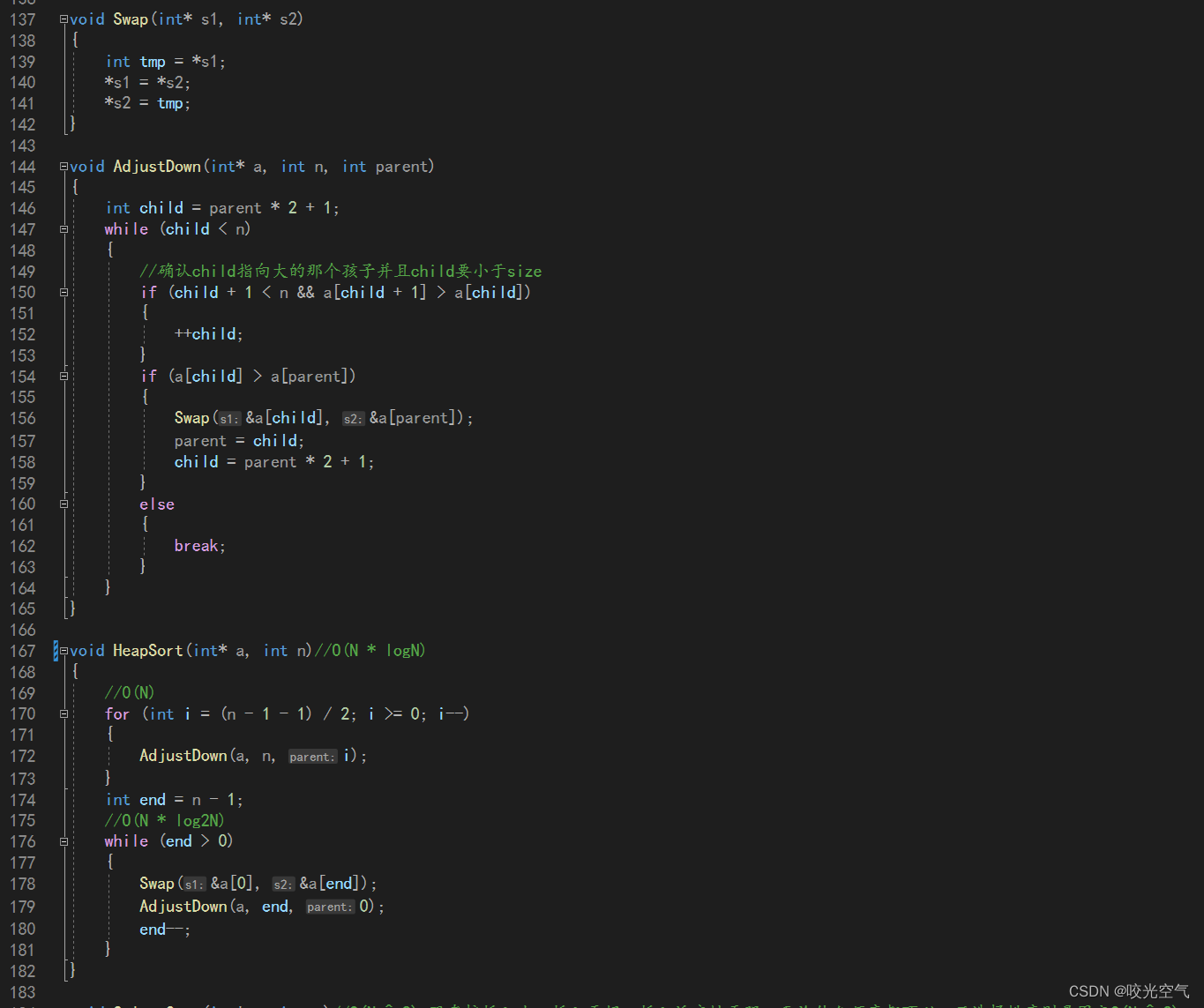
堆排序不稳定啊,即使放入堆的时候顺序对,但是堆排需要向下调整,这时候就无法保证了
交换排序
冒泡排序:时O(N^2),空O(1),它稳定吗?
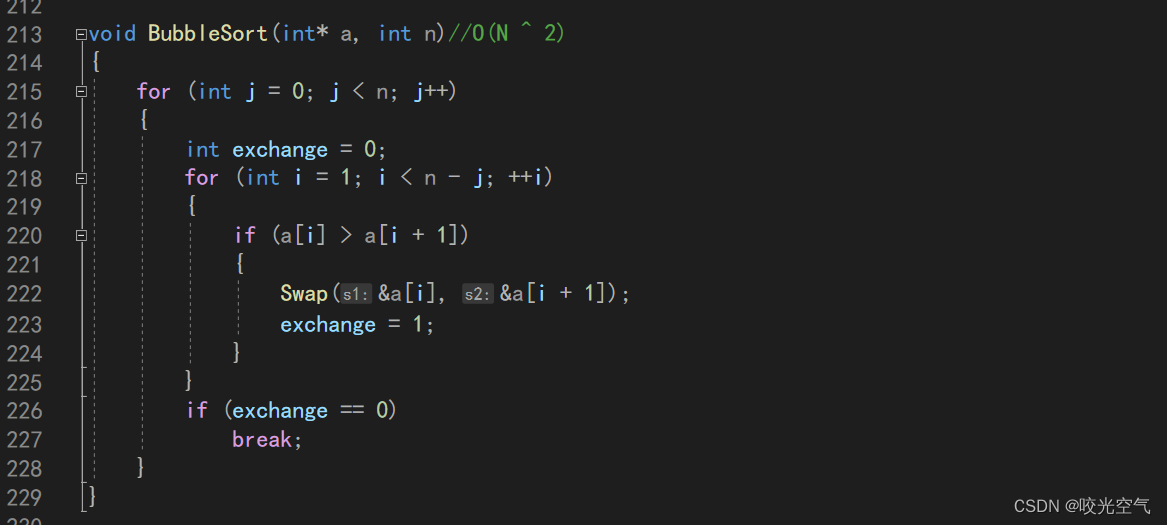
冒泡排序稳定。这个好理解。可以看到,两个数相等的时候就不换,所以能够稳定。
快排:时O(N*logN), 空O(logN),它稳定吗?
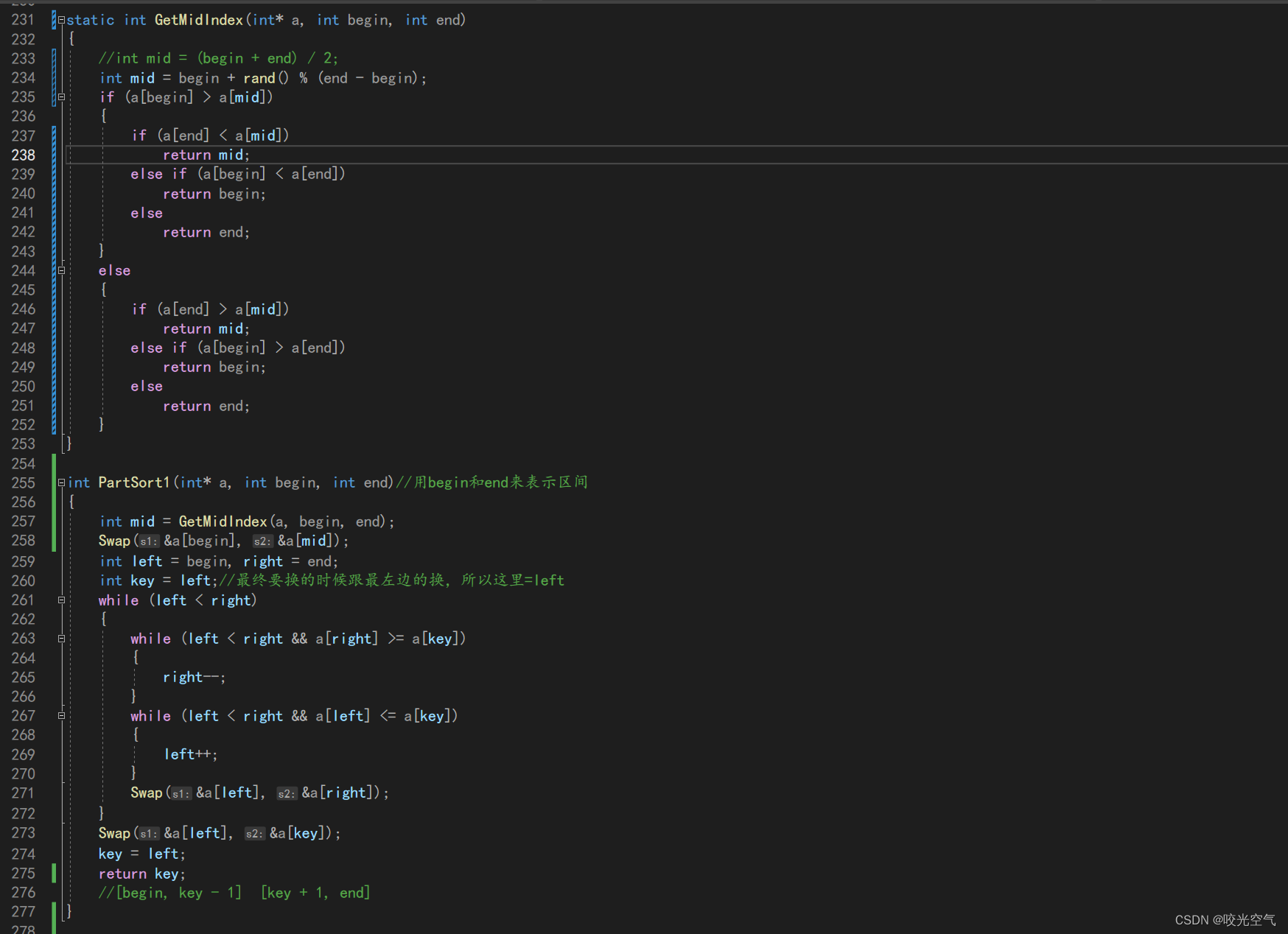
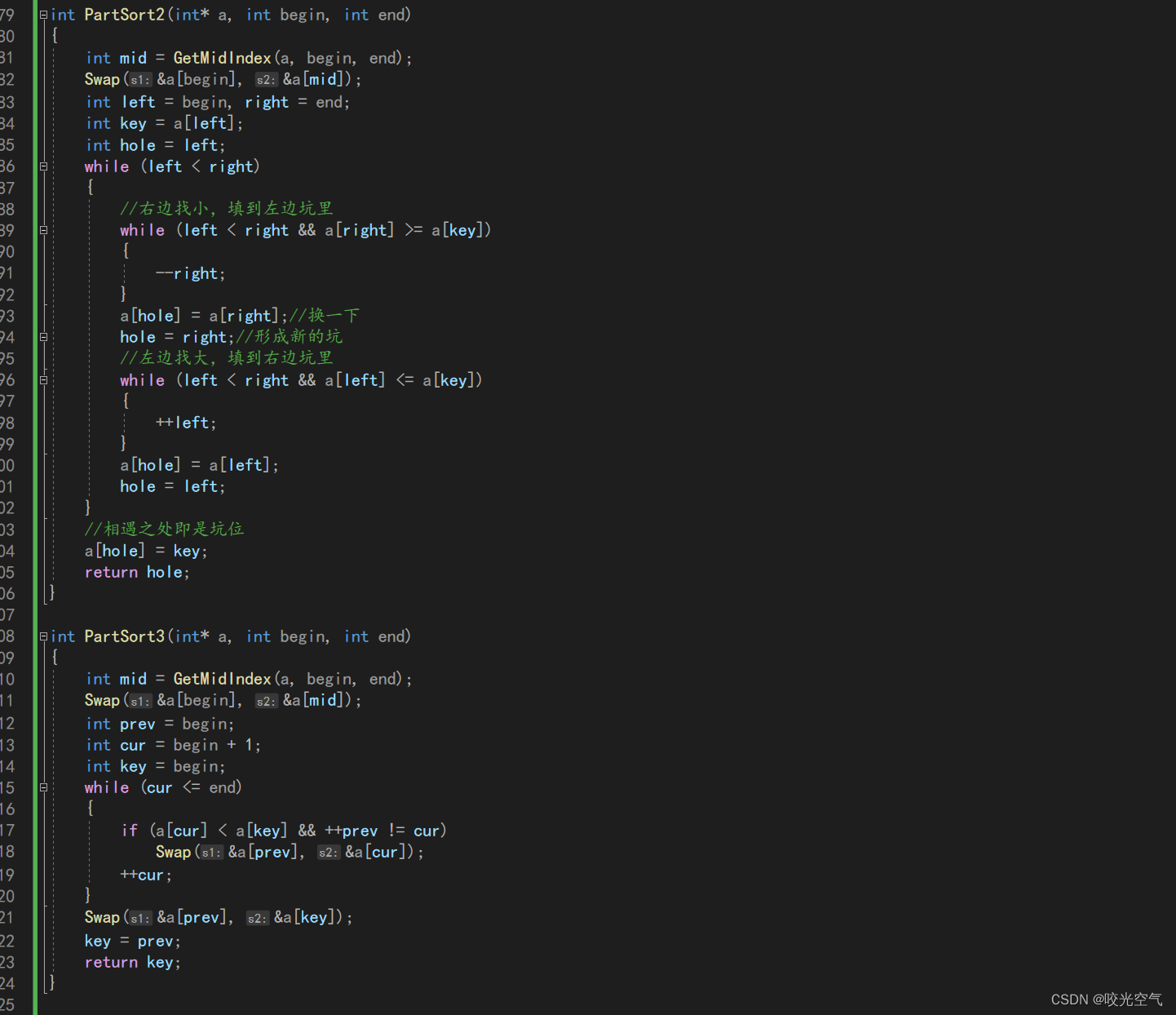

快排不稳定。快排中它不要求相对顺序,它需要一个个比较,然后交换,停下后再和key交换,所以无法保证稳定。
归并排序:时O(N*logN), 空O(N),它稳定吗?
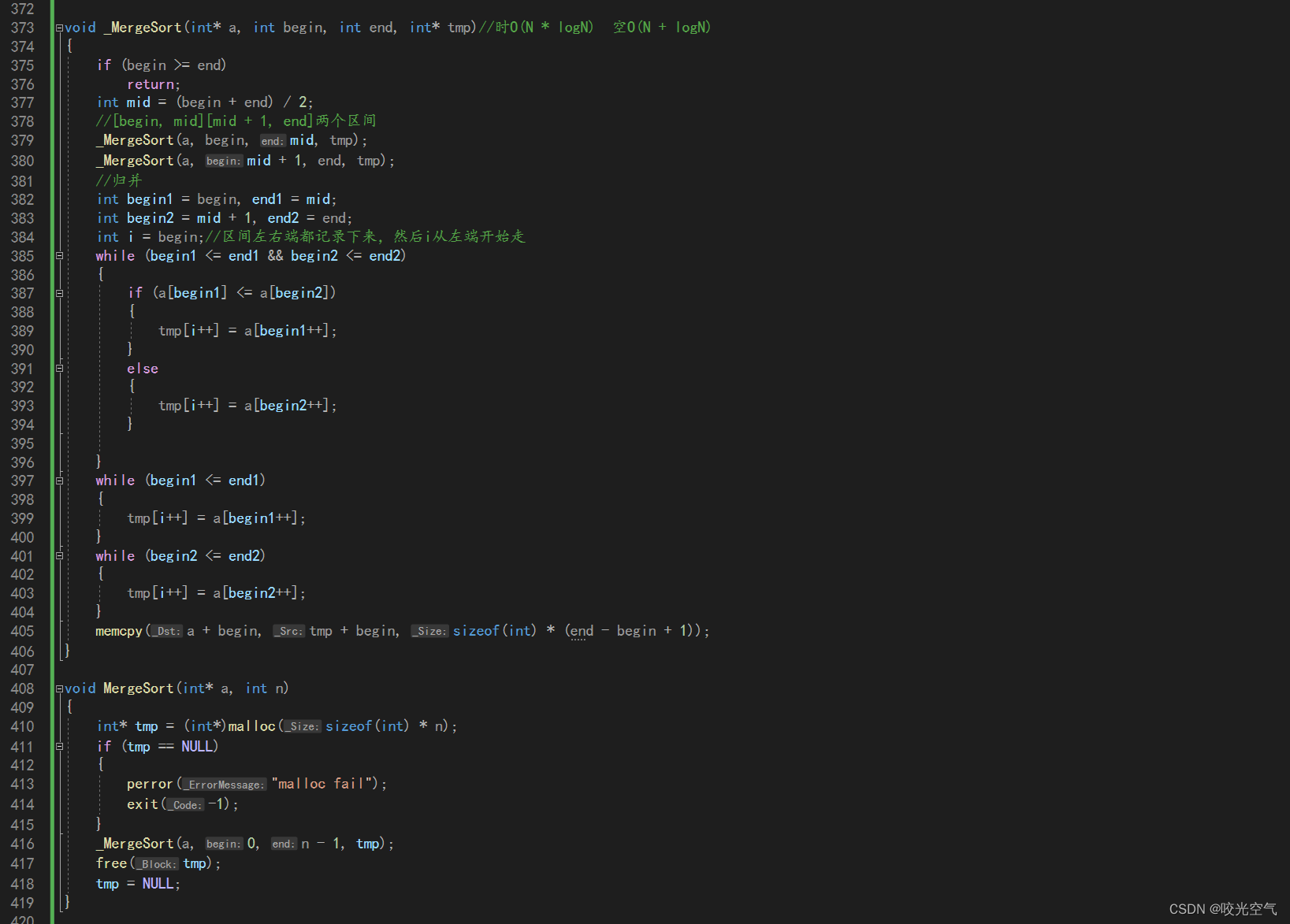
归并排序稳定。归并排序是在tmp中相当于取小的尾插进tmp中,那么相对顺序也就可以保证。
当然稳定的排序也可以不稳定,比如归并排序中a[begin1] < a[begin2]就不稳定了。
看一个特殊的例子
对于现在我们写的快排,如果数组里全是同一个数字,那么这个程序就很难受
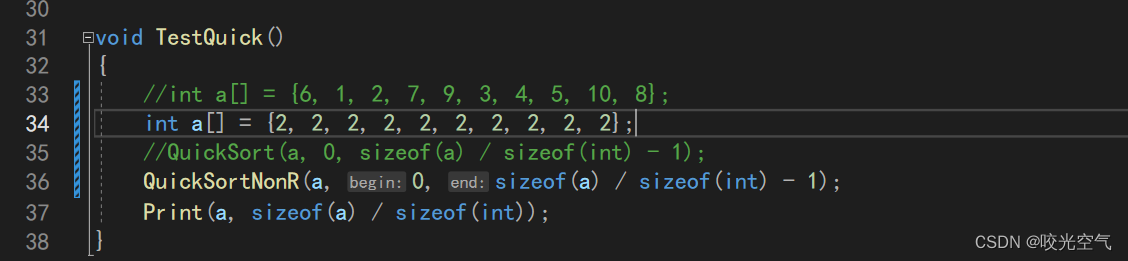
这个问题的描述就是对于大量的重复数据,在key是这个重复数据时,存在性能下降的问题。
以往快排的结果是key在中间,左边是 <= key的, 右边是 >= key的,这是两路划分。针对重复数据这个问题,有三路划分的办法,三路划分即为把整个数据分成三部分,小于key的,等于key的,大于key的,如果没有和key相等的,其实就和二路划分一样,有就放到等于key这个区间里,这块区间一直不要动,只递归大于和小于key的区间。
建三个变量,left,right,cur。

这是第一种情况,互换后cur指向第三个数据,left指向第二个数据


最后一个情况cur之所以是因为,right原本指向的数据并不确定是否大于小于key,所以还需要原地判断。
继续往后走,当cur大于right时整个过程就结束了。这时候整个区间就出来结果了。145 66666 87.三个区间。
代码实现

把找key的代码放到快排函数里。
这里还有一个问题,三数取中算法有点问题。
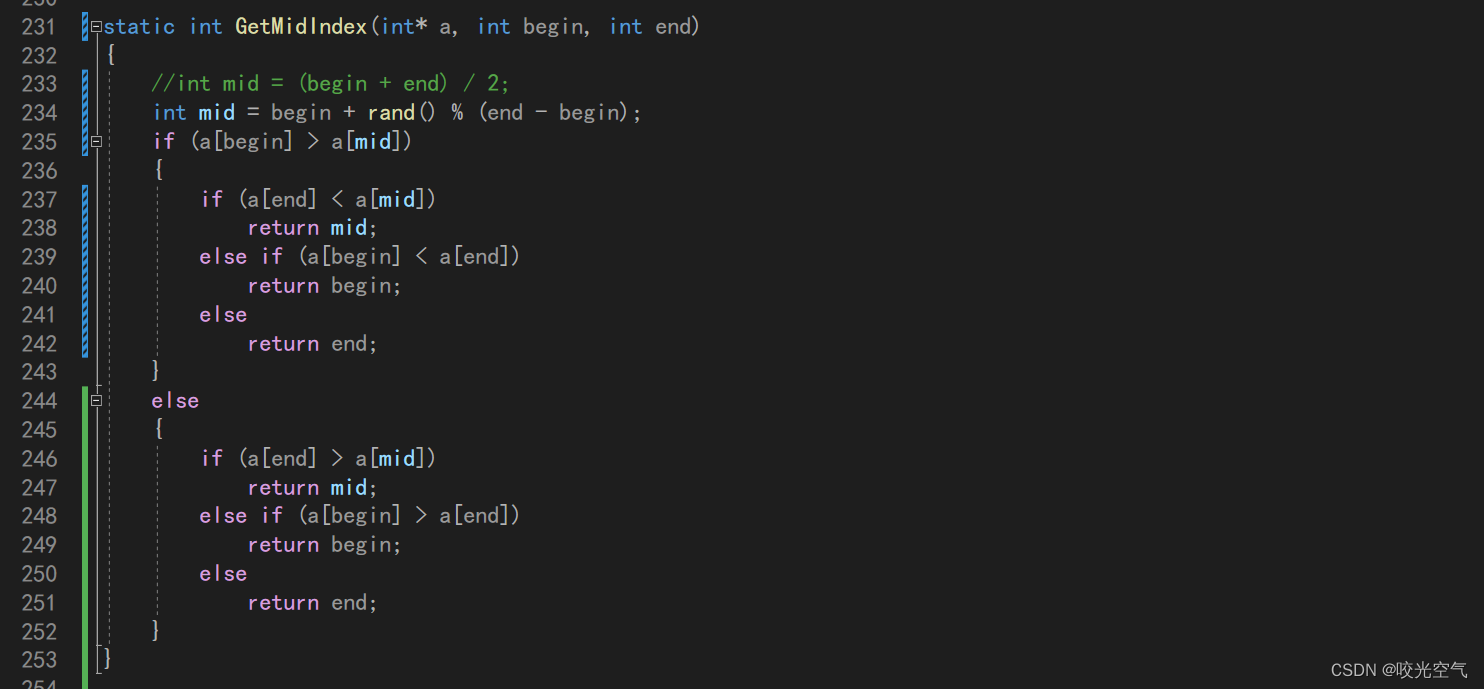
在力扣上会有很多特殊用例,如果按照之前的三数取中办法可能也会受到影响选到很小或很大的数字,所以改成随机数取key
结束。