一、普通dijkstra算法的缺陷

作者在这里建议，不太懂dijkstra算法的同学可以去看看作者对该算法的详细讲解以及通俗证明，这样大家就能够体会到原算法的缺陷。
传送门：第十六章 Dijkstra算法的讲解以及证明（与众不同的通俗证明）

1、选出最小距离的过程：

     int t=-1;
     for(int j=1;j<=n;j++)
     {
         if(!s[j]&&(t==-1||dis[j]<dis[t]))t=j;
     }

我们的dijkstra算法会选出所有松弛后所得距离的最小值。而我们之前的代码是遍历所有点来确定的，时间复杂度是O(N)。但是我们知道，我们在一堆数中选出一个最小值，只需要使用我们之前学过的数据结构：堆。假设我们插入一个最小值，那么堆选出这个值的时间复杂度是O(logN)。那么形成一个堆的话，即插入n个数的时间复杂度，并不是nlogn，而是O(N)
推导如下：
在这里插入图片描述

数据结构堆就是STL中的优先队列：priority_queue

2、松弛所有点的过程：

        
        for(int j=1;j<=n;j++)
        {
            dis[j]=min(dis[j],g[t][j]+dis[t]);
        }

通过我们第十五章对dijkstra算法的证明，我们发现，每次松弛过程得到有效更新的点，都是我们中间点的邻接点。也就是说，我们只需要去松弛该点的邻接点即可，不用去松弛所有点。因此，我们只需要去松弛该点的邻接点。那么这个时候，我们用邻接表就会便于我们去访问了。因为邻接表中将一个点的所有邻接点都记录在了链表中。我们只需要遍历对应点的链表即可。

二、如何优化

1、代码模板

（1）问题：

在这里插入图片描述

（2）模板：

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N=1e6+10;
int h[N],e[N],ne[N],idx,w[N];
bool s[N];
int dis[N];
int n,m,a,b,c;
void add(int a,int b,int c)
{
    e[idx]=b;ne[idx]=h[a];w[idx]=c;h[a]=idx++;
}
int dijkstra()
{
    memset(dis,0x3f,sizeof dis);
    dis[1]=0;
    priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>q;
    q.push(make_pair(0,1));
    while(!q.empty())
    {
        auto t=q.top();
        q.pop();
        if(s[t.second])continue;
        s[t.second]=true;

        for(int i=h[t.second];i!=-1;i=ne[i])
        {
            if(dis[e[i]]>t.first+w[i])
            {
                dis[e[i]]=t.first+w[i];
                q.push({dis[e[i]],e[i]});
            }
        }
    }
    if(dis[n]==0x3f3f3f3f)return -1;
    else return dis[n];
}
int main()
{
    memset(h,-1,sizeof h);
    cin>>n>>m;
    while(m--)
    {
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    cout<<dijkstra();
    return 0;
}

2、详细解读

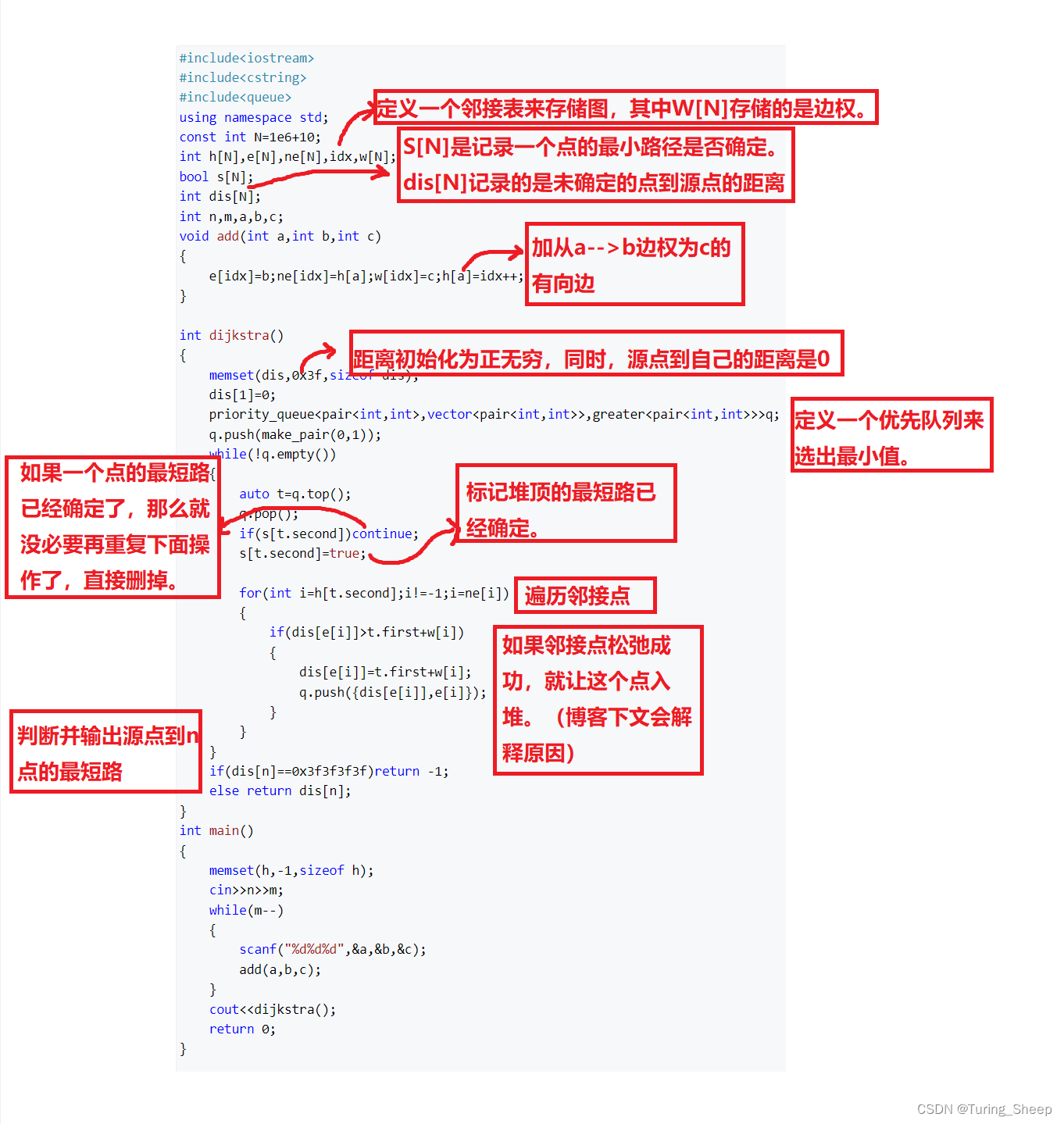
在这里插入图片描述

三、优化分析

1、使用条件：

我们这道题中的图是稀疏图，所以我们可以使用邻接表，从而优化这个代码。但是要是稠密图的话，我们可能还是需要用邻接矩阵来存储，这样的话一般使用的是朴素的dijkstra算法。

2、常见问题：

（1）什么样的路径才能进优先队列

只有一个点得到有效更新的时候，我们才会让这个点进堆。我们一开始是正无穷，那么源点的邻接点一定会得到有效的更新，那么我们让这些点进堆。那么第二次我们遍历的邻接点中，如果还包含上一次松弛后的点，而恰好本次也没有更新成功，那么我们让这个点进堆的话，堆中就会出现两个一样的数据。这样就造成了重复。而我们让不更新的点进堆，并不是说这个点已经确定了，而是说这个点的状态在之前的更新过程中已经进堆了。

所以，我们只让那些松弛成功的点进堆。

（2）重边的处理

我们的邻接矩阵存储图的时候，会通过min函数存储重边中的最小边。但是我们的邻接表会存储所有重边。这其实是没关系的。比如我们a,b点内存储了3，1，2。三个长度的边。一开始可能会让3+x这个距离进堆，但是我们当再次遍历到1这个边，松弛成功后我们就会让1+x进堆。而1+x存在后，3+x就不会成堆顶，所以就不会对结果产生影响。那么当我们的1+x出堆后，说明这个点的最短路已经确定了。那么我们直接标记一下，所以当1+x删除后，轮到3+x出堆的时候，由于我们已经标记了。所以通过continue就可以直接删除3+x这个数据。而后续的2+x也会在轮到它出堆的时候，删除掉。