【paper】 Effective Blending of Two and Three-way Interactions for Modeling Multi-relational Data

【简介】 本文是法国 Antoine Bordes 团队发表在 ECML-PKDD 2014 上的工作，提出了 TATEC（Two and Three-way Embeddings Combination）主要思想是混合二元和三元模型，分别训练然后进行联合微调。

motivation

文章提出，之前的模型，要么太复杂导致过拟合，要么太简单导致 capacity 不够，因此本文提出折中的办法，结合 high-capacity模型（三元交互）和 简单模型（二元交互），分别预训练并进行联合微调。

3-way interaction 的 large capacity 会导致过拟合，解决方法有二，一是加正则项，但会削弱模型表现力；而是使用二元交互，对于三元组 (h,r,t)(h,r,t)，使用其二元交互项 (h,t)(h,t)、(t,l)(t,l) 和 (h,l)(h,l)。文中说 TransE 属于二元交互模型。但是基于二元交互的方法是有限的，不能表示实体间所有类型的关系。

因此本文提出了一个 latent factor model，结合了 well-controlled 2-way 交互和 high-capacity 3-way 交互。这是一个之前模型的泛化，并且不像 LFM 和 NTN，在二元和三元交互的 component 之间不进行参数共享。

模型

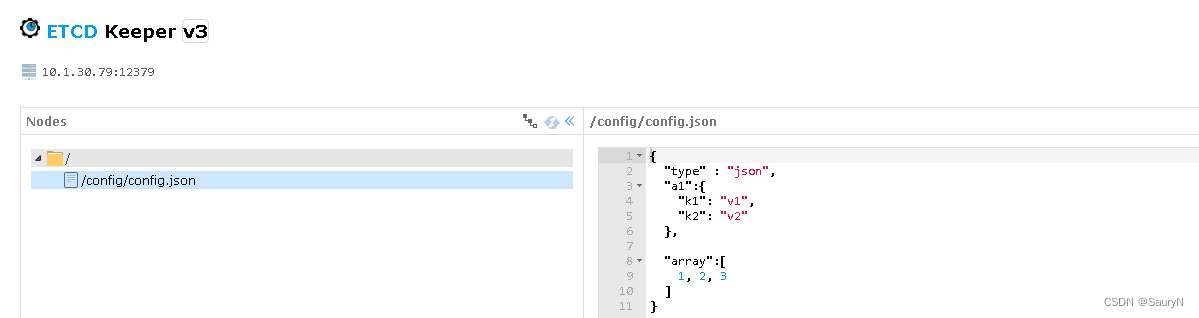
三元组的整体打分函数为二元交互和三元交互两部分得分之和：

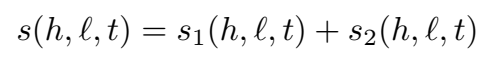
二元交互

bigram 二元交互项：

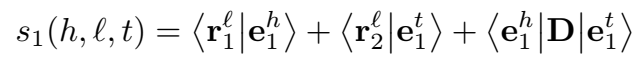
其中，rl1r1l 和 rl2r2l 是与关系有关的用于头尾实体投影的两个向量，DD 是对角矩阵，<.|.><.|.> 是普通的点积。

TransE 可以被视为 rl1=−rl2r1l=−r2l 的特殊情况。

三元交互

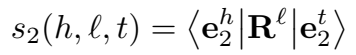
其中，RlRl 是维度为 (d1,d2)(d1,d2) 的矩阵。

文中提到，三元交互模型基本上可以表示实体间的任何交互。这里文章强调了两点，一是二元和三元两部分间没有参数共享，而是没有用于正则化的全局约束项。

训练

负采样：

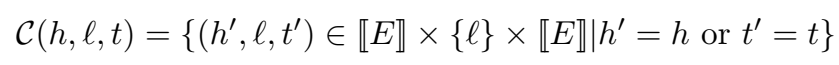
loss function：

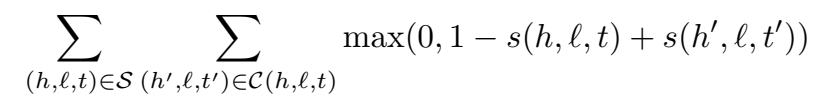
前面提到说没有正则化，但是训的时候也加了 L2 范数约束。

训练时首先分别训练 bigram term 和 trigram term，然后用学到的权重初始化 full score 并进行微调，用 SGD 训练 full model。

后面用了整整一章介绍模型的 motivation，并类比推荐系统协同过滤中“用户-物品”矩阵的各项。

实验

链接预测的结果：

---

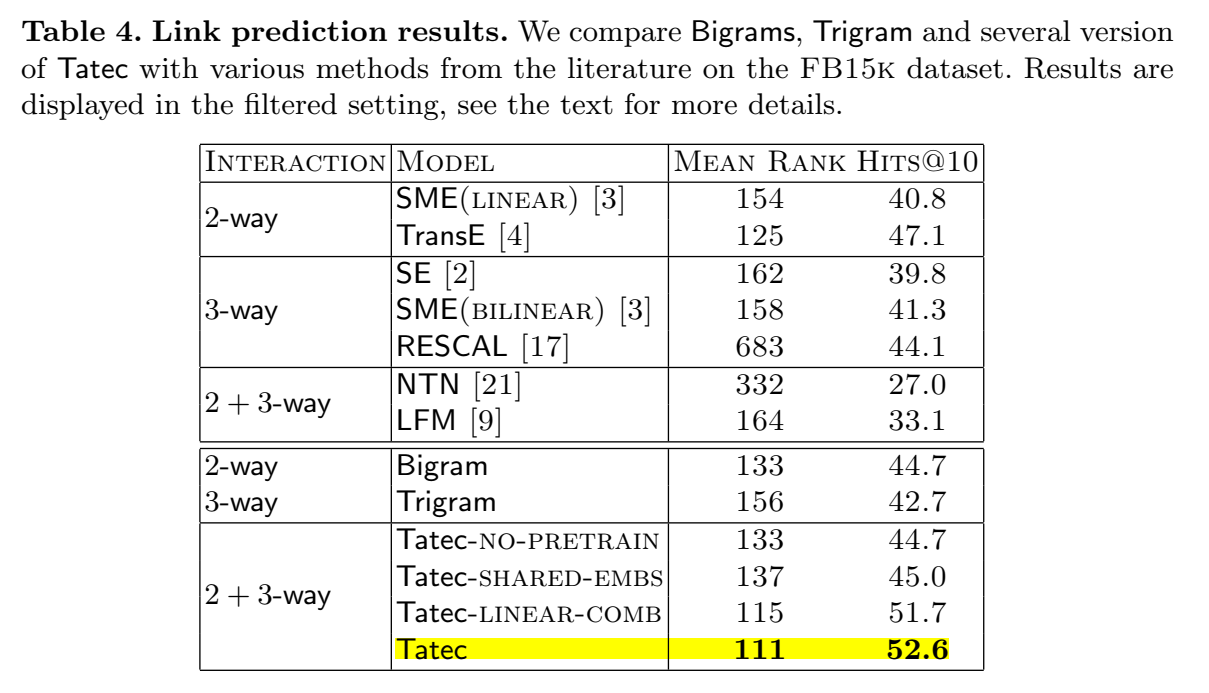
【总结】 文章提出了 TATEC，一种新的方法用于链接预测，将二元和三元交互项进行组合，两部分分别进行单独预训练，然后进行联合微调。

双线性模型（三）（MLP、TATEC） - 胡萝不青菜 - 博客园