2020 级考研管理类联考数学真题

一、问题求解（本大题共 15 小题，每小题 3 分，共 45 分）下列每题给出 5 个选项中，只有一个是符合要求的，请在答题卡上将所选择的字母涂黑。

1、某产品去年涨价 10%，今年涨价 20%，则产品这两年涨价（ ）
A.15%
B.16%
C.30%
D.32%
E.33%

2、设A={$x||x-a|＜1，x\in R$}，B={$x||x-b|＜2，x\in R$}，则 A ⊂ B 的充分必要条件是（ ）
A.$|a-b|\le 1$
B.$|a-b|\ge 1$
C.$|a-b|＜1$
D.$|a-b|＞1$
E.$|a-b|=1$

3、一项考试的总成绩由甲乙丙三部分组成：总成绩=甲成绩×30% +乙成绩×20% +丙成绩50% ，考试通过的标准是：每部分≥50 分，且总成绩≥60 分。已知某人甲成绩 70 分，乙成绩 75 分，且通过了这项考试，则此人丙成绩的分数至少是（ ）
A.48
B.50
C.55
D.60
E.62

4、从 1 至 10 这 10 个整数中任取 3 个数，恰有 1 个质数的概率是（ ）
A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{5}{12}$
D. $\frac{2}{5}$
E.$\frac{1}{120}$

5、若等差数列{$a_n$} 满足$a_1=8$，且$a_2+a_4=a_1$，则{$a_n$} 的前n 项和的最大值为（ ）
A.16
B.17
C.18
D.19
E.20

6、已知实数 x 满足$x^2+\frac{1}{x^2}-\frac{3}{x}+2=0$，则$x^3+\frac{1}{x^3}=$（ ）
A.12
B.15
C.18
D.24
E.27

7、设实数 x, y 满足$|x-2|+|y-2|\le 2$，则$x^2+y^2$的取值范围是（ ）
A.[2,18]
B.[2, 20]
C.[2, 36]
D.[4,18]
E.[4, 20]

8、某网店对单价为 55 元、75 元、80 元的三种商品进行促销，促销策略是每单满 200 元减m元，如果每单减m 后实际售价均不低于原价的 8 折，那么m 的最大值为（ ）
A.40
B.41
C.43
D.44
E.48

9、某人在同一观众群中调查了对五部电影的看法，得到如下数据：

电影	第一部	第二部	第三部	第四部	第五部
好评率	0.25	0.5	0.3	0.8	0.4
差评率	0.75	0.5	0.7	0.2	0.6

据此数据，观众意见分歧较大的两部影片依次是（ ）
A.一三
B.二三
C.二五
D.四一
E.四二

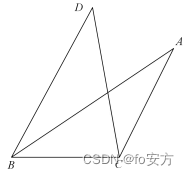
10、如图，在△ABC 中，∠ABC=$30^0$ ，将线段 AB 绕 B 点旋转至 DB ，使∠DBC=$60^0$，则△DBC与△ABC 的面积之比为（ ）
A.1
B.$\sqrt{2}$
C.2
D.$\frac{\sqrt{3}}{2}$
E.$\sqrt{3}$

11、已知数列{$a_n$}满足$a_1=1$，$a_2=2$，且$a_{n+2}=a_{n+1}-a_n(n=1,2,3,...)$，则$a_{100}$=（ ）
A.1
B.-1
C.2
D.-2
E.0

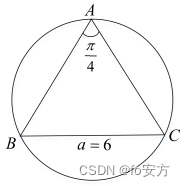
12、如图，圆O 的内接三角形 ABC 是等腰三角形，底边BC=6，顶角为$\frac{\pi }{4}$，则圆O 的面积为（ ）
A.12π
B.16π
C.18π
D.32π
E.36π

13.甲、乙分别从 A、B 两点同时出发相向而行，多次往返行走，AB 距离 1800m，甲的速度为 100m/min ，乙的速度为 80m/min ，则两人第三次相遇时，甲距其出发点（ ）米
A.600
B.900
C.1000
D.1400
E.1600

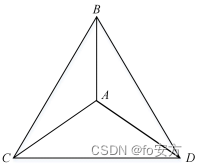
14.节点 A, B, C, D 两两相连，从一个节点沿线段到另一个节点当作 1 步，若机器人从节点 A出发，随机走了 3 步，则机器人从未经过节点C 的概率为（ ）

A.$\frac{4}{9}$
B. $\frac{11}{27}$
C. $\frac{10}{27}$
D. $\frac{19}{27}$
E. $\frac{8}{27}$

15、某科室有 4 名男职员，2 名女职员，若将这 6 名职员分为 3 组，每组两人，且女职员不同组，则分法有（ ）种
A.4
B.6
C.9
D.12
E.15

二．条件充分性判断：（第 16-25 小题，每小题 3 分，共 30 分）

要求判断每题给出的条件（1）和（2）能否充分支持题干所陈述的结论，A、B、C、D、E 五个选项为判断结果，请选择一项符合试题要求的判断，请在答题卡上将所选的字母涂黑。
（A） 条件（1）充分，但条件（2）不充分
（B） 条件（2）充分，但条件（1）不充分
（C） 条件（1）和（2）都不充分，但联合起来充分
（D） 条件（1）充分，条件（2）也充分
（E） 条件（1）不充分，条件（2）也不充分，联合起来仍不充分

16、在△ABC 中，∠B=$60^0$，则$c/a＞2$
（1）$\angle C＜90^0$
（2）$\angle C＞90^0$

17、曲线 上的点到$x^2+y^2=2x+2y$上的点到$ax+by+\sqrt{2}=0$的距离最小值大于 1。
（1）$a^2+b^2=1$
（2）$a＞0，b＞0$

18、若a, b, c 是实数，则能确定a, b, c 的最大值。
（1）已知a, b, c 的平均值
（2）已知a, b, c 的最小值

19、甲、乙两种品牌手机共有 20 部，从中任选 2 部，则恰有 1 部甲品牌手机的概率大于$\frac{1}{2}$。
（1）甲手机不少于 8 部
（2）乙手机大于 7 部

20、共有n 辆车，则能确定人数。
（1）若每辆车 20 座，1 车未满
（2）若每辆车 12 座，则少 10 个座

21、在长方体中，能确定长方体的体对角线长度。
（1）已知长方体一个顶点的三个面的面积
（2）已知长方体一个顶点的三个面的面对角线的长度

22、已知甲、乙、丙三人共捐款 3500 元，则能确定每人的捐款金额.
（1）三人的捐款金额各不相同
（2）三人的捐款金额都是 500 的倍数

23、设函数$f(x)=(ax-1)(x-4)$，则在 x = 4 左侧附近有$f(x)＜0$。
（1）$\frac{a＞1}{4}$
（2）$a＜4$

24、设a, b 是正实数，则$\frac{1}{a}$+$\frac{1}{b}$存在最小值.
（1）已知ab的值
（2）已知a, b 是方程$x^2-(a+b)x+2=0$的两个不同实根

25、设a, b, c, d 是正实数，则$\sqrt{a}+\sqrt{b}\le \sqrt{2(b+c)}$
（1）a + d = b + c
（2）ad = bc