文章目录

周赛351
- [2748. 美丽下标对的数目](https://leetcode.cn/problems/number-of-beautiful-pairs/)
- - 模拟
  - O(10n)做法
- [2749. 得到整数零需要执行的最少操作数](https://leetcode.cn/problems/minimum-operations-to-make-the-integer-zero/)
- - 枚举答案
- [2750. 将数组划分成若干好子数组的方式](https://leetcode.cn/problems/ways-to-split-array-into-good-subarrays/)
- - 乘法原理 + 同向双指针（转换题意）
  - 隔板问题
- [2751. 机器人碰撞](https://leetcode.cn/problems/robot-collisions/)
- - 用栈模拟（行星碰撞）

周赛351

2748. 美丽下标对的数目

难度简单0

给你一个下标从 0 开始的整数数组 nums 。如果下标对 i、j 满足 0 ≤ i < j < nums.length ，如果 nums[i] 的 第一个数字 和 nums[j] 的 最后一个数字 互质，则认为 nums[i] 和 nums[j] 是一组 美丽下标对 。

返回 nums 中 美丽下标对 的总数目。

对于两个整数 x 和 y ，如果不存在大于 1 的整数可以整除它们，则认为 x 和 y 互质。换而言之，如果 gcd(x, y) == 1 ，则认为 x 和 y 互质，其中 gcd(x, y) 是 x 和 k 最大公因数 。

示例 1：

输入：nums = [2,5,1,4]
输出：5
解释：nums 中共有 5 组美丽下标对：
i = 0 和 j = 1 ：nums[0] 的第一个数字是 2 ，nums[1] 的最后一个数字是 5 。2 和 5 互质，因此 gcd(2,5) == 1 。
i = 0 和 j = 2 ：nums[0] 的第一个数字是 2 ，nums[1] 的最后一个数字是 1 。2 和 5 互质，因此 gcd(2,1) == 1 。
i = 1 和 j = 2 ：nums[0] 的第一个数字是 5 ，nums[1] 的最后一个数字是 1 。2 和 5 互质，因此 gcd(5,1) == 1 。
i = 1 和 j = 3 ：nums[0] 的第一个数字是 5 ，nums[1] 的最后一个数字是 4 。2 和 5 互质，因此 gcd(5,4) == 1 。
i = 2 和 j = 3 ：nums[0] 的第一个数字是 1 ，nums[1] 的最后一个数字是 4 。2 和 5 互质，因此 gcd(1,4) == 1 。
因此，返回 5 。

示例 2：

输入：nums = [11,21,12]
输出：2
解释：共有 2 组美丽下标对：
i = 0 和 j = 1 ：nums[0] 的第一个数字是 1 ，nums[1] 的最后一个数字是 1 。gcd(1,1) == 1 。
i = 0 和 j = 2 ：nums[0] 的第一个数字是 1 ，nums[1] 的最后一个数字是 2 。gcd(1,2) == 1 。
因此，返回 2 。

提示：

2 <= nums.length <= 100
1 <= nums[i] <= 9999
nums[i] % 10 != 0

模拟

class Solution {
    public int countBeautifulPairs(int[] nums) {
        int ans = 0;
        int n = nums.length;
        for(int i = 0; i < n; i++){
            for(int j = i+1; j < n; j++){
                int p = nums[i], q = nums[j];
                while(p >= 10) p /= 10;
                q = q % 10;
                if(gcd(p, q) == 1) ans += 1;
            }
        }
        return ans;
    }

    public int gcd(int x, int y){
        return y == 0 ? x : gcd(y, x % y);
    }
}

O(10n)做法

class Solution {
    // 同两数之和，用哈希表统计前面第一个数字在[0,9]的出现次数
    public int countBeautifulPairs(int[] nums) {
        int[] cnt = new int[10];
        int ans = 0;
        for(int num : nums){
            for(int y = 1; y < 10; y++){
                if(gcd(num % 10, y) == 1) 
                    ans += cnt[y];
            }
            while(num >= 10) num /= 10;
            cnt[num] += 1;
        }
        return ans;
    }

    public int gcd(int x, int y){
        return y == 0 ? x : gcd(y, x % y);
    }
}

2749. 得到整数零需要执行的最少操作数

难度中等4

给你两个整数：num1 和 num2 。

在一步操作中，你需要从范围 [0, 60] 中选出一个整数 i ，并从 num1 减去 2i + num2 。

请你计算，要想使 num1 等于 0 需要执行的最少操作数，并以整数形式返回。

如果无法使 num1 等于 0 ，返回 -1 。

示例 1：

输入：num1 = 3, num2 = -2
输出：3
解释：可以执行下述步骤使 3 等于 0 ：
- 选择 i = 2 ，并从 3 减去 22 + (-2) ，num1 = 3 - (4 + (-2)) = 1 。
- 选择 i = 2 ，并从 1 减去 22 + (-2) ，num1 = 1 - (4 + (-2)) = -1 。
- 选择 i = 0 ，并从 -1 减去 20 + (-2) ，num1 = (-1) - (1 + (-2)) = 0 。
可以证明 3 是需要执行的最少操作数。

示例 2：

输入：num1 = 5, num2 = 7
输出：-1
解释：可以证明，执行操作无法使 5 等于 0 。

提示：

1 <= num1 <= 109
-109 <= num2 <= 109

枚举答案

题解：https://leetcode.cn/problems/minimum-operations-to-make-the-integer-zero/solution/mei-ju-da-an-pythonjavacgo-by-endlessche-t4co/

class Solution {
    // 从小到大枚举答案
    // 假设操作了k次，那么操作后 num1 变成 num1 - num2*k 再减去 k个2^i
    //          问题变成：num1-num2*k能否拆分成k个2^i之和
    // 设 x = num1 - num2*k
    //      如果 x < 0, 无解
    //      否则如果 x < k, 那么即使每次操作取i = 0, 也至少要把 x 拆分成 k 个 1 之和，这是不可能的
    //      否则如果 x 中二进制 1的个数大于k，也无法拆分成 k 个2^i之和，无解
    //      否则分解方案一定存在，返回k
    public int makeTheIntegerZero(int num1, int num2) {
        for(long k = 1; k <= num1 - num2*k; k++){
            if(k >= Long.bitCount(num1 - num2 * k))
                return (int)k;
        }    
        return -1;
    }
}

为什么x中二进制1的个数小于k的时候就是有解的?

因为每一个 2^i 都可以拆分成 2个 2^(i-1) 的和，相当于1次操作我可以选择性地让其裂变成2次操作，总体操作数的增量是1，这样我始终可以慢慢递增操作数直到达到我想要的k。举个例子二进制数1001，k是3，我就可以把2^3拆成2个2^2，从而使操作数恰好为3。而如果二进制数是11，k是6，这个怎么拆呢？这就属于x < k 的情况，已经在前面排除掉了

2750. 将数组划分成若干好子数组的方式

难度中等0

给你一个二元数组 nums 。

如果数组中的某个子数组恰好只存在一个值为 1 的元素，则认为该子数组是一个 好子数组 。

请你统计将数组 nums 划分成若干 好子数组 的方法数，并以整数形式返回。由于数字可能很大，返回其对 109 + 7 取余之后的结果。

子数组是数组中的一个连续非空元素序列。

示例 1：

输入：nums = [0,1,0,0,1]
输出：3
解释：存在 3 种可以将 nums 划分成若干好子数组的方式：
- [0,1] [0,0,1]
- [0,1,0] [0,1]
- [0,1,0,0] [1]

示例 2：

输入：nums = [0,1,0]
输出：1
解释：存在 1 种可以将 nums 划分成若干好子数组的方式：
- [0,1,0]

提示：

1 <= nums.length <= 105
0 <= nums[i] <= 1

乘法原理 + 同向双指针（转换题意）

class Solution {
    // 两个相邻的1之间只有 0个数+1 中分割方法
    // 乘法原理 + 同向双指针,双指针找到每一个相邻1之间有多少个0
    private static final int MOD = (int)1e9+7;
    public int numberOfGoodSubarraySplits(int[] nums) {
        double ans = 1.0;
        int left = 0, n = nums.length;
        while(left < n && nums[left] == 0) left++; // 找到第一个1
        if(left == n) return 0;
        int right = left + 1;
        while(right < n){
            while(right < n && nums[right] == 0)
                right++;
            // 此时 left 和 right 都指向1
            if(right != n){
                ans = (ans * (right - left)) % MOD;
                left = right;
                right += 1;
            }
        }
        return (int)ans;
    }
}

另外一种写法

class Solution {
    public int numberOfGoodSubarraySplits(int[] nums) {
        final long MOD = (long) 1e9 + 7;
        long ans = 1;
        int pre = -1, n = nums.length;
        for (int i = 0; i < n; i++) {
            if (nums[i] == 0) continue;
            if (pre >= 0) ans = ans * (i - pre) % MOD;
            pre = i;
        }
        return pre < 0 ? 0 : (int) ans;
    }
}

隔板问题

数学题，任意两个1之间0的数目乘积就是答案，本质上是枚举两个子数组的边界自由度，“2147题分隔长廊的方案数”和这个题一样。

这是个典型的隔板问题，分割子数组相当于在相邻两个1之间的位置放入隔板，问有几种放法

显然总数等于sum(Π(a_{i+1} - a{i}))

class Solution:
    def numberOfGoodSubarraySplits(self, nums: List[int]) -> int:
        mod = 10 ** 9 + 7
        pos = []
        for i, v in enumerate(nums):
            if v:
                pos.append(i)
        if len(pos) == 0: return 0
        ans = 1
        for i in range(1, len(pos)):
            cnt = pos[i] - pos[i-1]
            ans = ans * cnt % mod
        return ans

2751. 机器人碰撞

难度困难0

现有 n 个机器人，编号从 1 开始，每个机器人包含在路线上的位置、健康度和移动方向。

给你下标从 0 开始的两个整数数组 positions、healths 和一个字符串 directions（directions[i] 为 ‘L’ 表示向左或 ‘R’ 表示向右）。 positions 中的所有整数 互不相同 。

所有机器人以 相同速度 同时沿给定方向在路线上移动。如果两个机器人移动到相同位置，则会发生碰撞。

如果两个机器人发生碰撞，则将 健康度较低 的机器人从路线中移除，并且另一个机器人的健康度 减少 1 。幸存下来的机器人将会继续沿着与之前相同的方向前进。如果两个机器人的健康度相同，则将二者都从路线中移除。

请你确定全部碰撞后幸存下的所有机器人的 健康度 ，并按照原来机器人编号的顺序排列。即机器人 1 （如果幸存）的最终健康度，机器人 2 （如果幸存）的最终健康度等。如果不存在幸存的机器人，则返回空数组。

在不再发生任何碰撞后，请你以数组形式，返回所有剩余机器人的健康度（按机器人输入中的编号顺序）。

**注意：**位置 positions 可能是乱序的。

示例 1：

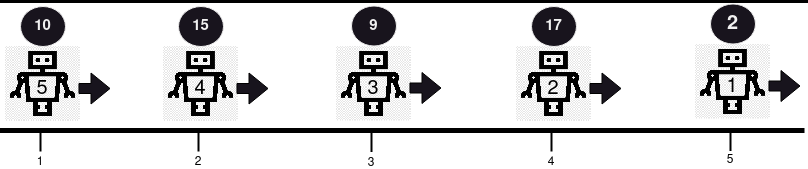
输入：positions = [5,4,3,2,1], healths = [2,17,9,15,10], directions = "RRRRR"
输出：[2,17,9,15,10]
解释：在本例中不存在碰撞，因为所有机器人向同一方向移动。所以，从第一个机器人开始依序返回健康度，[2, 17, 9, 15, 10] 。

示例 2：

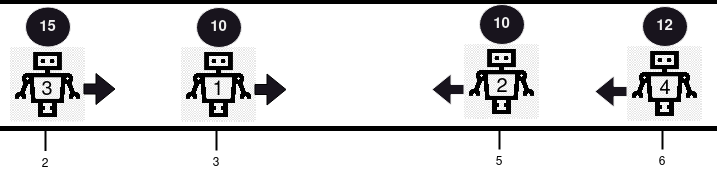
输入：positions = [3,5,2,6], healths = [10,10,15,12], directions = "RLRL"
输出：[14]
解释：本例中发生 2 次碰撞。首先，机器人 1 和机器人 2 将会碰撞，因为二者健康度相同，二者都将被从路线中移除。接下来，机器人 3 和机器人 4 将会发生碰撞，由于机器人 4 的健康度更小，则它会被移除，而机器人 3 的健康度变为 15 - 1 = 14 。仅剩机器人 3 ，所以返回 [14] 。

示例 3：

输入：positions = [1,2,5,6], healths = [10,10,11,11], directions = "RLRL"
输出：[]
解释：机器人 1 和机器人 2 将会碰撞，因为二者健康度相同，二者都将被从路线中移除。机器人 3 和机器人 4 将会碰撞，因为二者健康度相同，二者都将被从路线中移除。所以返回空数组 [] 。

提示：

1 <= positions.length == healths.length == directions.length == n <= 105
1 <= positions[i], healths[i] <= 109
directions[i] == 'L' 或 directions[i] == 'R'
positions 中的所有值互不相同

用栈模拟（行星碰撞）

同 735. 行星碰撞

class Solution {
    public List<Integer> survivedRobotsHealths(int[] positions, int[] healths, String directions) {
        int n = positions.length;
        int[][] robots = new int[n][4];
        for(int i = 0; i < n; i++){
            robots[i][0] = i;
            robots[i][1] = positions[i];
            robots[i][2] = healths[i];
            robots[i][3] = (directions.charAt(i) == 'L') ? -1 : 1;
        }
        // 按照线路上的位置进行排序
        Arrays.sort(robots, (a, b) -> a[1] - b[1]);
        // 维护一个栈，同 735. 行星碰撞
        Deque<Integer> dq = new ArrayDeque<>();
        for(int i = 0; i < n; i++){
            if(robots[i][3] > 0){ // 往右，直接入栈
                dq.push(i);
            }else{
                boolean alive = true; // 标记当前元素n是否存活
                while(alive && !dq.isEmpty() && robots[dq.peek()][3] > 0){
                    // 如果两个机器人的健康度相同，则将二者都从路线中移除。
                    if(robots[i][2] == robots[dq.peek()][2]){
                        alive = false;
                        dq.poll();
                    // 如果两个机器人发生碰撞，则将 健康度较低 的机器人从路线中 移除 
                    //      并且另一个机器人的健康度 减少 1 
                    }else if(robots[i][2] > robots[dq.peek()][2]){
                        dq.poll();
                        robots[i][2] -= 1;
                    }else{
                        alive = false;
                        robots[dq.peek()][2] -= 1;
                    }
                }
                if(alive) dq.push(i);
            }
        }
        // 栈中的机器人都是存活的，将其按照编号顺序排序，然后将健康值放入答案中
        List<int[]> list = new ArrayList<>();
        while(!dq.isEmpty()){
            list.add(robots[dq.poll()]);
        } 
        Collections.sort(list, (a, b) -> a[0] - b[0]);
        List<Integer> ans = new ArrayList<>();
        for(int i = 0; i < list.size(); i++){
            ans.add(list.get(i)[2]);
        }
        return ans;
    }
}