哑变量处理
特点:对于一个类别型特征,若其取值有m个,则经过哑变量处理后就变成了m个二元特征,并且这些特征互斥,每次只有一个激活,这使得数据变得稀疏。
get_dummise()函数:
pd.get_dummies(data['dishes_name'])#进行哑变量处理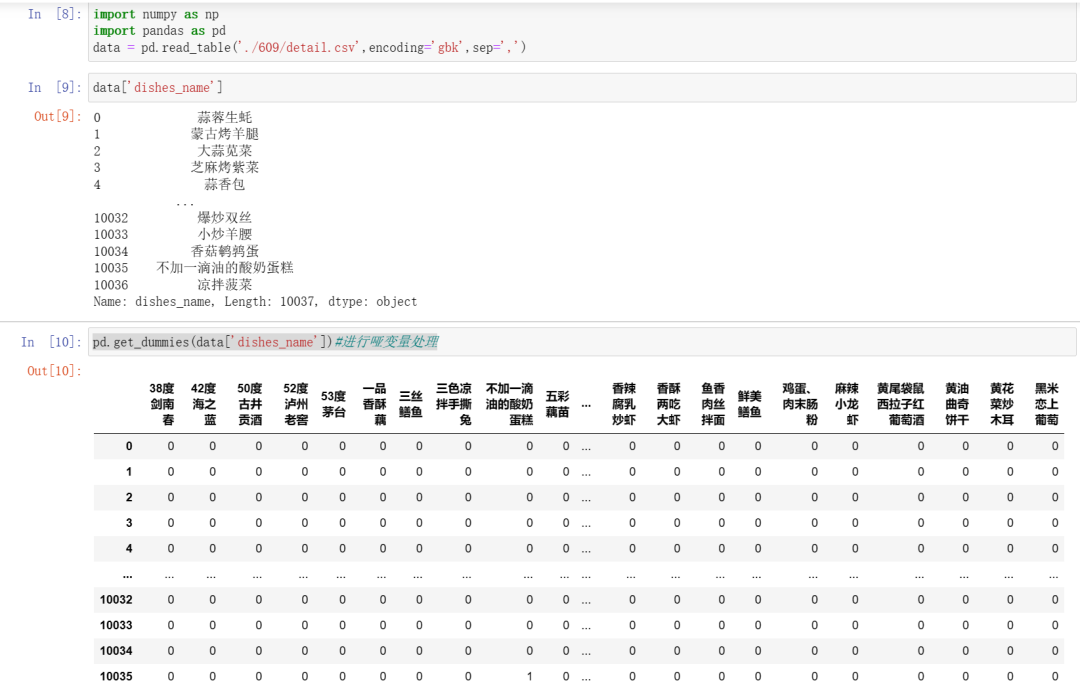
离散化【等宽法、等频法、基于聚类分析的方法】
某些模型算法,特别是某些分类算法如ID3决策树算法和Apriori算法等,要求数据是离散的,此时就需要将联系型特征(数值型)变换成离散型特征。
等宽法:
将数据的值域分成具有相同宽度的区间,区间的个数由数据本身的特点决定或者用户指定,与制作频率分布表类似;
对数据分布具有较高要求。
cut()函数:
pd.cut(data['amounts'],bins=5).value_counts()#划分为5类(取值不均匀)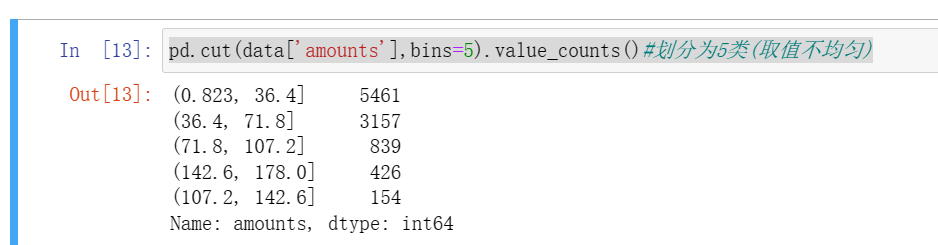
等频法:
cut函数虽然不能够直接现实等频离散化,但是可以通过定义将相同数量的记录放进每个区间;
等频法离散化的方法相比较于等宽法离散化而言,避免了类分布不均匀的问题。
def samefreq(data,k):#等频法w = data.quantile(np.arange(0,1+1/k,1/k))#前闭后开,步长1/kreturn pd.cut(data,w)samefreq(data['amounts'],k=5).value_counts()#对离散化做一下统计

基于聚类分析的方法
一维聚类的方法:
将连续型数据用聚类算法(K-Means算法等)进行聚类;
处理聚类得到的簇,将合并到一个簇的连续型数据做同一标记;
聚类分析的离散化方法需要用户指定簇的个数,用来决定产生的区间数。
聚类:
聚类的输入是一组未被标记的样本,聚类根据数据自身的距离或相似度将他们划分为若干组,划分的原则是组内样本最小化。
sklearn估计器:(拥有fit和predict两个方法)
fit():
实例:
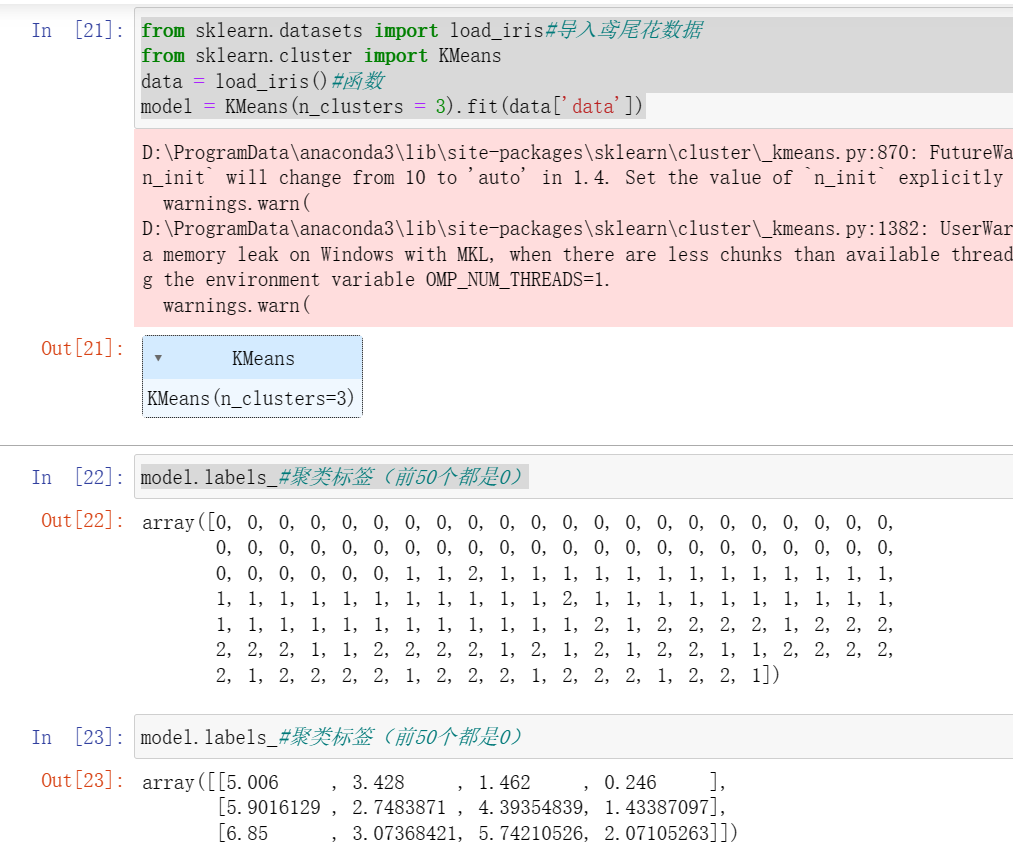
def samefreq(data,k):#等频法w = data.quantile(np.arange(0,1+1/k,1/k))#前闭后开,步长1/kreturn pd.cut(data,w)samefreq(data['amounts'],k=5).value_counts()#对离散化做一下统计from sklearn.datasets import load_iris#导入鸢尾花数据from sklearn.cluster import KMeansdata = load_iris()#函数model = KMeans(n_clusters = 3).fit(data['data'])model.labels_#聚类标签(前50个都是0)model.labels_#聚类标签(前50个都是0)
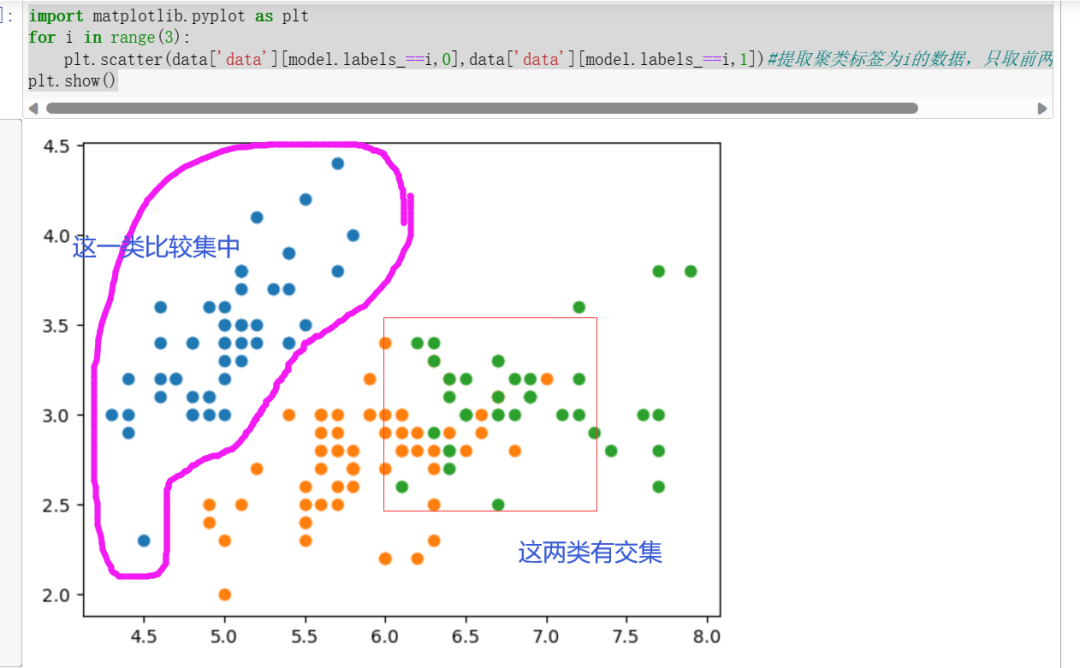
import matplotlib.pyplot as pltfor i in range(3):plt.scatter(data['data'][model.labels_==i,0],data['data'][model.labels_==i,1])#提取聚类标签为i的数据,只取前两列做图形绘制)plt.show()
聚类模型评价指标:
组内的对象相互之间是相似的,而不同组中的对象是不同的,即组内的相似性越大,组内差别越大,聚类效果就越好。
from sklearn.metrics import silhouette_scoresilhouette_score(data['data'],model.labels_)#0.5:聚类效果一般

from sklearn.metrics import silhouette_scorefor k in range(2,9):model = KMeans(n_clusters = k).fit(data['data'])print(k,silhouette_score(data['data'],model.labels_))#寻找最优k
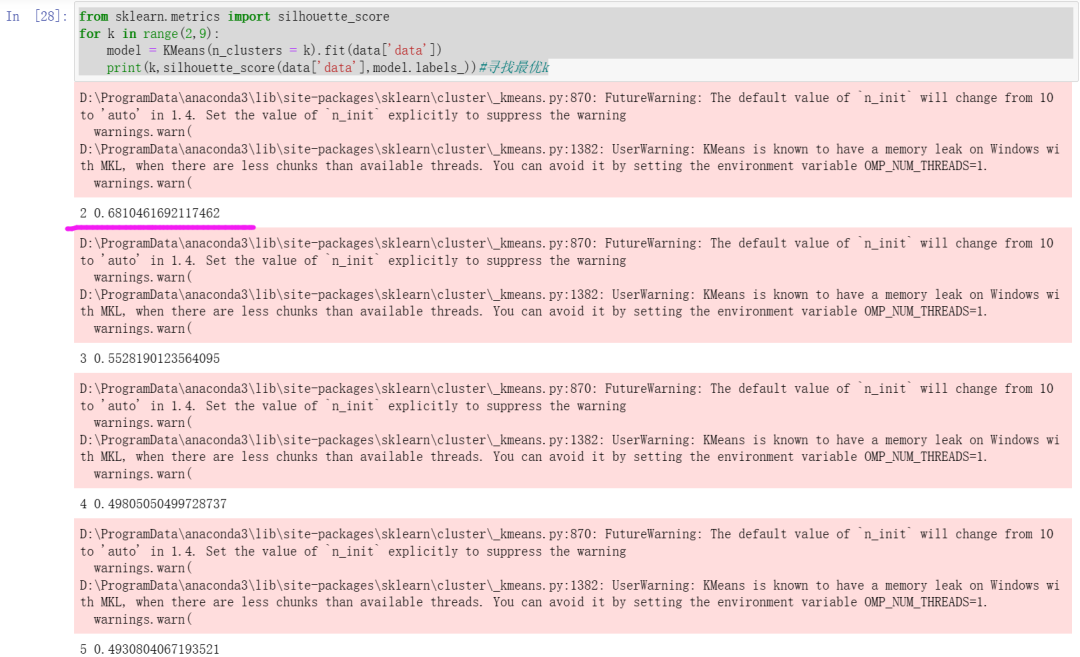
(可以看到k取2时,聚类效果最好)
另外,jupyter里面这个警告(红色的块)不在显示的方法:
输入代码,然后运行就ok:
import warningswarnings.filterwarnings("ignore")
得到效果:

分类算法的实现过程
在数据分析领域,分类算法有很多,其原理千差万别,有基于样本距离的最近邻算法,有基于特征信息熵的决策树,有基于bagging的随机森林,有基于boosting的梯度提升分类树,但其实现过程相差不大。
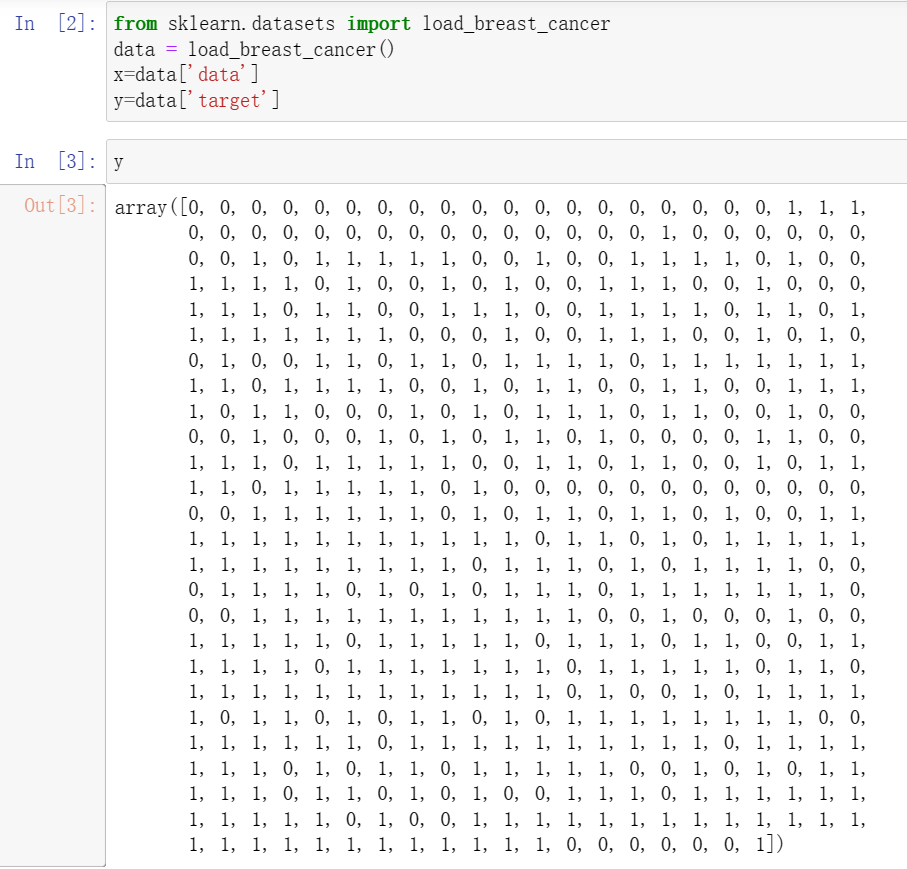
from sklearn.datasets import load_breast_cancerdata = load_breast_cancer()x=data['data']y=data['target']
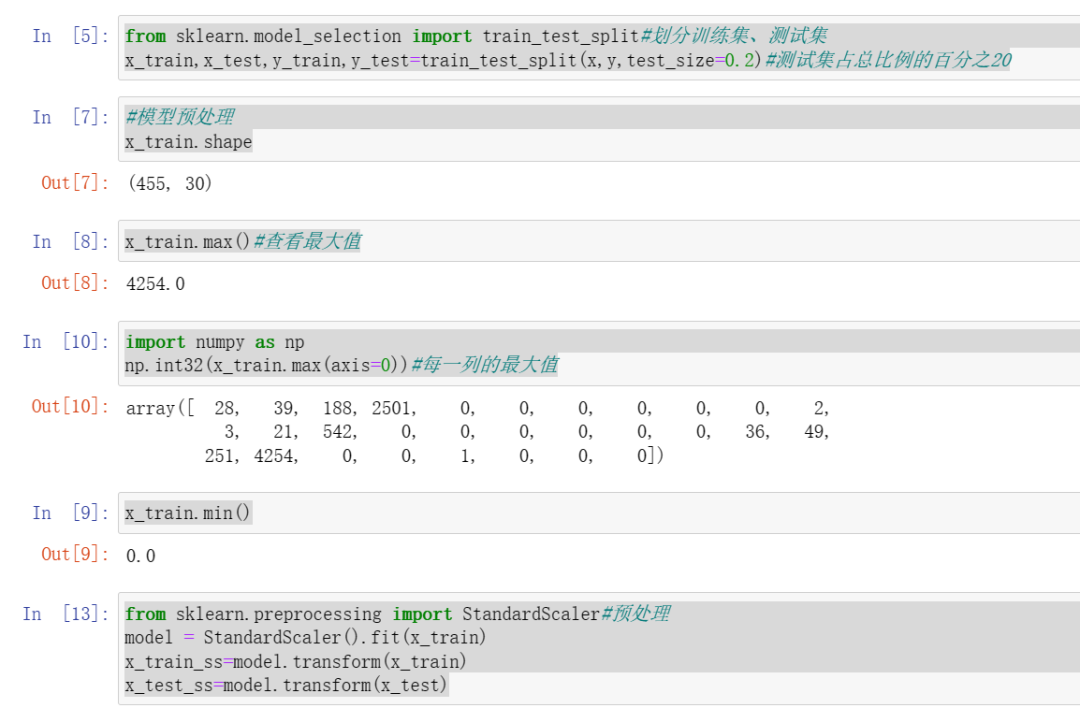
from sklearn.model_selection import train_test_split#划分训练集、测试集x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2)#测试集占总比例的百分之20#模型预处理x_train.shapex_train.max()#查看最大值import numpy as npnp.int32(x_train.max(axis=0))#每一列的最大值x_train.min()from sklearn.preprocessing import StandardScaler#预处理model = StandardScaler().fit(x_train)x_train_ss=model.transform(x_train)x_test_ss=model.transform(x_test)x_train_ss.max(axis=0)#分类模型构建from sklearn.svm import SVCmodel = SVC().fit(x_train_ss,y_train)y_pre=model.predict(x_test_ss)#构建好的数据
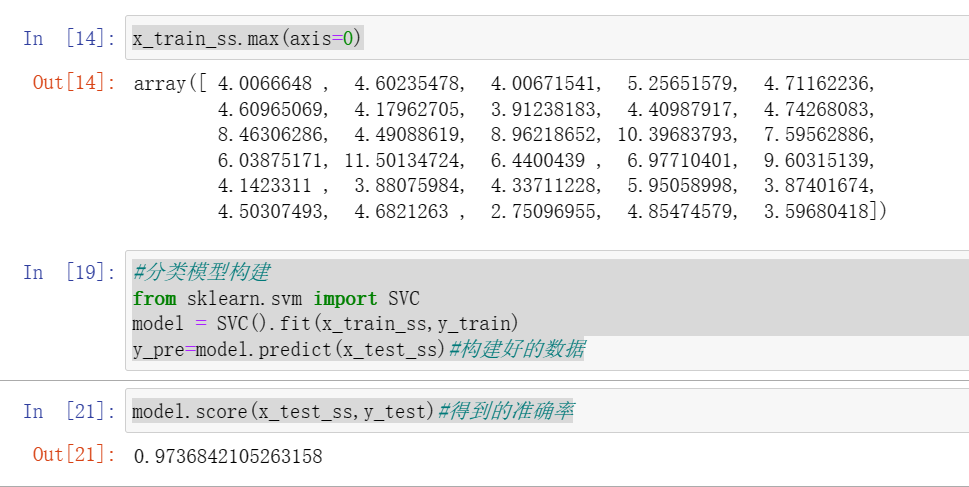
分类模型的评价指标
分类模型对测试集进行预测而得出的准确率并不能很好地反应模型的性能,为了有效判断一个预测模型的性表现,需要结合真实值,计算出精确率、召回率、F1值和Cohen's Kappa系数等指标来衡量。
from sklearn.metrics import recall_score,precision_score,f1_score,roc_curveprint(recall_score(y_test,y_pre))#召回率print(precision_score(y_test,y_pre))#准确率(与召回率相反)print(f1_score(y_test,y_pre))

(sklearn的metrics模块还提供了一个能够输出分类模型评价报告的函数classfication_report.)
ROC曲线

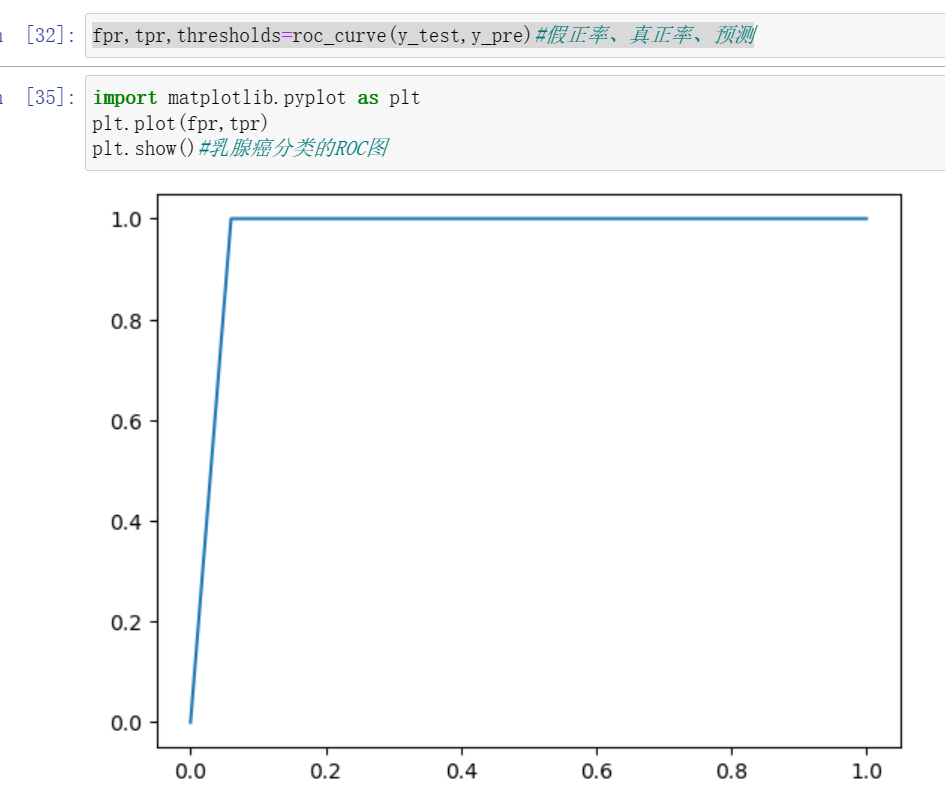
fpr,tpr,thresholds=roc_curve(y_test,y_pre)#假正率、真正率、预测import matplotlib.pyplot as pltplt.plot(fpr,tpr)plt.show()#乳腺癌分类的ROC图
回归分析方法
分为学习和预测两个步骤。学习是通过训练样本数据来拟合回归方程;预测是利用学习过程中拟合出的回归方程,将测试数据放入方程中求解。
回归模型的性能评估不同于分类模型,虽然都是对照真实值进行评估,但由于回归模型的预测结果和真实值都是连续的,所以不能够求取precision|recall和F1值等评价指标。