数据结构和算法详细内容

来源：黑马程序员Java数据结构与java算法

1.数据结构和算法概述

1.1什么是数据结构？

数据结构就是把数据元素按照一定的关系组织起来的集合，用来组织和存储数据

1.2数据结构分类

传统上，我们可以把数据结构分为逻辑结构和物理结构两大类。

逻辑结构分类：

逻辑结构是从具体问题中抽象出来的模型，是抽象意义上的结构，按照对象中数据元素之间的相互关系分类
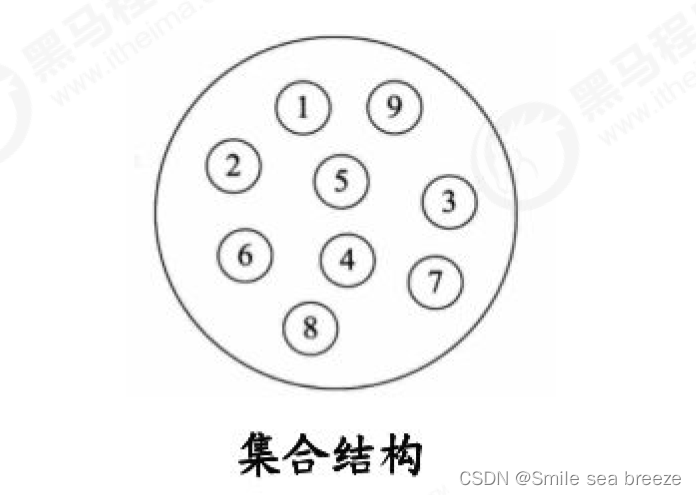
**a.集合结构：**集合结构中数据元素除了属于同一个集合外，他们之间没有任何其他的关系。

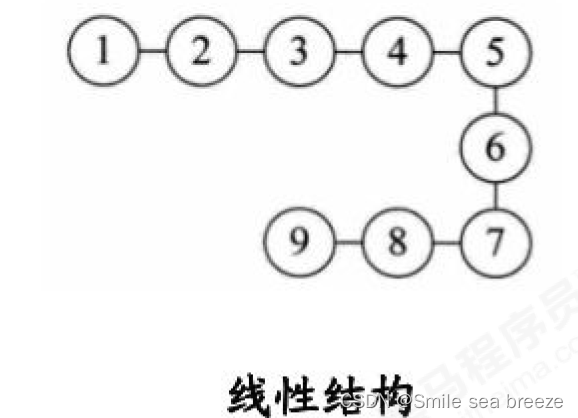
**b.线性结构：**线性结构中的数据元素之间存在一对一的关系

**c.树形结构：**树形结构中的数据元素之间存在一对多的层次关系

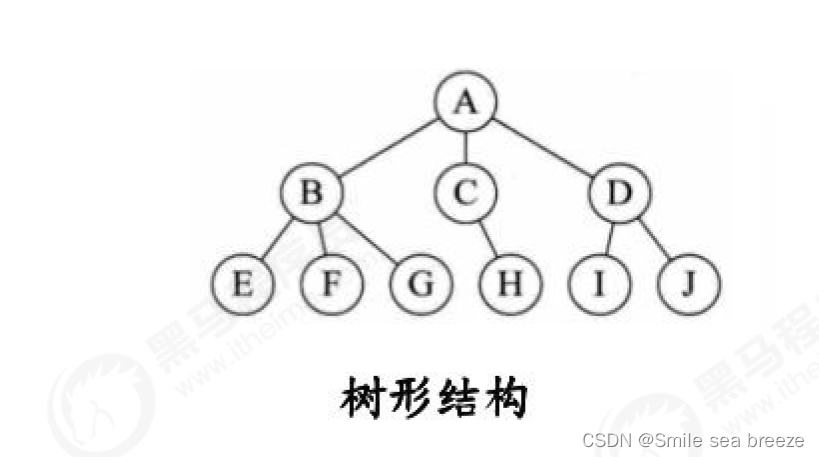
**d.图形结构：**图形结构的数据元素是多对多的关系
物

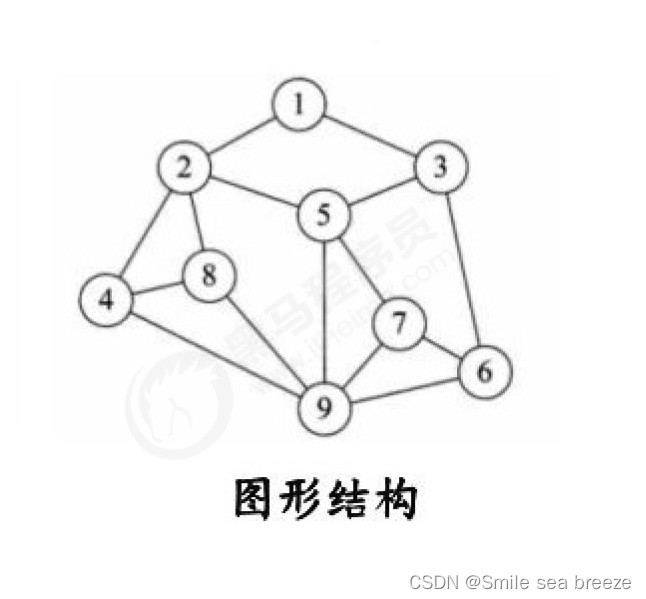
物理结构分类：

逻辑结构在计算机中真正的表示方式（又称为映像）称为物理结构，也可以叫做存储结构。常见的物理结构有顺序
存储结构、链式存储结构。

顺序存储结构：

把数据元素放到地址连续的存储单元里面，其数据间的逻辑关系和物理关系是一致的 ，比如我们常用的数组就是
顺序存储结构。

顺序存储结构存在一定的弊端，就像生活中排时也会有人插队也可能有人有特殊情况突然离开，这时候整个结构都
处于变化中，此时就需要链式存储结构。

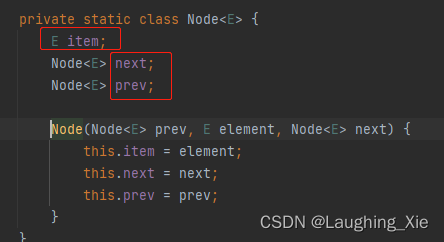
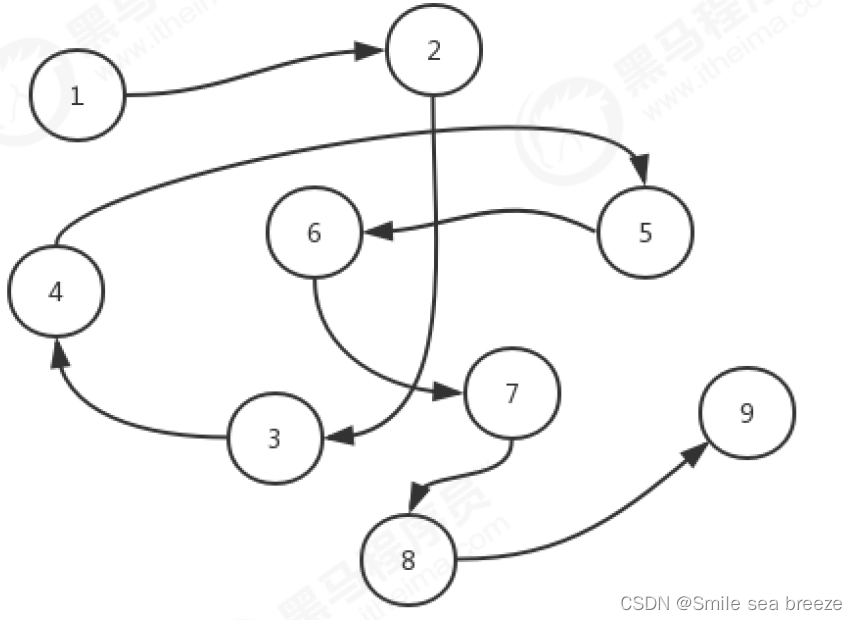
链式存储结构：

是把数据元素存放在任意的存储单元里面，这组存储单元可以是连续的也可以是不连续的。此时，数据元素之间并
不能反映元素间的逻辑关系，因此在链式存储结构中引进了一个指针存放数据元素的地址，这样通过地址就可以找
到相关联数据元素的位置

1.3 算法是什么？

根据一定的条件，对一些数据进行计算，得到需要的结果。

一个优秀的算法追求以下两个目标：
1.花最少的时间完成需求；
2.占用最少的内存空间完成需求；

2.算法分析

1.1算法的时间复杂度分析

在计算机程序编写前，依据统计方法对算法进行估算，经过总结，我们发现一个高级语言编写的程序程序在计算机
上运行所消耗的时间取决于下列因素：
1.算法采用的策略和方案；
2.编译产生的代码质量；
3.问题的输入规模(所谓的问题输入规模就是输入量的多少)；
4.机器执行指令的速度；

需求：
计算1到100的和。

第一种解法：

//如果输入量为n为1，则需要计算1次；
//如果输入量n为1亿，则需要计算1亿次；
public static void main(String[] args) {
	int sum = 0;//执行1次
	int n=100;//执行1次
	for (int i = 1; i <= n; i++) {//执行了n+1次
	sum += i;//执行了n次
}
System.out.println("sum=" + sum);
}

第二种解法：

//如果输入量为n为1，则需要计算1次；
//如果输入量n为1亿，则需要计算1次；
public static void main(String[] args) {
	int sum = 0;//执行1次
	int n=100;//执行1次
	sum = (n+1)*n/2;//执行1次
	System.out.println("sum="+sum);
}

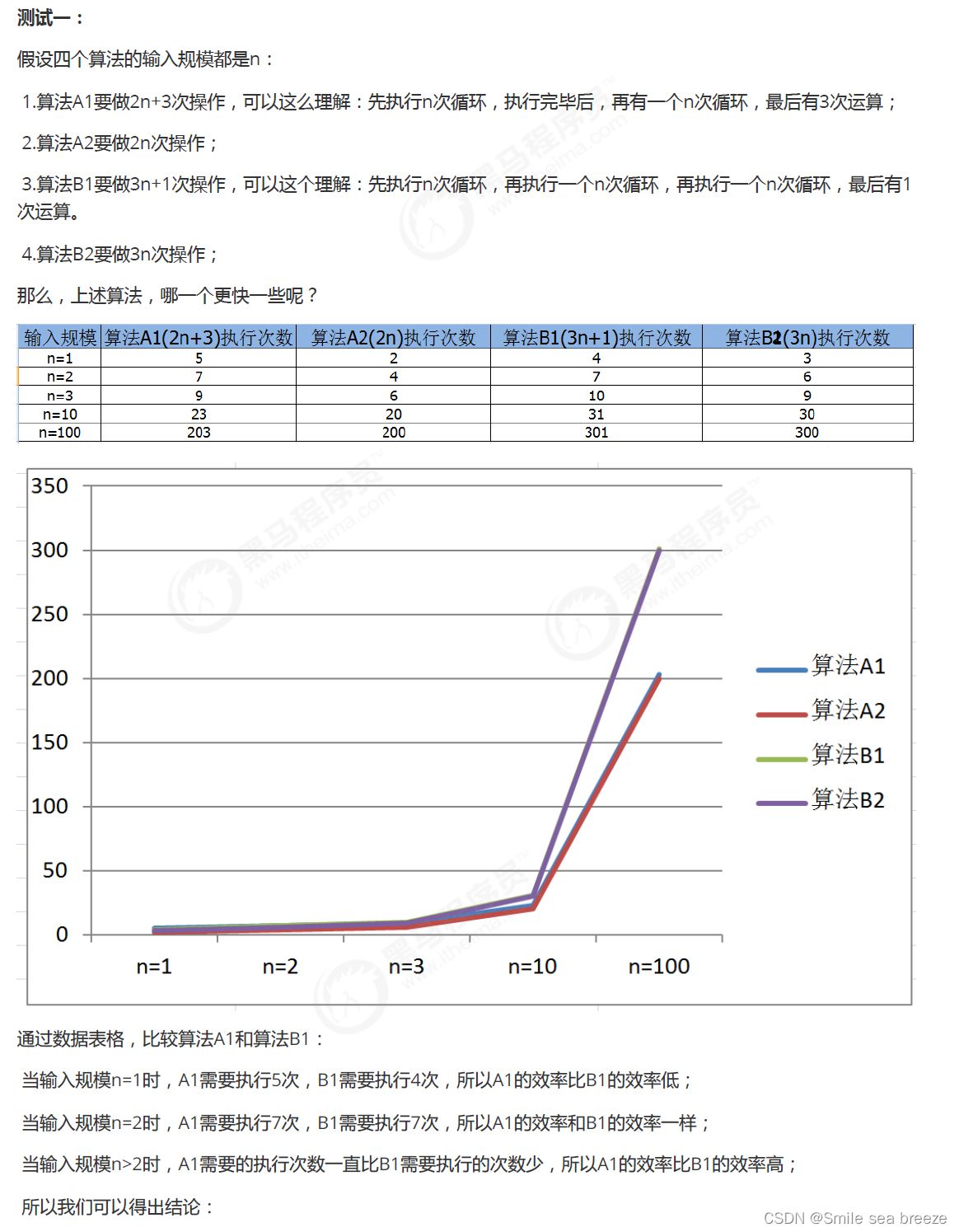
因此，当输入规模为n时，第一种算法执行了1+1+(n+1)+n=2n+3次；第二种算法执行了1+1+1=3次。如果我们把
第一种算法的循环体看做是一个整体，忽略结束条件的判断，那么其实这两个算法运行时间的差距就是n和1的差
距。
为什么循环判断在算法1里执行了n+1次，看起来是个不小的数量，但是却可以忽略呢？我们来看下一个例子：
需求：
计算100个1+100个2+100个3+…100个100的结果
代码：

public static void main(String[] args) {
	int sum=0;
	int n=100;
	for (int i = 1; i <=n ; i++) {
	for (int j = 1; j <=n ; j++) {
	sum+=i;
	}
}
System.out.println("sum="+sum);
}

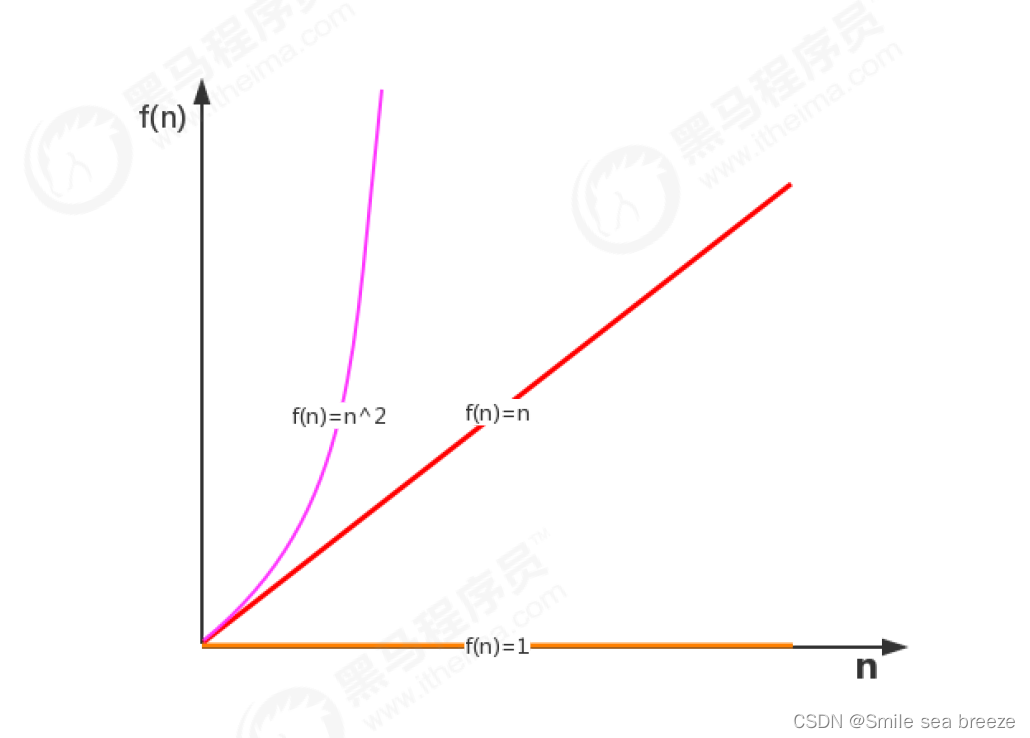
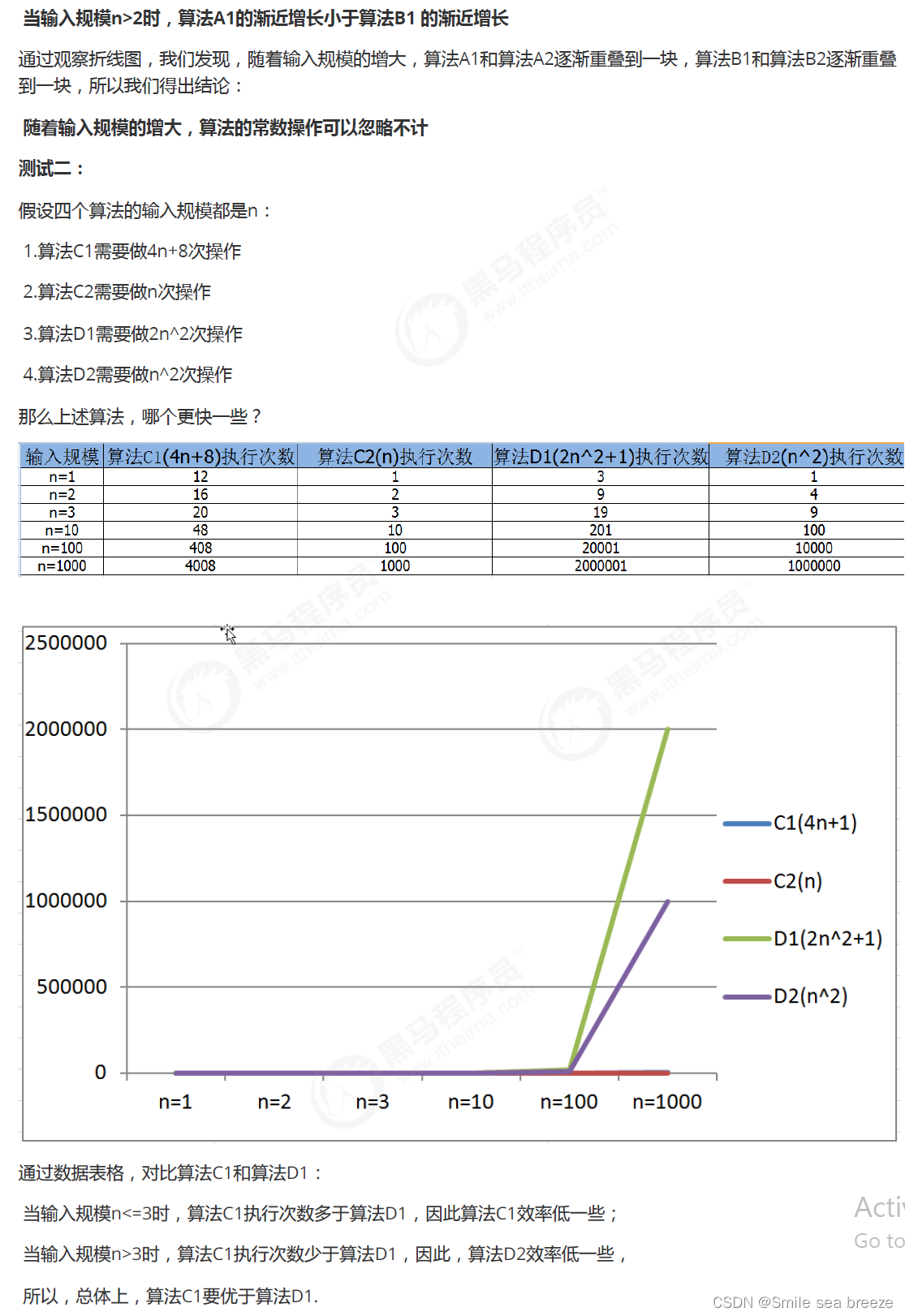
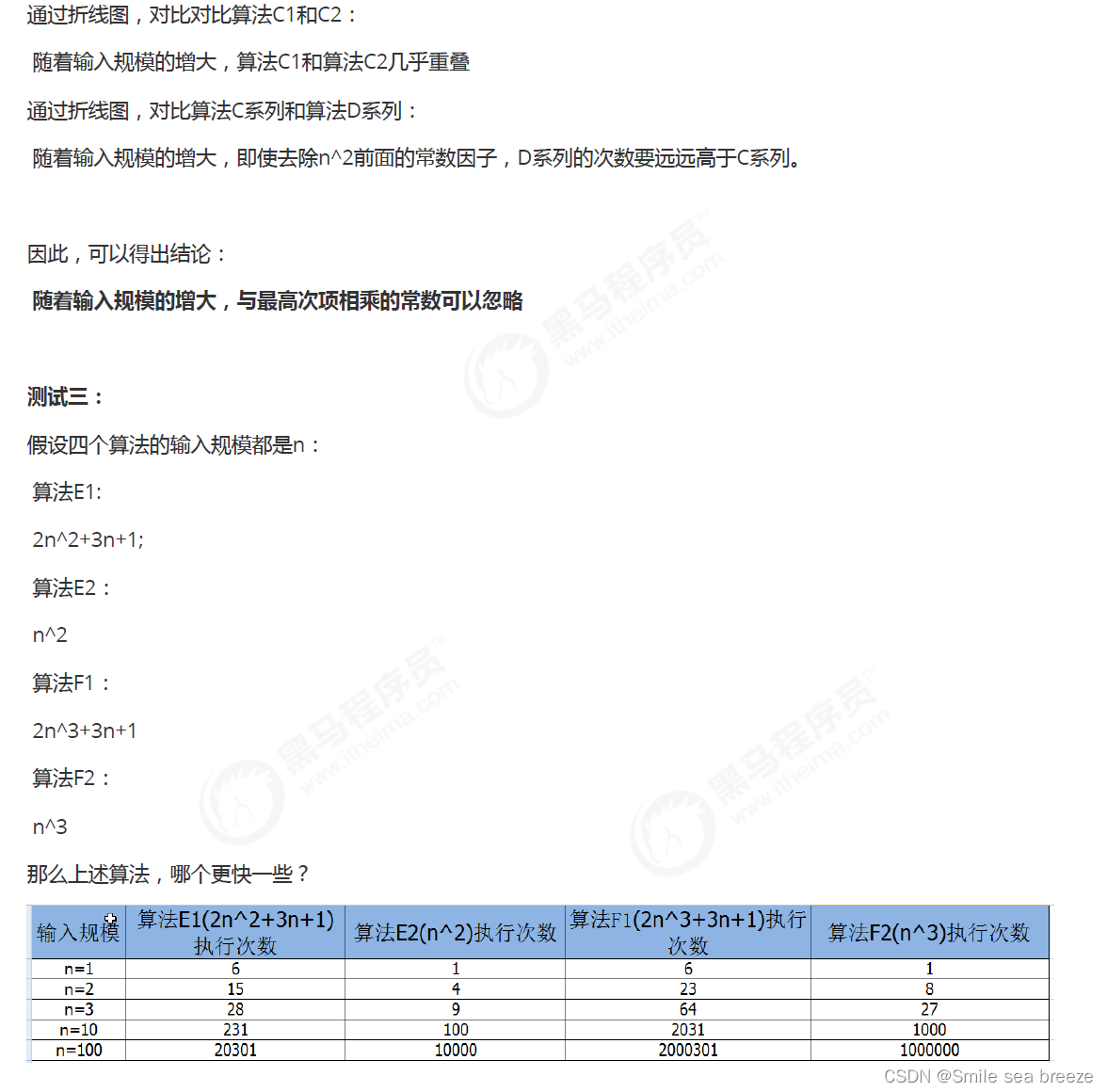
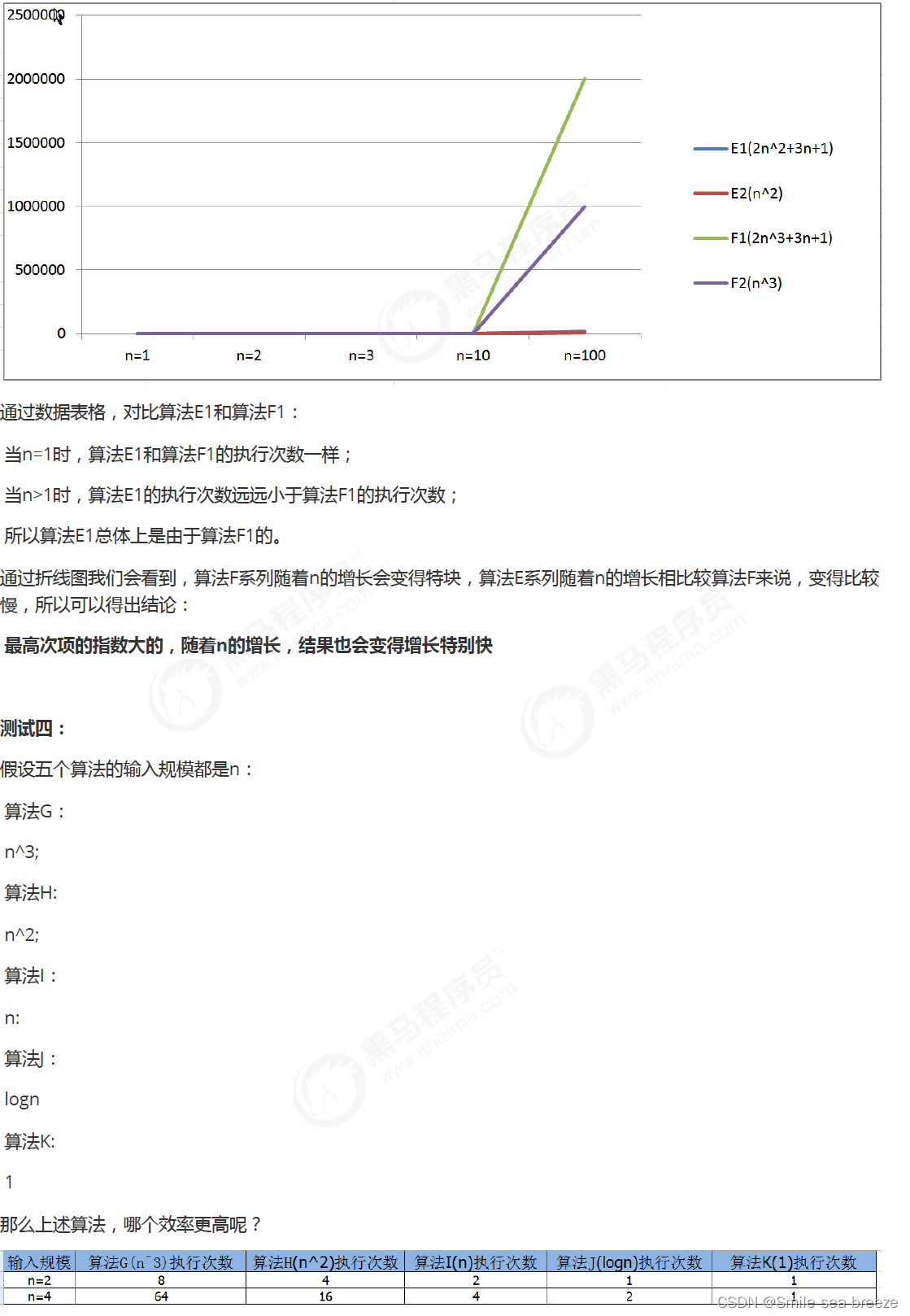
函数渐近增长
给定两个函数f(n)和g(n),如果存在一个整数N，使得对于所有的n>N,f(n)总是比g(n)大，那么我们说f(n)的增长渐近
快于g(n)。

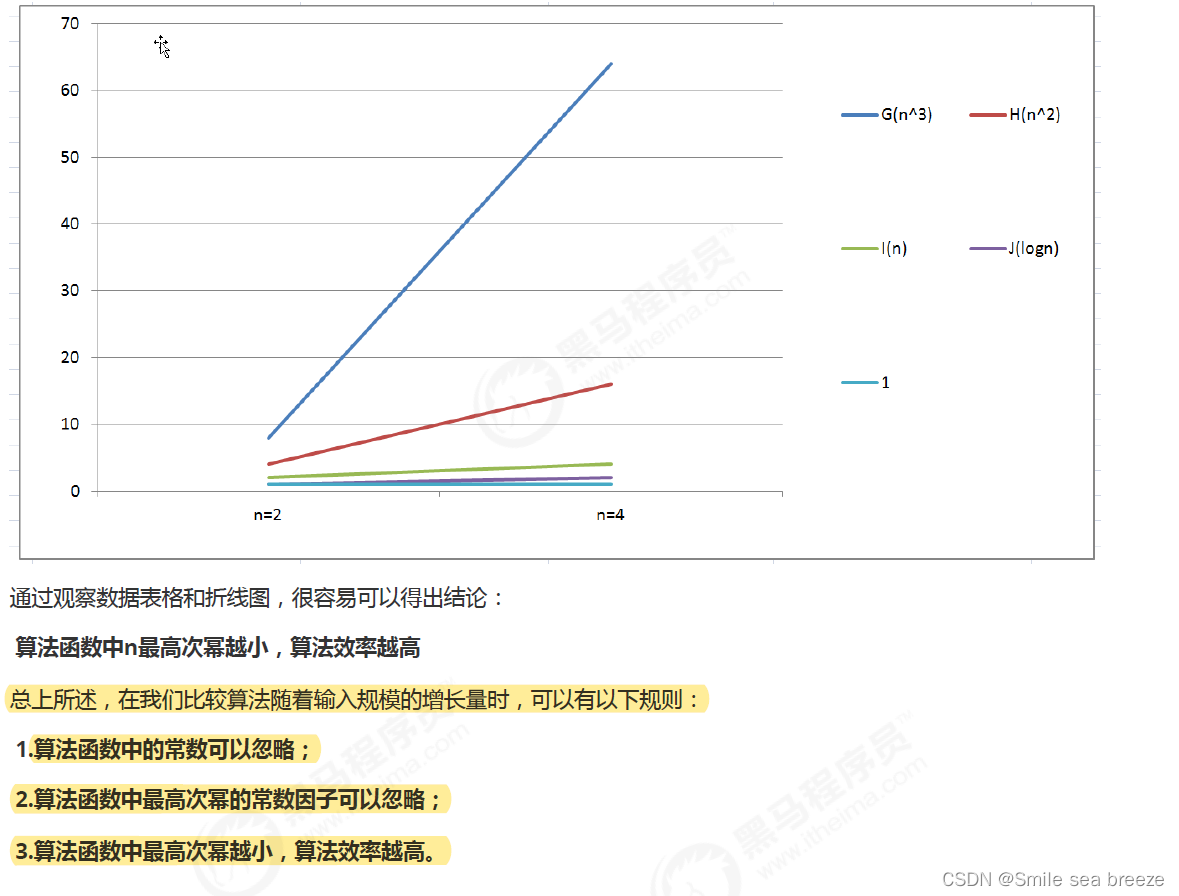
1.2 算法的时间复杂度

定义：

在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随着n的变化情况并确定T(n)的
量级。算法的时间复杂度，就是算法的时间量度，记作:T(n)=O(f(n))。它表示随着问题规模n的增大，算法执行时间
的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称时间复杂度，其中f(n)是问题规模n的某个函数。
在这里，我们需要明确一个事情：执行次数=执行时间

用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。一般情况下，随着输入规模n的增大，T(n)增长最
慢的算法为最优算法。
下面我们使用大O表示法来表示一些求和算法的时间复杂度：

1.3常见的大O阶

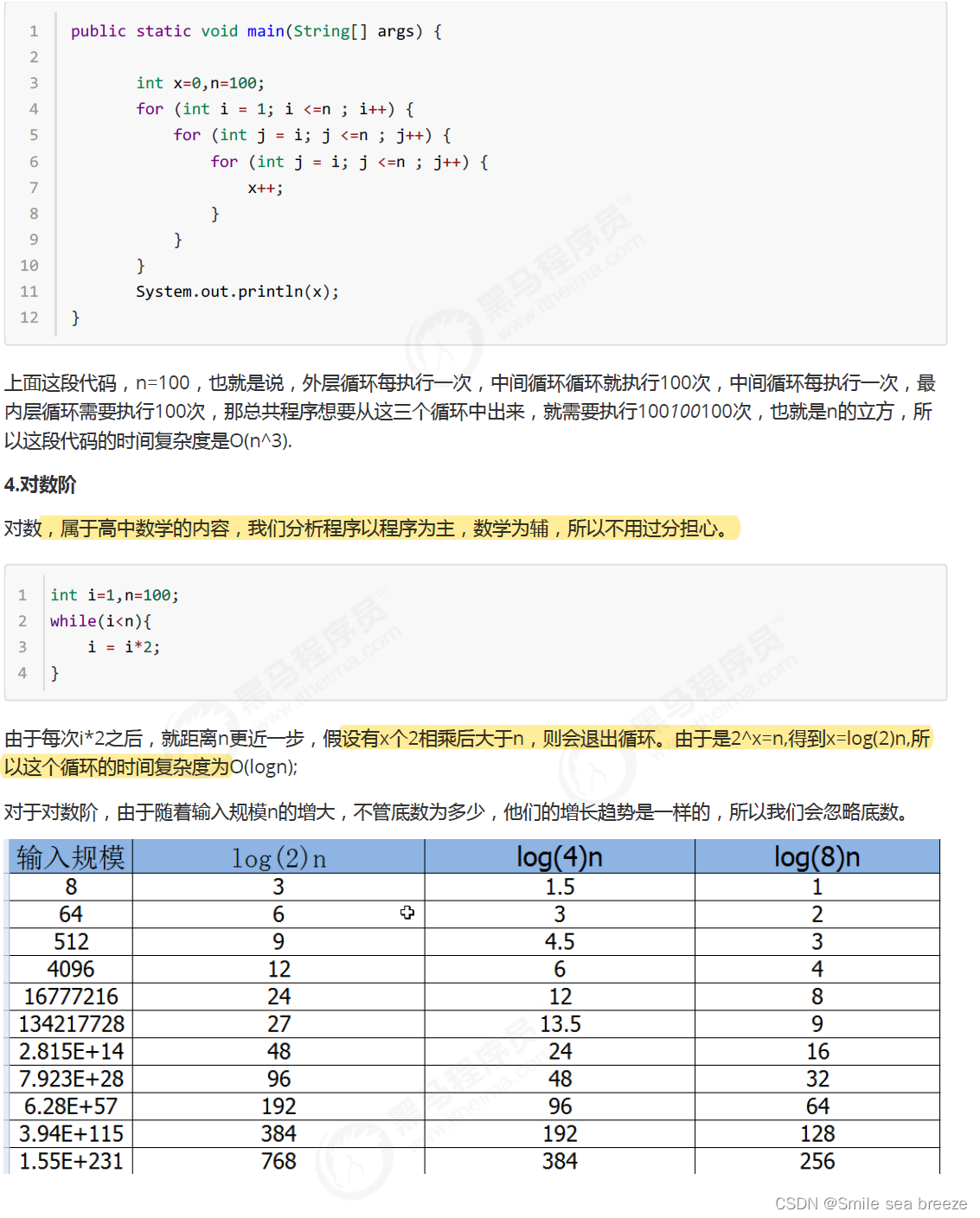
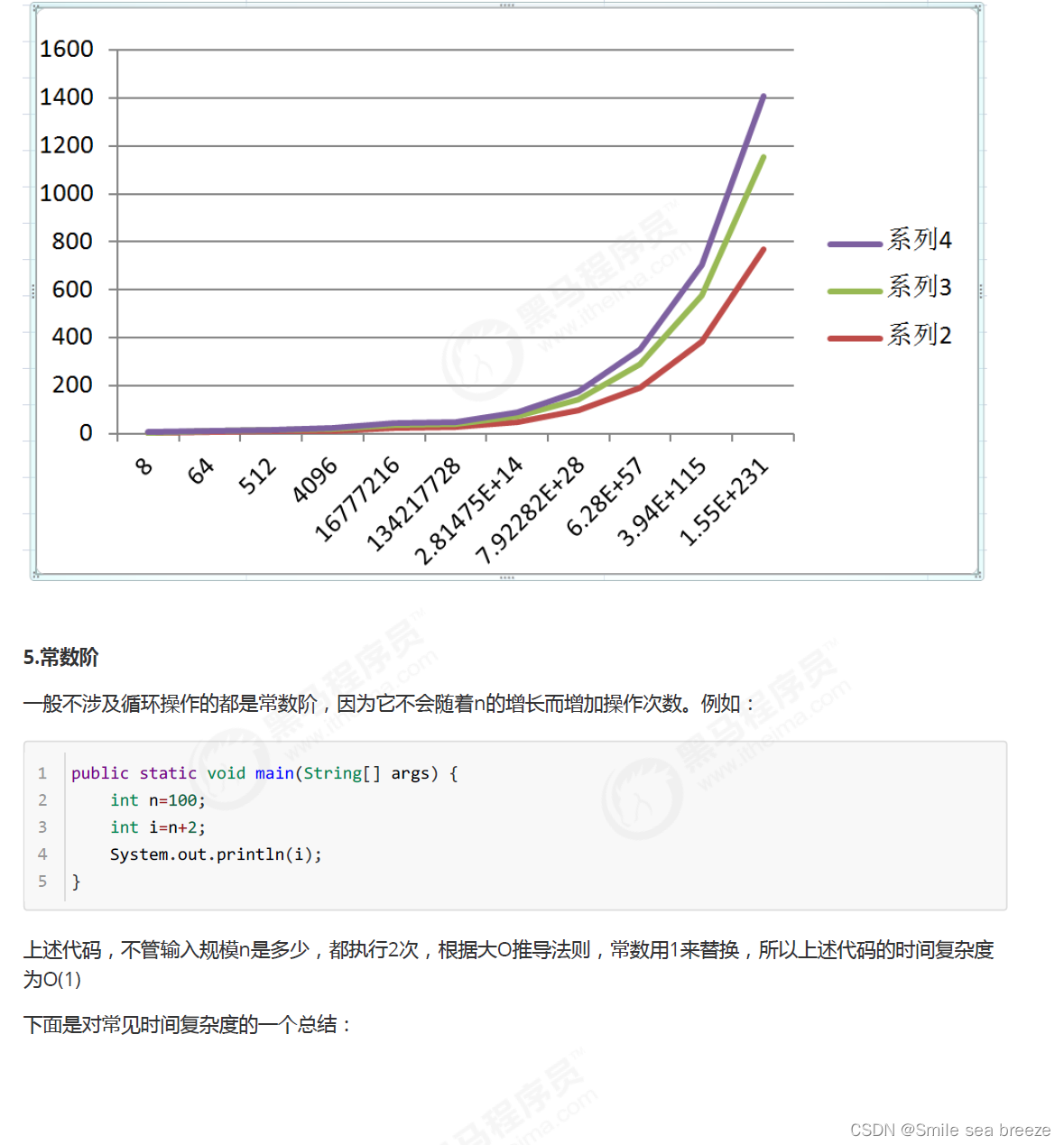
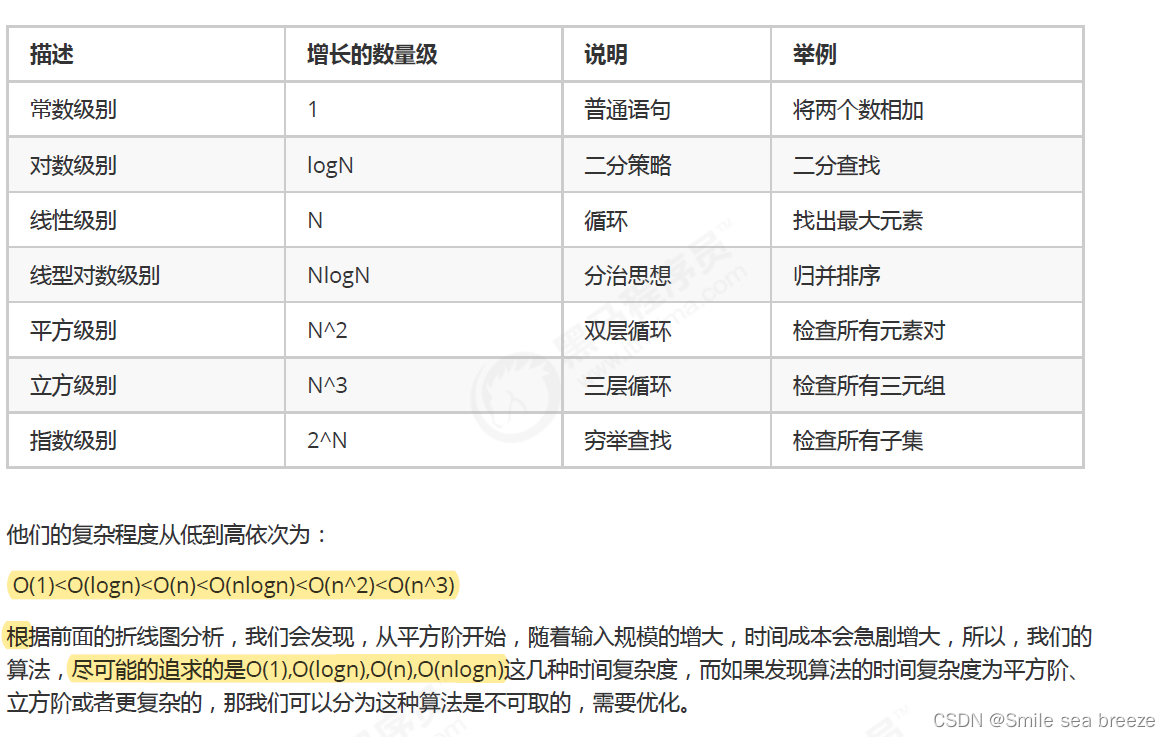
1.4 函数调用的时间复杂度分析

1.4.1最坏情况

例：

public int search(int num){
int[] arr={11,10,8,9,7,22,23,0};
for (int i = 0; i < arr.length; i++) {
if (num==arr[i]){
return i;
}
}
return -1;
}

最好情况：
查找的第一个数字就是期望的数字，那么算法的时间复杂度为O(1)
最坏情况：
查找的最后一个数字，才是期望的数字，那么算法的时间复杂度为O(n)
平均情况：
任何数字查找的平均成本是O(n/2)
最坏情况是一种保证，在应用中，这是一种最基本的保障，即使在最坏情况下，也能够正常提供服务，所以，除非特别指定，我们提到的运行时间都指的是最坏情况下的运行时间。

1.5 空间复杂度分析

算法的空间复杂度计算公式记作：S(n)=O(f(n)),其中n为输入规模，f(n)为语句关于n所占存储空间的函数。

案例：
对指定的数组元素进行反转，并返回反转的内容。

解法一：

public static int[] reverse1(int[] arr){
int n=arr.length;//申请4个字节
int temp;//申请4个字节
for(int start=0,end=n-1;start<=end;start++,end--){
temp=arr[start];
arr[start]=arr[end];
arr[end]=temp;
}
return arr;
}

解法二：

public static int[] reverse2(int[] arr){
int n=arr.length;//申请4个字节
int[] temp=new int[n];//申请n*4个字节+数组自身头信息开销24个字节
for (int i = n-1; i >=0; i--) {
temp[n-1-i]=arr[i];
}
return temp;
}

忽略判断条件占用的内存，我们得出的内存占用情况如下：
算法一：
不管传入的数组大小为多少，始终额外申请4+4=8个字节；
算法二：
4+4n+24=4n+28;
根据大O推导法则，算法一的空间复杂度为O(1),算法二的空间复杂度为O(n),所以从空间占用的角度讲，算法一要优于算法二。
由于java中有内存垃圾回收机制，并且jvm对程序的内存占用也有优化（例如即时编译），我们无法精确的评估一个java程序的内存占用情况，但是了解了java的基本内存占用，使我们可以对java程序的内存占用情况进行估算。
由于现在的计算机设备内存一般都比较大，基本上个人计算机都是4G起步，大的可以达到32G，所以内存占用一般情况下并不是我们算法的瓶颈，普通情况下直接说复杂度，默认为算法的时间复杂度。