[NOI2019] 斗主地
题目背景
时限 4 秒 内存 512MB
题目描述
小 S 在和小 F 玩一个叫“斗地主”的游戏。
可怜的小 S 发现自己打牌并打不过小 F,所以他想要在洗牌环节动动手脚。
一副牌一共有 n n n 张牌,从上到下依次标号为 1 ∼ n 1 \sim n 1∼n。标号为 i i i 的牌分数是 f ( i ) f(i) f(i)。在本题, f ( i ) f(i) f(i) 有且仅有两种可能: f ( i ) = i f(i) = i f(i)=i 或 f ( i ) = i 2 f(i) = i^2 f(i)=i2。
洗牌的方式和我们日常生活中的比较类似,以下我们用形式化的语言来定义: 洗牌环节一共分 m m m 轮,这 m m m 轮洗牌依次进行。第 i i i 轮洗牌时:
- 小 S 会拿出从最上面往下数的前 A i A_i Ai 张牌。这样这副牌就被分成了两堆:第一堆 是最上面的 A i A_i Ai 张牌,第二堆是剩下的 n − A i n-A_i n−Ai 张牌,且这两堆牌内相对顺序不变。 特别地,当 A i = n A_i = n Ai=n 或 A i = 0 A_i = 0 Ai=0 时,有一堆牌是空的。
- 接下来对两堆牌进行合并,从而产生新的第三堆牌。当第一堆牌还剩下 X X X 张,第二堆牌还剩下 Y Y Y 张的时候,以 X X + Y \dfrac{X}{X+Y} X+YX 的概率取出第一堆牌的最下面的牌,并将它 放入新的第三堆牌的最上面, Y X + Y \dfrac{Y}{X+Y} X+YY 的概率取出第二堆牌的最下面的牌,并将它放入新的第三堆牌的最上面
- 重复操作 2 2 2,一直取到两堆牌都为空为止。这样我们就完成了一轮洗牌。
因为洗牌过程是随机的,所以小 S 发现自己没法知道某个位置上具体是哪张牌。但小 S 想问你在经历了这 m m m 轮洗牌后,某个位置上的牌的期望分数是多少。小 S 一共会问你 Q Q Q 个这样的问题。
输入格式
输入的第一行包含三个正整数 n , m , t y p e n, m, type n,m,type,分别表示牌的数量,洗牌的轮数与 f ( i ) f(i) f(i) 的类型。当 t y p e = 1 type = 1 type=1 时, f ( i ) = i f(i) = i f(i)=i。当 t y p e = 2 type = 2 type=2 时, f ( i ) = i 2 f(i) = i^2 f(i)=i2。
接下来一行,一共 m m m 个整数,表示 A 1 ∼ A m A_1 \sim A_m A1∼Am。
接下来一行一个正整数 Q Q Q,表示小 S 的询问个数。 接下来 Q Q Q 行,每行一个正整数 c i c_i ci,表示小 S 想要知道从上往下第 c i c_i ci 个位置上的牌的期望分数。
保证 1 ≤ c i ≤ n 1 \leq c_i \leq n 1≤ci≤n。
输出格式
输出一共 Q Q Q 行,每行一个整数,表示答案在模 998244353 998244353 998244353 意义下的取值。
即设答案化为最简分式后的形式为 a b \dfrac{a} {b} ba,其中 a a a 和 b b b 互质。输出整数 x x x 使得 b x ≡ a ( m o d 998244353 ) bx \equiv a \pmod{998244353} bx≡a(mod998244353) 且 0 ≤ x < 998244353 0 ≤ x < 998244353 0≤x<998244353。可以证明这样的整数 x x x 是唯一的。
样例 #1
样例输入 #1
4 1 1
3
1
1
样例输出 #1
249561090
提示
更多样例
您可以通过附加文件获得更多样例。
样例 2
见附加文件中的 landlords/landlords2.in 与 landlords/landlords2.ans。
样例 3
见附加文件中的 landlords/landlords3.in 与 landlords/landlords3.ans。
样例输入输出 1 解释
- 有 1 4 \dfrac{1}{4} 41 的概率从上到下的最终结果是 { 1 , 2 , 3 , 4 } \{1, 2, 3, 4\} {1,2,3,4}。
- 有 1 4 \dfrac{1}{4} 41 的概率从上到下的最终结果是 { 1 , 2 , 4 , 3 } \{1, 2, 4, 3\} {1,2,4,3}。
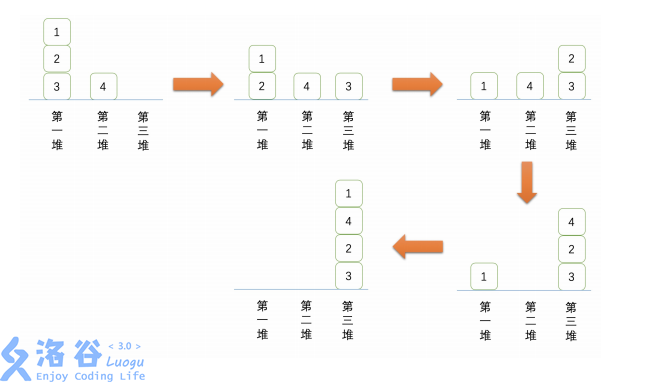
- 有 1 4 \dfrac{1}{4} 41 的概率从上到下的最终结果是 { 1 , 4 , 2 , 3 } \{1, 4, 2, 3\} {1,4,2,3}。
- 有 1 4 \dfrac{1}{4} 41 的概率从上到下的最终结果是 { 4 , 1 , 2 , 3 } \{4, 1, 2, 3\} {4,1,2,3}。
所以最终有 1 4 \dfrac{1}{4} 41 的概率第一个位置是 4 4 4,有 3 4 \dfrac{3} {4} 43 的概率第一个位置是 1 1 1,所以第一个位置的期望分数是 7 4 \dfrac{7}{ 4} 47。
为了帮助你们更直观地了解洗牌的过程,我们在下面画出了结果是 { 1 , 4 , 2 , 3 } \{1, 4, 2, 3\} {1,4,2,3} 的过程。
数据规模与约定
对于全部的测试点,保证 3 ≤ n ≤ 1 0 7 3\le n \le 10^7 3≤n≤107, 1 ≤ m , Q ≤ 5 × 1 0 5 1\le m,Q\le5\times 10^5 1≤m,Q≤5×105, 0 ≤ A i ≤ n 0\le A_i\le n 0≤Ai≤n, t y p e ∈ { 1 , 2 } type\in \{1,2\} type∈{1,2}。
每个测试点的具体限制见下表:
| 测试点 | n n n | m m m | t y p e = type= type= | 其他性质 |
|---|---|---|---|---|
| 1 1 1 | ≤ 10 \le 10 ≤10 | ≤ 1 \le 1 ≤1 | 1 1 1 | 无 |
| 2 2 2 | ≤ 80 \le 80 ≤80 | ≤ 80 \le 80 ≤80 | 1 1 1 | 无 |
| 3 3 3 | ≤ 80 \le 80 ≤80 | ≤ 80 \le 80 ≤80 | 2 2 2 | 无 |
| 4 4 4 | ≤ 100 \le 100 ≤100 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 2 2 2 | 所有 A i A_i Ai 相同 |
| 5 5 5 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 1 1 1 | 无 |
| 6 6 6 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 1 1 1 | 无 |
| 7 7 7 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 1 1 1 | 无 |
| 8 8 8 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 2 2 2 | 无 |
| 9 9 9 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 2 2 2 | 无 |
| 10 10 10 | ≤ 1 0 7 \le 10^7 ≤107 | ≤ 5 × 1 0 5 \le 5\times 10^5 ≤5×105 | 2 2 2 | 无 |
请注意我们并没有保证 Q ≤ n Q\le n Q≤n。
提示
这里我们给出离散型随机变量 X X X 的期望 E [ x ] \mathbb{E}[x] E[x] 的定义:
设离散随机变量
X
X
X 的可能值是
X
1
,
X
2
,
…
X
k
X_1,X_2,\ldots X_k
X1,X2,…Xk,
P
r
[
X
1
]
,
P
r
[
X
2
]
,
…
,
P
r
[
X
k
]
Pr[X_1],Pr[X_2],\ldots,Pr[X_k]
Pr[X1],Pr[X2],…,Pr[Xk] 为
X
X
X 取对应值的概率,则
X
X
X 的期望为:
E
[
x
]
=
∑
i
=
1
k
X
i
×
P
r
[
X
i
]
\mathbb{E}[x]=\sum^k_{i=1}X_i\times Pr[X_i]
E[x]=i=1∑kXi×Pr[Xi]
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int kcz=998244353;
const int maxn=10000005;
ll a,b,c,f[maxn];
int n;
inline ll qpow(ll a,ll k)
{
ll res=1;
while(k)
{
if(k&1) res=res*a%kcz;
if(k>>=1) a=a*a%kcz;
}
return res;
}
inline ll calc(ll x) { return ((a*x+b)%kcz*x+c)%kcz; } // 算第x个数的期望
int main()
{
int m,tp,i;
ll _,__,t1,t2,t3,t,___,sqn;
freopen("landlords.in","r",stdin),freopen("landlords.out","w",stdout);
scanf("%d%d%d",&n,&m,&tp),sqn=n*(ll)n%kcz;
_=qpow(n-1,kcz-2),__=qpow(n,kcz-2),___=qpow((-sqn+3*n-2)%kcz,kcz-2);
if(tp==1) a=c=0,b=1;
else a=1,b=c=0; // x_i=ai^2+bi+c
while(m--)
{
scanf("%lld",&t);
if(t==0 || t==n) continue;
t1=(calc(1)*t+calc(t+1)*(n-t))%kcz*__%kcz; // 第一个
t2=((calc(2)*(t-1)+calc(t+1)*(n-t))%kcz*t+(calc(1)*t+calc(t+2)*(n-t-1))%kcz*(n-t))%kcz*__%kcz*_%kcz; // 第二个
t3=(calc(t)*t+calc(n)*(n-t))%kcz*__%kcz; // 第n个
a=((2-n)*t1+(n-1)*t2-t3)%kcz*___%kcz;
b=((sqn-4)*t1+(1-sqn)*t2+3*t3)%kcz*___%kcz;
c=((4*n-2*sqn)*t1+(sqn-n)*t2-2*t3)%kcz*___%kcz; // 极其丑的差值
}
for(i=1;i<=n;i++)
f[i]=(calc(i)+kcz)%kcz;
scanf("%d",&m);
while(m--)
scanf("%lld",&t),printf("%lld\n",f[t]);
fclose(stdin),fclose(stdout);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int kcz=998244353;
const int maxn=10000005;
ll a,b,c,a_,b_,c_,fac[maxn],inv[maxn],inv_fac[maxn];
int n;
inline ll f(ll x) { return (a+b*(x-1)+c*(x-1)%kcz*(x-2))%kcz; } // 算第x个数的期望
inline ll C(int n,int m) { return (m>=0 && m<=n)?fac[n]*inv_fac[m]%kcz*inv_fac[n-m]%kcz:0; } // 判一下0的情况
inline ll invC(int n,int m) { return inv_fac[n]*fac[m]%kcz*fac[n-m]%kcz; }
int main()
{
int i,q,op,A;
ll t;
freopen("landlords.in","r",stdin),freopen("landlords.out","w",stdout);
scanf("%d%d%d",&n,&q,&op);
if(op==1) a=b=1,c=0; // a_i=a+b*(i-1)+c*(i-1)*(i-2)
else a=1,b=3,c=1;
fac[0]=inv_fac[0]=inv[1]=fac[1]=inv_fac[1]=1;
for(i=2;i<=n;i++)
{
fac[i]=fac[i-1]*i%kcz;
inv[i]=-(kcz/i)*inv[kcz%i]%kcz;
inv_fac[i]=inv_fac[i-1]*inv[i]%kcz;
}
while(q--)
{
scanf("%d",&A);
a_=(a+b*A+c*A%kcz*(A-1ll))%kcz; // 平移x->x+A
b_=(b+c*2*A)%kcz;
c_=c;
t=invC(n,A);
a=(a*C(n-1,A-1)+a_*C(n-1,n-A-1))%kcz*t%kcz; // 更新系数
b=(b*C(n-2,A-2)+b_*C(n-2,n-A-2))%kcz*t%kcz;
c=(c*C(n-3,A-3)+c_*C(n-3,n-A-3))%kcz*t%kcz;
}
scanf("%d",&q);
while(q--)
scanf("%d",&i),printf("%lld\n",(f(i)+kcz)%kcz);
fclose(stdin),fclose(stdout);
return 0;
}
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=500000+10;
const int maxm=10000000+10;
const int mod=998244353;
const int inv2=(mod+1)>>1;
int n,m,q,type;ll A,B,C,f[10][10],g[10],h[10],w[10],inv[maxm];
inline ll F(int x) {return (A*x%mod*x+B*x+C)%mod;}
int main()
{
scanf("%d%d%d",&n,&m,&type);
inv[0]=inv[1]=1;
for(int i=2;i<=n;i++) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
if(type==1) A=0,B=1,C=0;
else A=1,B=0,C=0;
int tmp;ll X,Y,Z;
for(int i=1;i<=m;i++)
{
scanf("%d",&tmp);
for(int j=1;j<=3;j++) g[j]=F(j),h[j]=F(j+tmp),w[j]=0;
for(int j=0;j<3;j++)
for(int k=0;k<3;k++) f[j][k]=0;
f[0][0]=1;
for(int j=0;j<3;j++)
for(int k=0;k<3;k++)
{
if(j+k>=3) break;
if(j<tmp)
{
ll val=f[j][k]*(tmp-j)%mod*inv[n-j-k]%mod;
(f[j+1][k]+=val)%=mod;
(w[j+k+1]+=val*g[j+1])%=mod;
}
if(k<n-tmp)
{
ll val=f[j][k]*(n-tmp-k)%mod*inv[n-j-k]%mod;
(f[j][k+1]+=val)%=mod;
(w[j+k+1]+=val*h[k+1])%=mod;
}
}
X=w[1];Y=w[2];Z=w[3];
A=((Z-2*Y+X)*inv2%mod+mod)%mod;
B=((8*Y-5*X-3*Z)*inv2%mod+mod)%mod;
C=((3*X-3*Y+Z)%mod+mod)%mod;
}
scanf("%d",&q);
while(q--)
{
scanf("%d",&tmp);
printf("%lld\n",F(tmp));
}
return 0;
}