01背包

题目链接：01背包

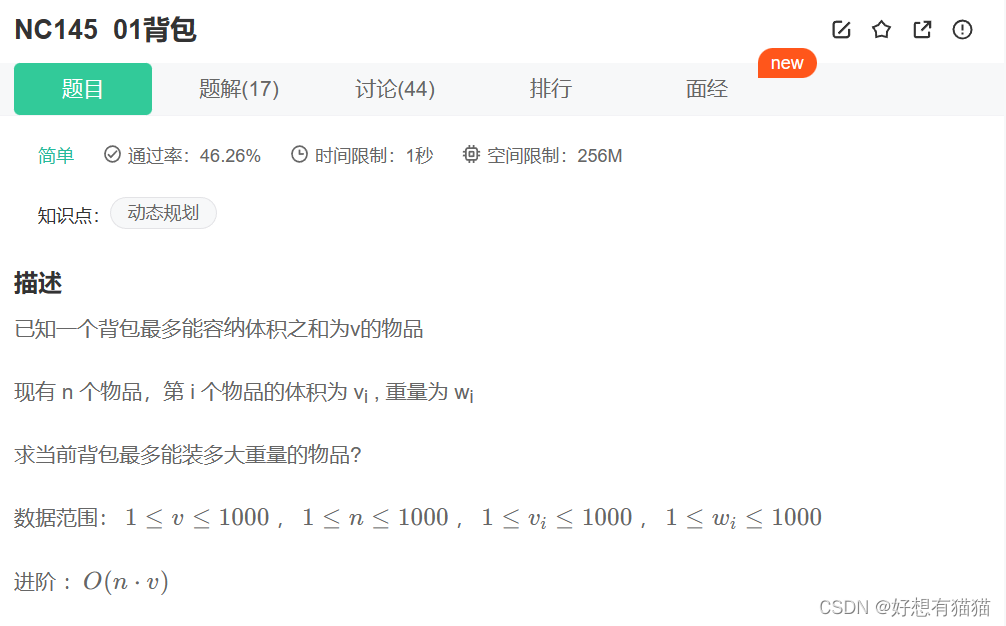
思路：题目要求是获取背包能装的最大重量。一个物品有体积和重量两个属性。而当我们判断一个物品是否要放进背包，第一取决于他的体积是否足以放进背包，第二取决于他的重量是否足以让我们取出已经放入的一部分物品，再放入该物品。所以我们要保存放入该物品之前的状态，于是我们想到可以使用动态规划。

---

因为物品有两个属性，我们可以使用二维数组F（i，j）记录。
状态：F(i，j)：前i个物品放入大小为j的背包中获得的最大重量（将体积为V的背包分治成1~V大小的背包）
状态转移方程：
对于第i个物品，和1~V的体积的背包，有两种情况：

1. 当前j体积的背包不足以放入第i个物品，那么F(i，j)=F(i-1，j)，即不放入
2. 当前j体积的背包可以放入第i个物品，那么此时有两个选择，放与不放

放：需要腾出足够的空间放入，F(i，j)=F(i-1，j - vw[i][0])+vw[i][1]
PS：j - vw[i][0]代表腾出足够空间，+vw[i][1]代表放入该物品，要加上重量

不放：F(i，j)=F(i-1，j)

最后取两个选择中，重量较大的那个
F(i,j)=max(F(i-1，j - vw[i][0]) + vw[i][1]，F(i-1，j) )

图片来自牛客题解：摸鱼学大师

第0行和第0列初始化为1

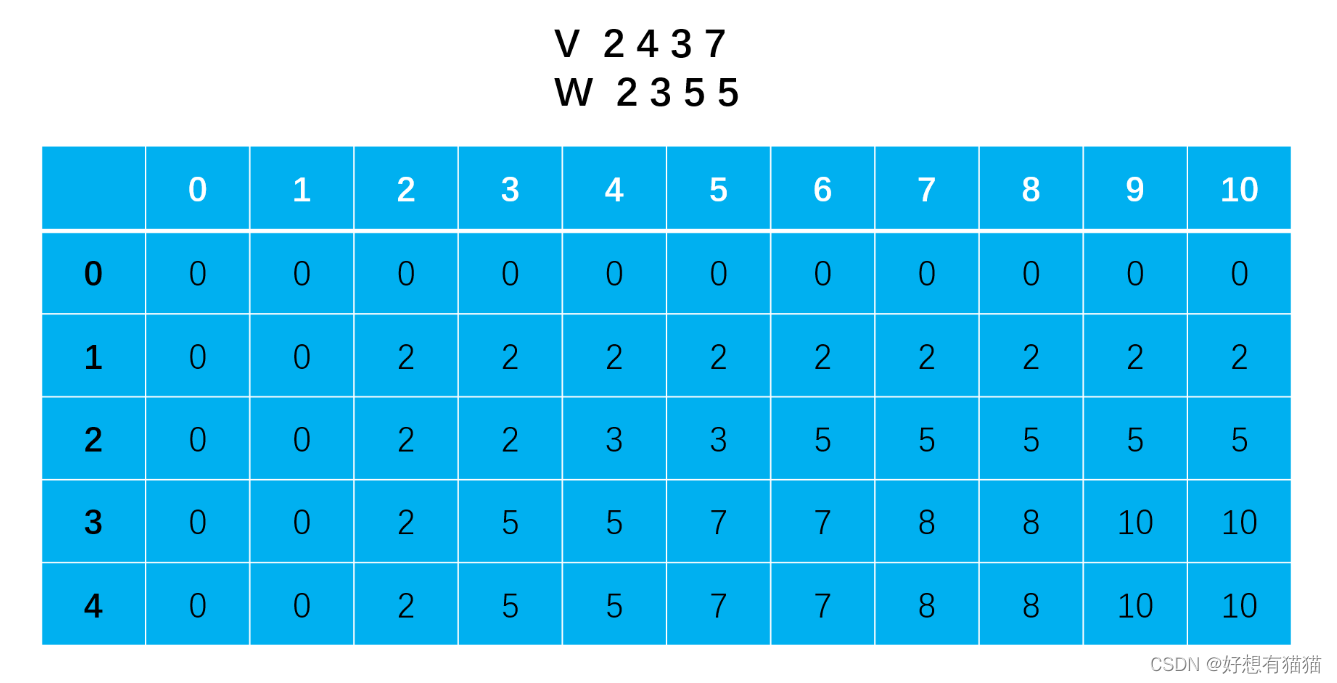
代码如下：

int knapsack(int V, int n, vector<vector<int> >& vw)
{
    vector<vector<int>> dp(n+1,vector<int>(V+1,0));
    //i和j都从1开始访问，并且要访问到最后一个商品和背包的最大容量
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=V;++j)
        {
            //容量足够
            //i=1代表第一个商品，但对于vw的第0行
            if(vw[i-1][0]<=j)
               dp[i][j]=max(dp[i-1][j],dp[i-1][j-vw[i-1][0]]+vw[i-1][1]);
            else
               dp[i][j]=dp[i-1][j];
        }
    }

    return dp[n][V];
}

在实际运行过程中，我们发现，二维数组其实每次只会用到当前行的上一行，所以我们可以用一维数组代替。
但是在递推时，更新应该从右往左，才不会提前覆盖上一行的数据

int knapsack(int V, int n, vector<vector<int> >& vw) {
        //一维数组
        //因为每次更新只需要用到上一行
        //所以我们可以使用一维数组记录上一行，然后从右往左更新
        vector<int> dp(V+1,0);

        for(int i=1;i<=n;++i)
        {
            for(int j=V;j>0;--j)
            {
                if(vw[i-1][0]<=j)
                    dp[j]=max(dp[j],dp[j-vw[i-1][0]]+vw[i-1][1]);
            }
        }

        return dp[V];
    }