构造哈夫曼树:
先带权值最小的,再找有关系的(一般是相等或相近),没关系的放一边,最后将有关系的和没关系的组成一个哈夫曼树。
.
最小生成树:
顶点数:n
边数:n-1
kruskal:找最小边
prim:从一个点出发,根据点的集合找最小边
.
深度、高度不包括叶子节点
区别:
深度指的是从根节点到某个节点的路径长度,而高度指的是从某个节点到最远叶子节点的路径长度。
相关例题:
一个高度为5的3阶B树还有的关键字个数至少是:
2**5-1=31
.
小根堆:每个小三角形内都是三数最小的当根
大根堆:每个小三角形内都是三数最大的当根
调整过程都是自底向上进行的。
.
平衡二叉树:
计算时左减右
- LL型:
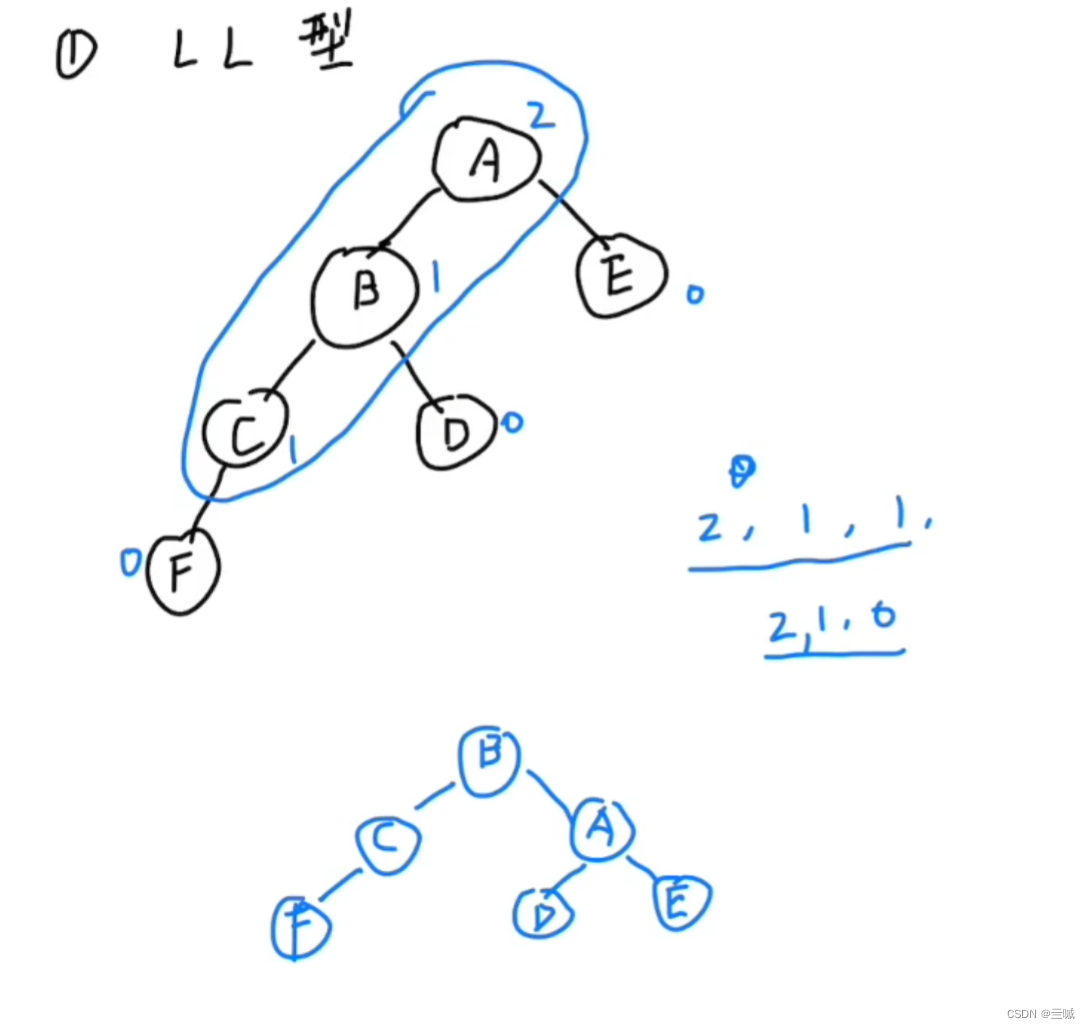
- RR型:

下面C换成D - LR型:
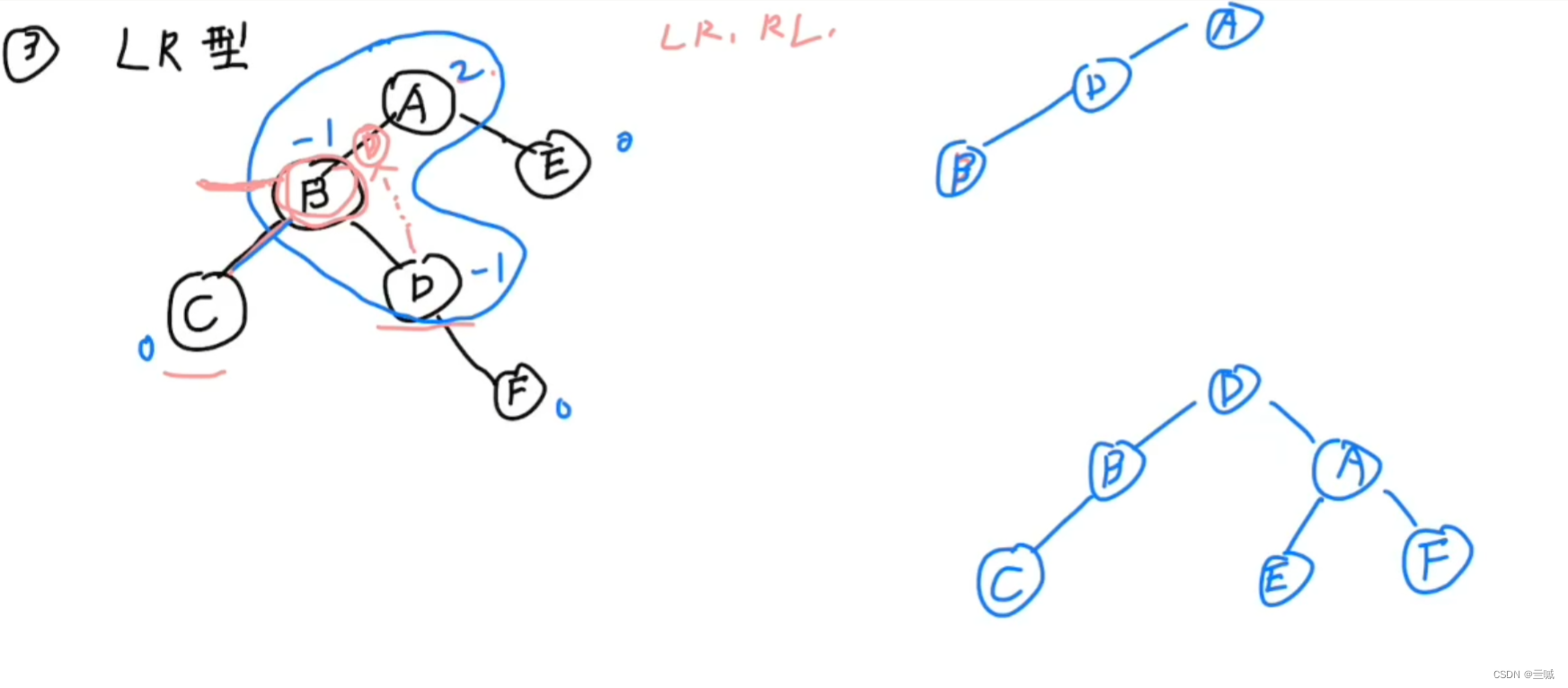
E、F互换 - RL型:
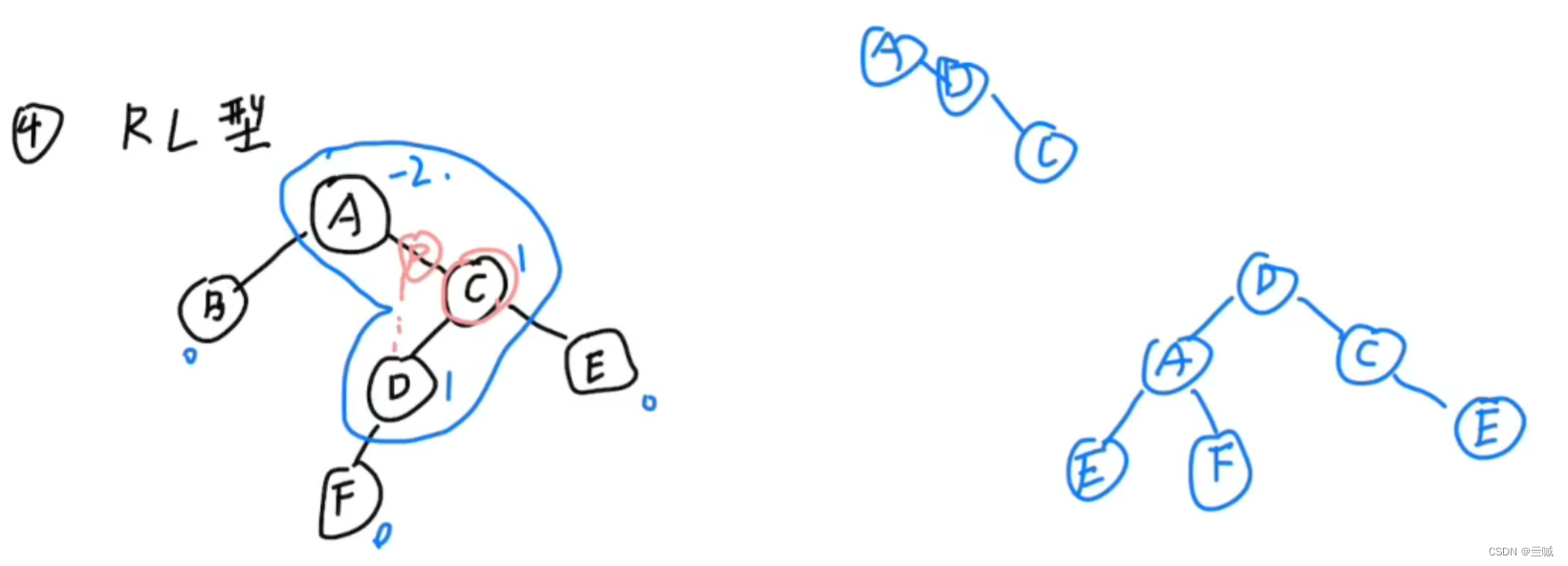
左边的E应该是B
.
对 m 个初始归并段进行 k -路平衡归并:
(读的次数+写的次数)*趟数+内部排序(读的次数+写的次数)
趟数= log 以 k 为底 m 的对数,进行向上取整
为实现最佳归并,需要补充的虚段(长度为 0 的初始归并段)个数:
公式:( m - 1 )%( k - 1 )
当公式的值为 0 时,不用补
当公式的值不为 0 时,需要补充的虚段个数为:k -公式- 1
读写外存次数最少的归并方案:
在初始归并段最开头添加需要补充的虚段个数个 0 ,形成哈夫曼树,
此时的哈夫曼树是 k 叉树。
此时读写外存次数:哈夫曼树的带权值 * 2
.
Dijkstra:按点的集合找最小边形成最短路径
Prim:直接找最小边,按边找最短路径
.
线索二叉树:
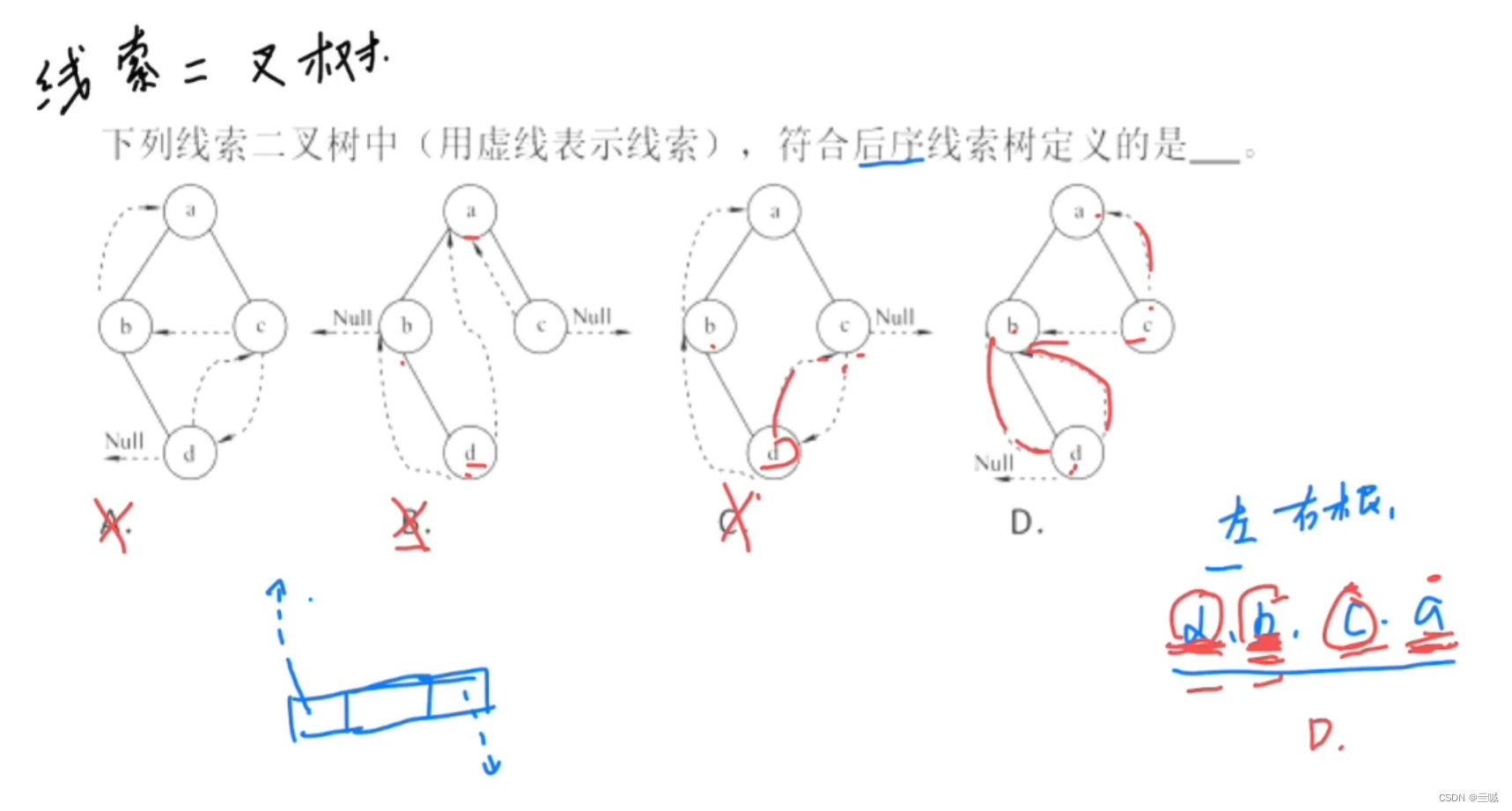
先按画图法或三角形法列出遍历序列,必须挨着才能连线。
.
对一个树来说:出度 = 入度
总结点个数 = 入度个数 + 1(根无入度)
一个度为 n 的树中,每个结点最多可以有 n 个子结点。
.
拓扑序列:每次找没有入度的点
.
快速排序:
- 第一趟:先在最右侧设一个哨兵,在最左侧设置 Left,在除哨兵之外最右侧设置 Right。Left 找大于哨兵的数,找到之后不动,等待 Right 找小于哨兵的数,找到后两数交换。当 Left 和 Right 重合时,判断 Left 和 Right 指向的数和哨兵的大小关系,进而判断是否要交换两数。
- 第二趟:在中间位置设哨兵,重复上述操作。(左半部分)
- 第三趟:(右半部分)
- 继续上述操作,直到排序完成
.
循环队列:
- front = rear 时,队列为空或队满
- 循环队列 A [0] 不一定是第一个元素所在位置,同样,front 和 rear 的位置是不固定的,不一定指向 A [0]
- 添加元素后,rear 指针向后移动;添加元素前,rear 在上一个位置。
.
哈希表处理冲突的方式:
都是哈希法存数:
- 线性探测

- 二次探测
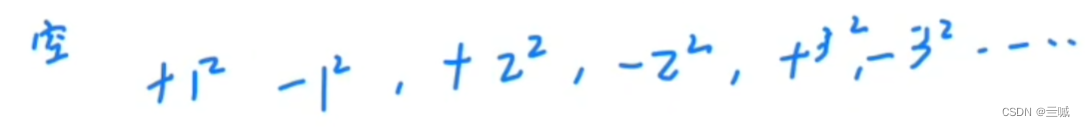
- 链接法
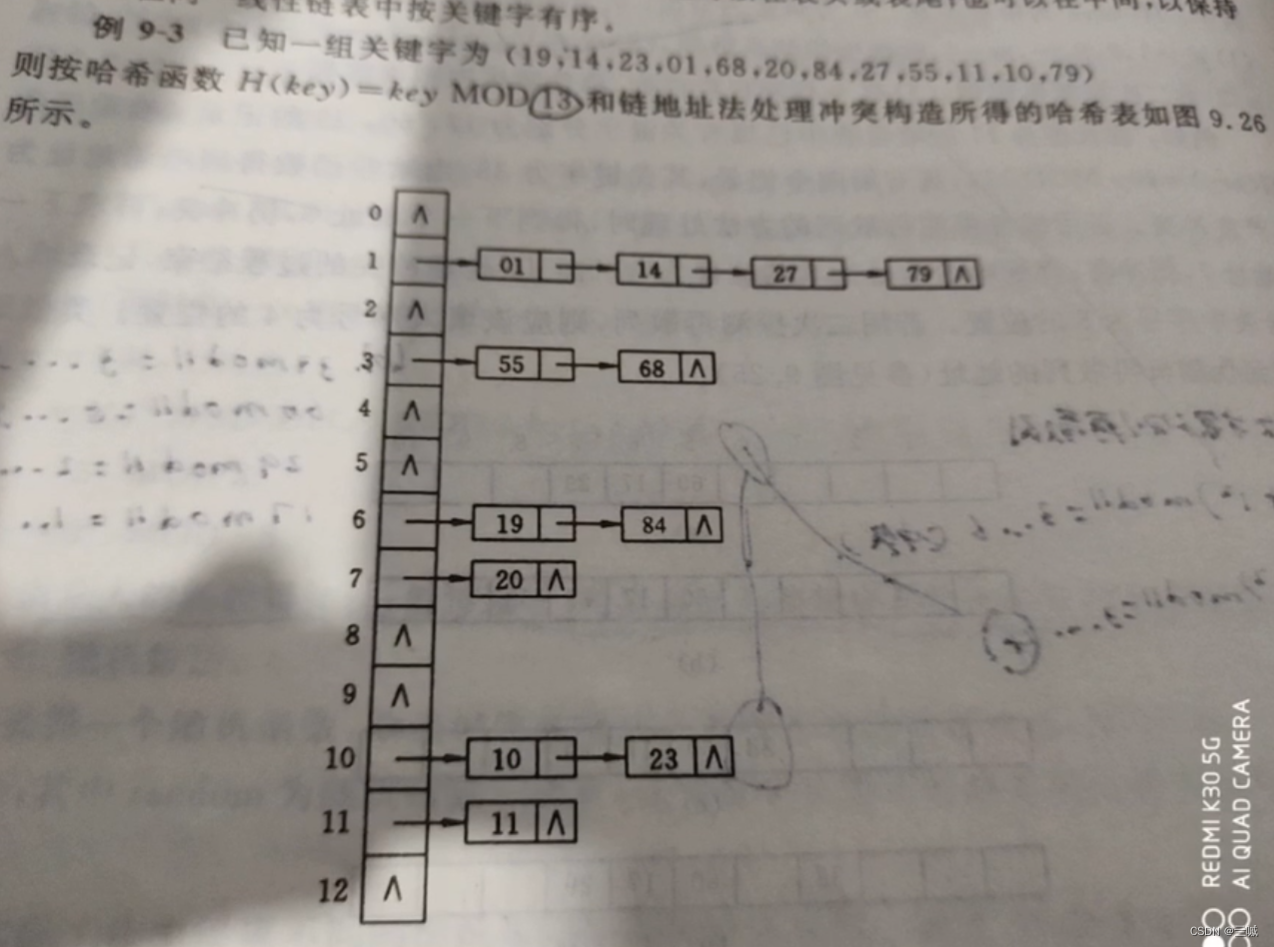
.
稀疏矩阵:
- 三元组线性表:(所有非零元素的( 行,列,值 ))
- 十字链表
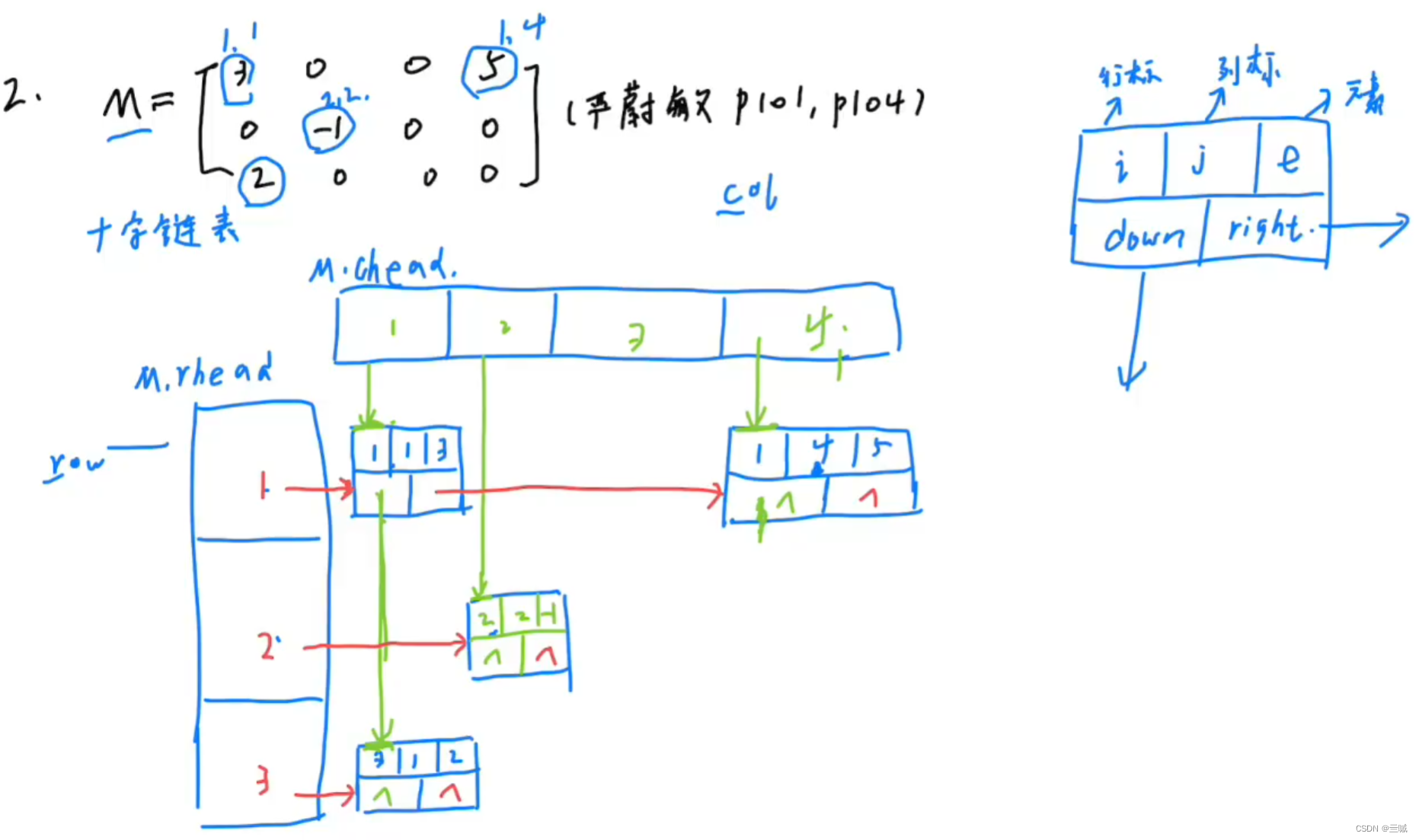
.
广义表:
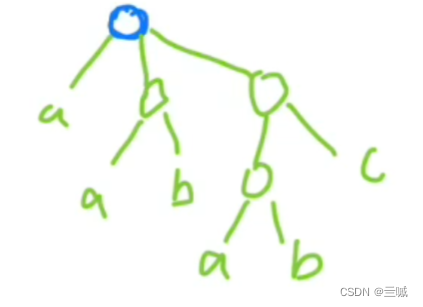
表头是第一个元素
表尾是除第一个元素之外的其他所有元素
.
关键路径:
- 最早开始时间 = 最晚开始时间的结点连起来 且 权值相加 = 正推结束后的值
- 最早开始时间 = Max( n1,n2) 正推
- 最晚开始时间 = Min( n1,n2 ) 逆推
- 起点和终点最早开始时间 = 最晚开始时间
- 起点为( 0,0 )终点为为正推结束后的值
例子:
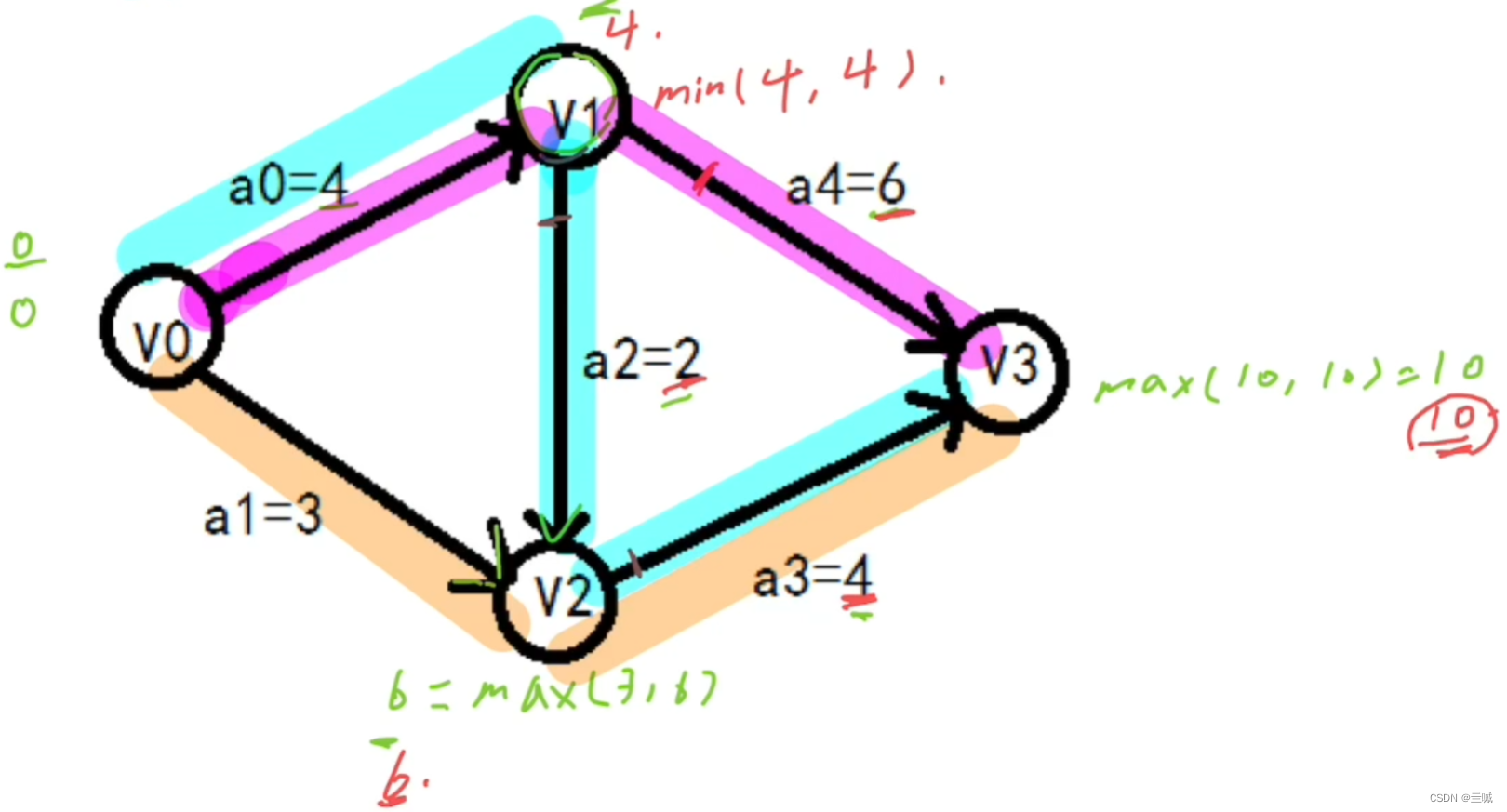
.
深度优先和广度优先生成树:
深度优先:
案例:
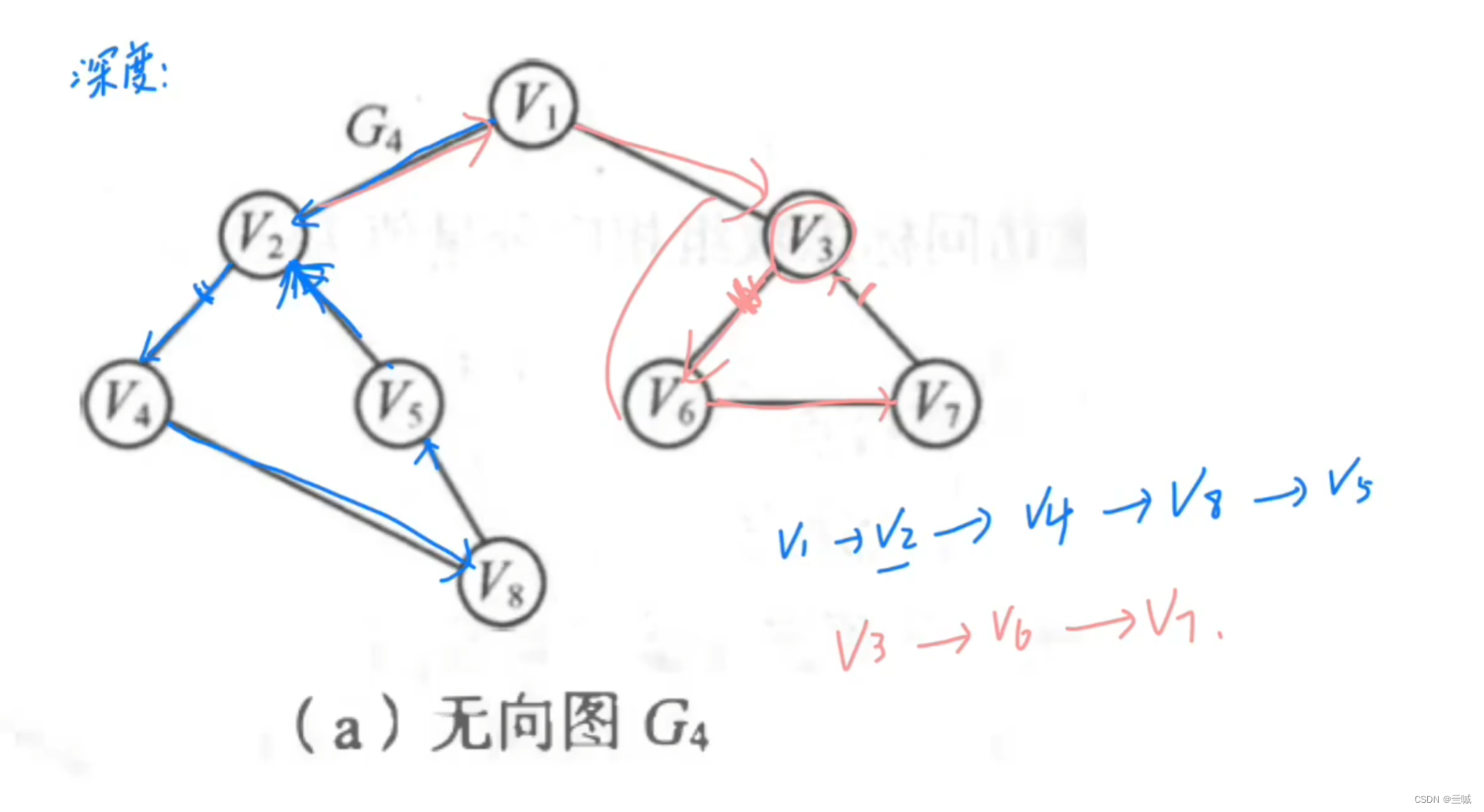
广度优先:
- 类似层次遍历
- 任何结点都可以成为顶点,与顶点相连的是第二层,同理依次向下
案例:
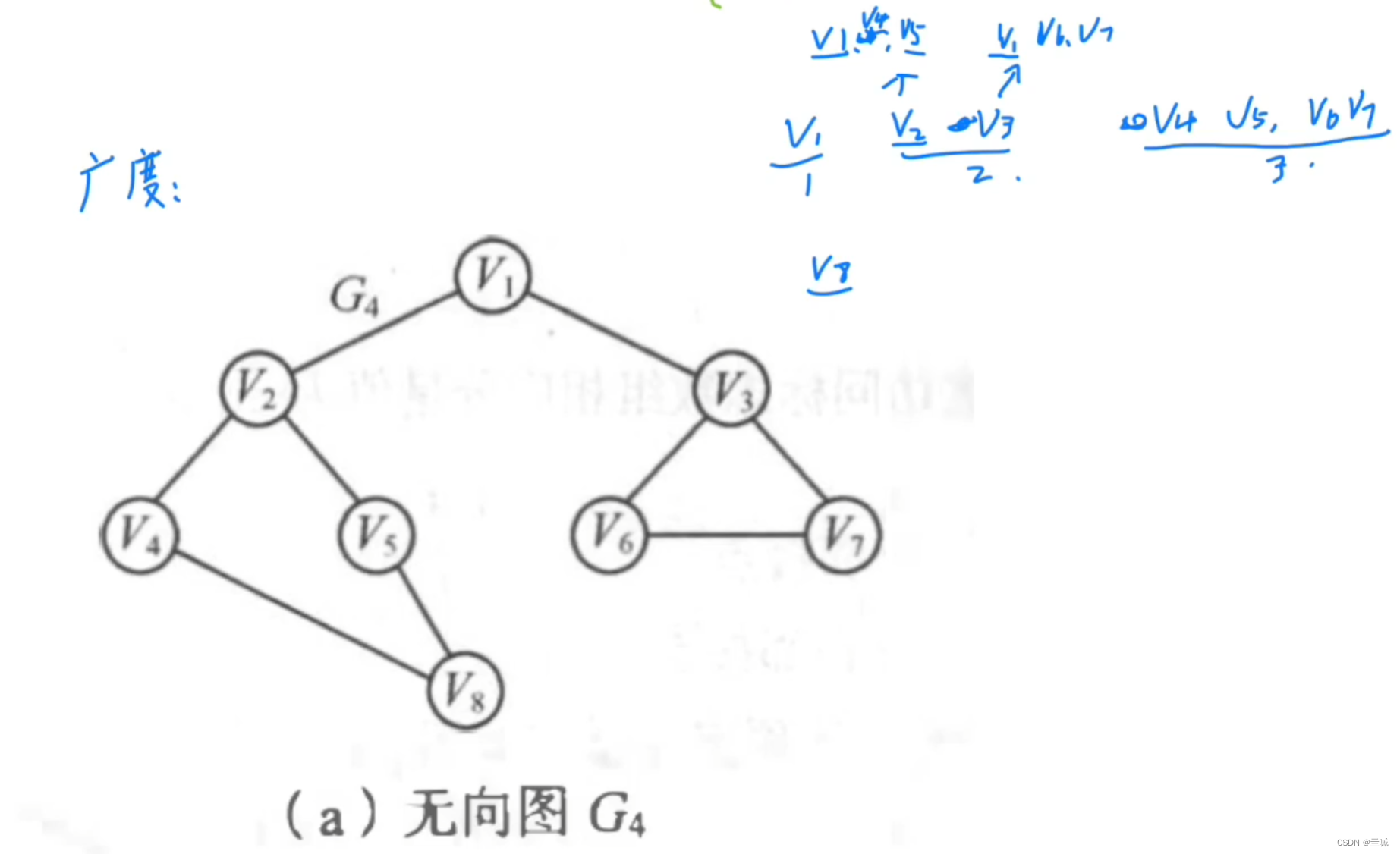
.
二分查找:
公式:mid =( low + high )/ 2
例题:
一个长度为 n 的有序表,若采用二分查找一个不存在的元素,则比较次数最多是?
公式:log 以 2 为底 n 的对数向下取整 + 1
.
前缀、中缀、后缀表达式:
相互转化:
前缀、中缀、后缀之间的相互转化都用到栈这一数据结构
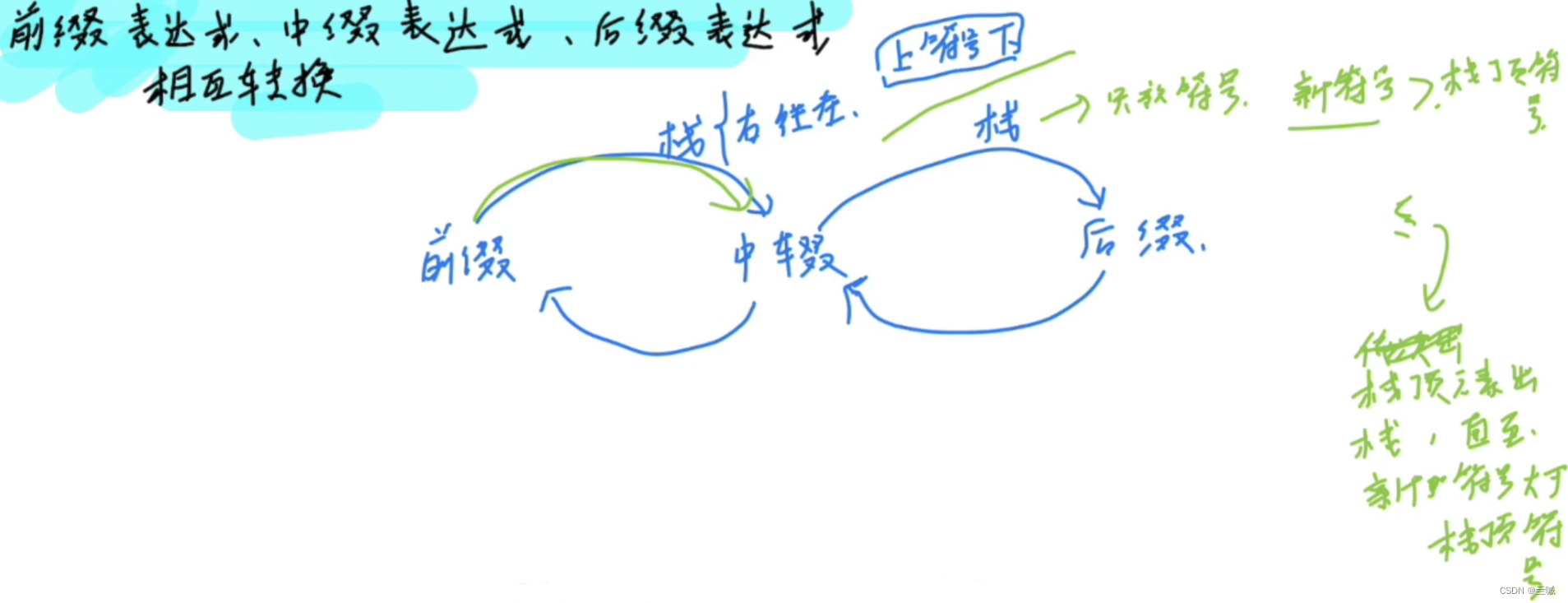
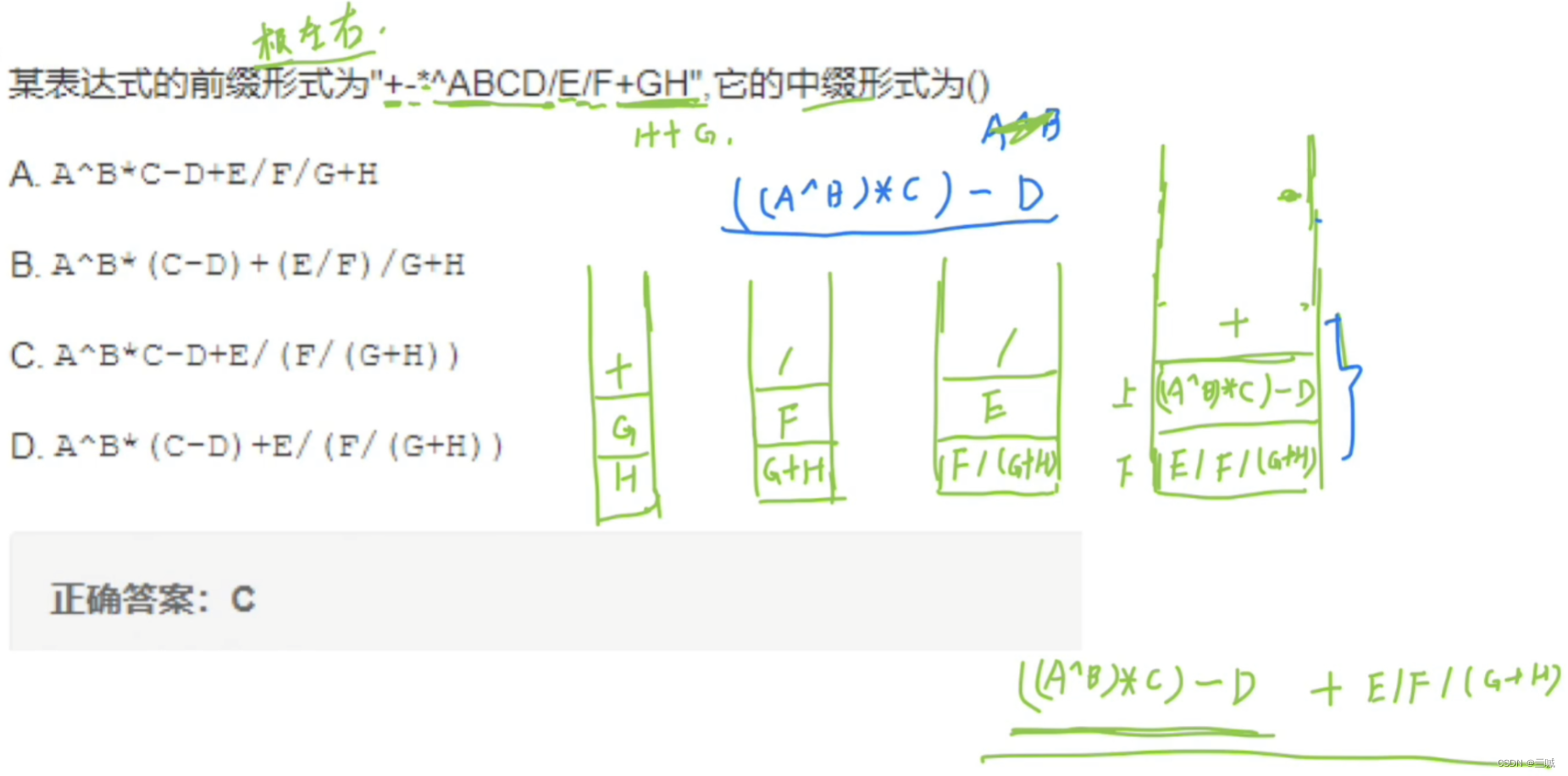
前缀转中缀:
案例:
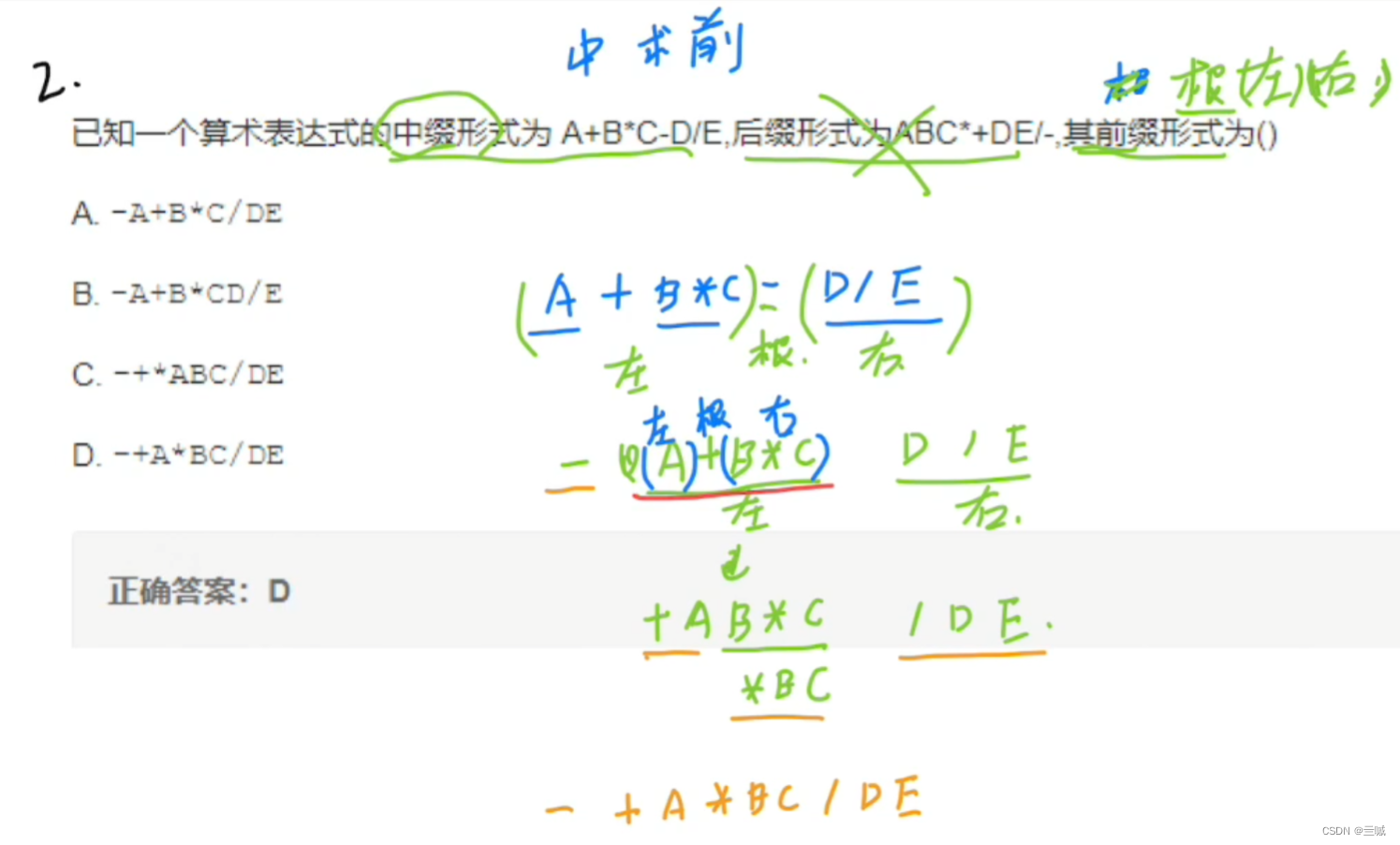
中缀求前缀:
案例:
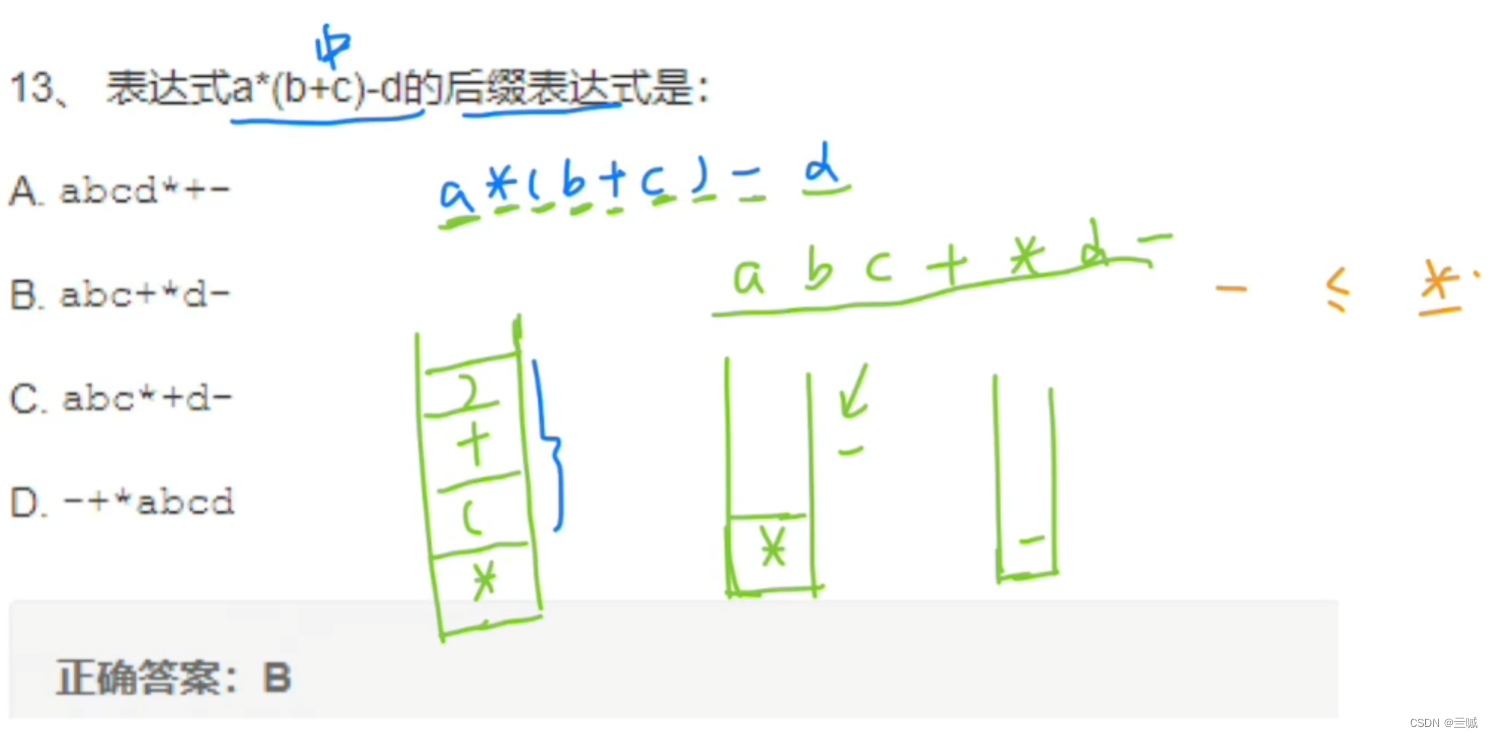
中缀求后缀:
案例:
后缀转中缀:
案例:
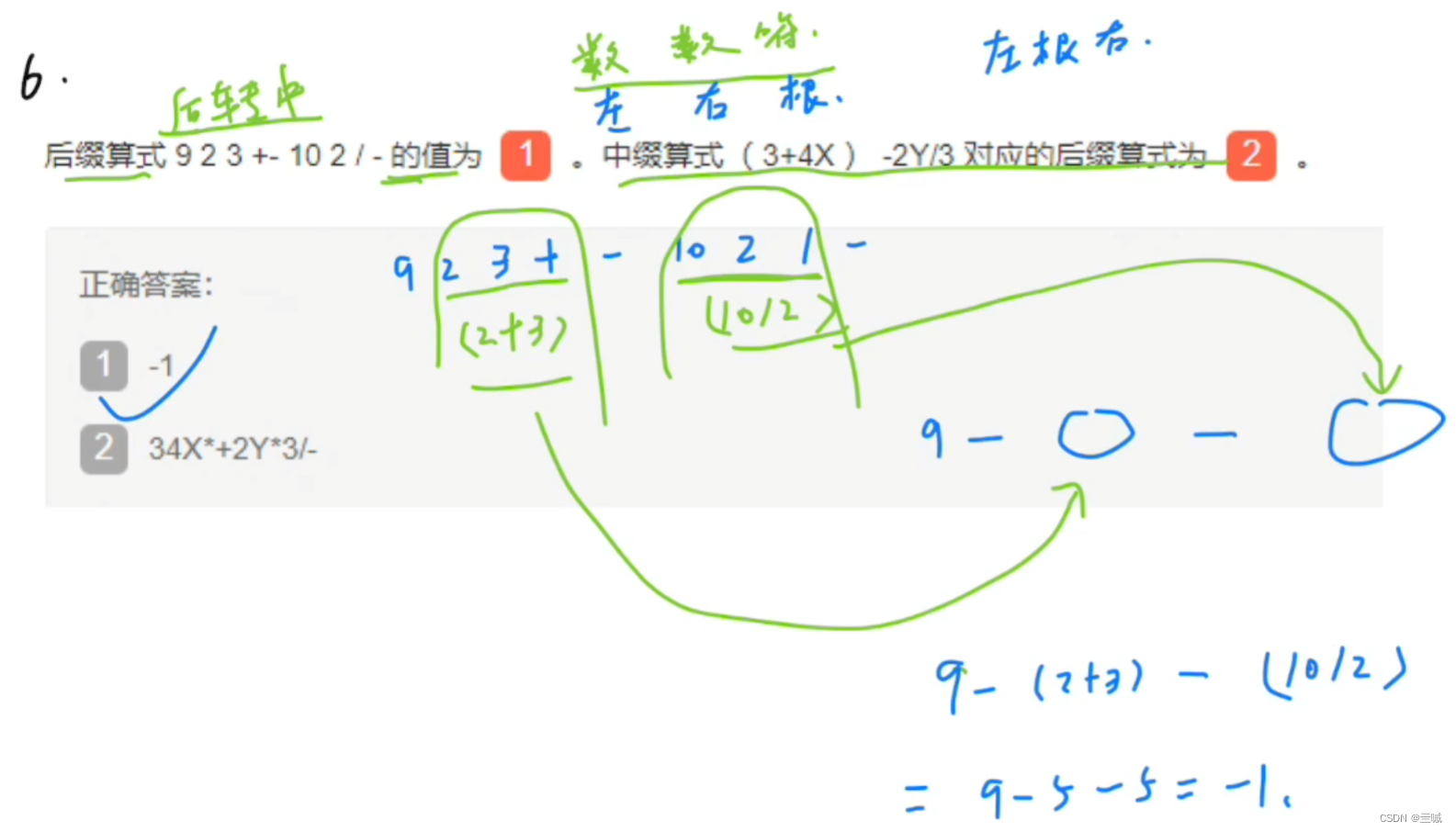
.
时间复杂度:
递归的空间复杂度为 O( n )
尾递归的空间复杂度为 O( 1 )
尾递归:
- 递归函数的最后一步操作是调用函数本身。
- 递归调用的结果不参与任何的后续操作,而是直接返回
.
排序算法时间、空间复杂度:
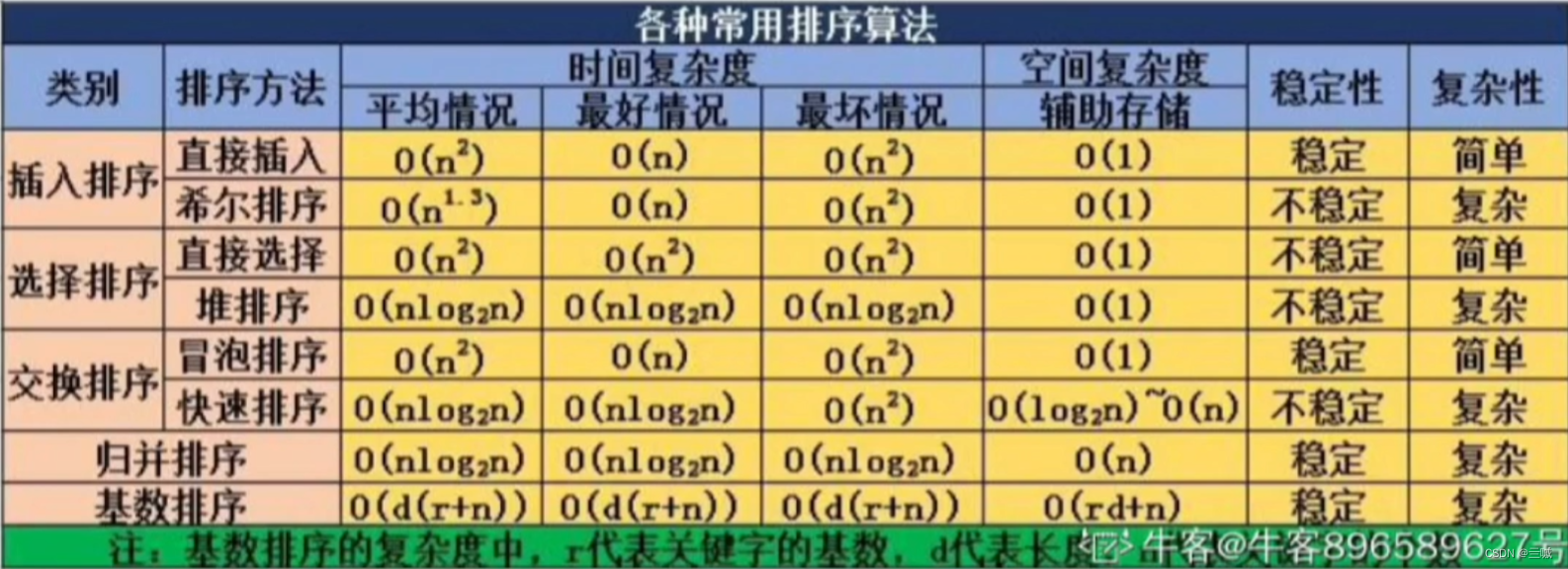
.
B - 树的插入:
B - 树类似一个结点可以容纳多个数的多叉树
B - 树中除根之外的所有非终端结点中的关键字个数必须大于等于 m / 2 的上取整 - 1,不超过 m - 1
m:阶数

.
B - 树的删除:
- 若该结点为最下层的非终端结点,由于其指针均为空,删除后不会影响其他结点,可直接删除
- 若该结点不是最下层的非终端结点,邻近的指针则指向一棵子树,不可直接删除