在前面的线性回归中，我们可以使用不同次数的多项式对数据集进行拟合，但是选择次数过低的多项式会导致欠拟合，选用次数过多的多项式会过拟合，那么如何选择合适的多项式呢？这就是本文需要解决的问题。

想要了解自己训练出的模型对训练集外的实例的泛化能力，则我们可以将初试的数据集分为两部分：70%为我们的训练集，剩下30%为我们的测试集（当然比例我们可以灵活调整）。我们通常用$m_{test}$表示测试集的数量，$(x_{test}^{(1)},y_{test}^{(1)})$表示一个测试集实例

首先我们使用梯度下降求得最小的代价函数$J(\Theta )$，然后使用测试集求其对训练集之外的实例的误差，也就是求$$J_{test}(\Theta )=\frac{1}{2m_{test}}\sum _{i=1}^{m_{test}}(h_{\theta }(x_{test}^{(i)})-y_{test}^{(i)}{)}^2$$如果是分类问题则直接将公式换成逻辑回归的代价函数计算公式便可

在过拟合中，尽管训练出来的模型对训练集拟合得十分完美，但是模型对新样本的泛化能力很差。那么我们应该如何找到最适合的假设函数的多项式次数呢？

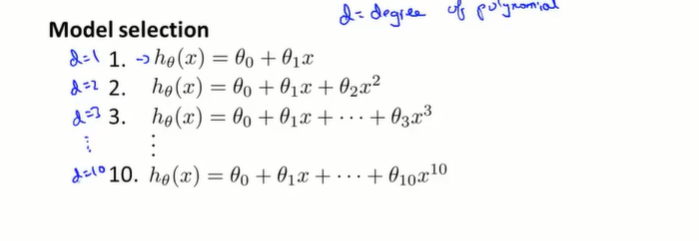
假设我们选择的多项式的次数为d，如上图。如果我们想要得到某个次数的多项式假设函数对新样本的泛化能力，我们可以这样做：首先选择d=1的假设函数来训练模型，然后用线性回归和梯度下降求出代价函数最小的时候的$\theta$的取值，我们用${\theta }^{(1)}$表示d=1的时候的$\theta$取值。同理，我们一直重复上述方法可以得到${\theta }^{(2)},{\theta }^{(3)}...{\theta }^{(10)}$，通过得到的参数，可以计算出$J_{test}({\Theta }^{(1)}),J_{test}({\Theta }^{(2)}),J_{test}({\Theta }^{(3)})...J_{test}({\Theta }^{(10)})$然后选出其中$J_{test}({\Theta }^{(i)})$最小的一个模型，假设$J_{test}({\Theta }^{(5)})$最小，那么我们会认为泛化能力最出色的多项式。但是这仍不能证明模型的泛化能力，因为上述过程类似于新增了一个参数d之后，再使用测试集进行模型训练选出最优d值，也就是说，这是使用测试集来选择模型，又使用相同的测试集来计算误差，对于模型多项式次数d的选择会存在过拟合的情况

为了解决模型选择中的过拟合的问题，我们将数据集划分为三部分：训练集、交叉验证集、测试集。一般它们之间的比例为6：2：2，比例可以灵活调整。一般我们将交叉验证集的第i个样本记作$(x_{cv}^{(i)},y_{cv}^{(i)})$。以d=2为例子，当我们面对模型选择的时候，对于从d=1到d=10的模型，我们依次使用线性回归和梯度下降求出代价函数最小的时候的$\theta$的取值，然后求出各个d的取值下$J_{cv}(\theta )$的取值，而不是像之前的求$J_{test}(\Theta )$的取值，如下图所示

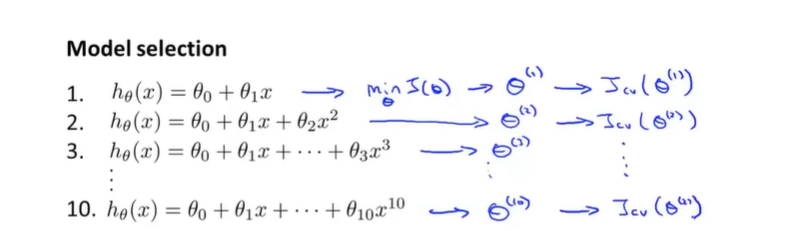
选择$J_{cv}(\theta )$值最小的对应的d的取值，假设d=4的时候最佳，那么我们就选择这个多项式次数作为最优假设函数模型。而测试集合在最后直接用于计算$J_{test}({\theta }^{(4)})$的值，这个值可以用于衡量模型对其他样本的泛化能力。生动点来说，测试集在最后选出最佳的d之后再进行测试，就如同“期末考试”一样，作为一个新样本来测试通过交叉验证集选出的d次多项式假设函数是否能够具备有良好的泛化能力