7-2

题目

理论基础

1. 矩阵的特征值和特征向量的定义以及其求法 https://www.cnblogs.com/Peyton-Li/p/9772281.html
   特征值和特征向量的定义：设$A$是$n$阶方阵，如果数$\lambda$和$n$维非零列向量$\alpha$使关系式$A\alpha =\lambda \alpha$成立，则称这样的数$\lambda$为方阵$A$的特征值，非零向量$\alpha$为$A$对应于特征值$\lambda$的特征向量。
   说明：
   特征向量$\alpha \ne O$，特征值问题是对方阵而言的。
   $n$阶方阵$A$的特征值，就是使齐次线性方程组$(\lambda I-A)x=0$有非零解的值，即满足方程$|\lambda I-A|=0$的$\lambda$都是矩阵A的特征值。
   
   $A$为$n$阶矩阵，称$\lambda I-A$为$A$的特征矩阵，其行列式$|\lambda I-A|$为$\lambda$的$n$次多项式，称为$A$的特征多项式，$(\lambda I-A)x=0$称为A的特征方程。
   

2. 求矩阵的行列式
   https://www.shuxuele.com/algebra/matrix-determinant.html

3. 主成分的贡献率
   

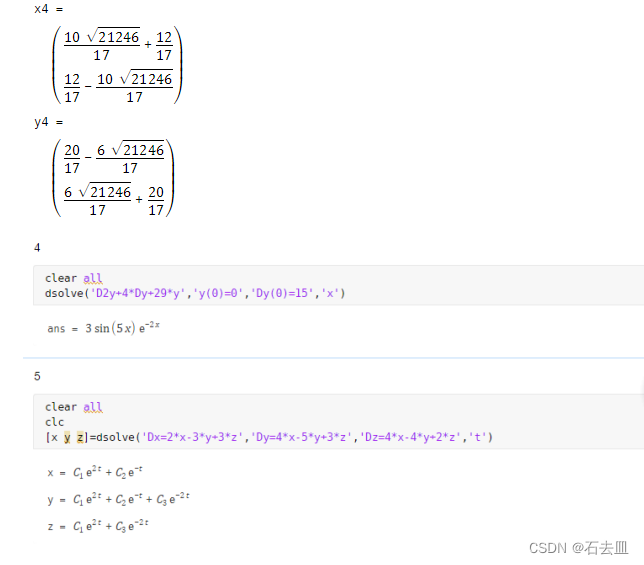
具体解题

---