PCA人脸数据降维

matlab代码实现

pictures=dir('C:\Users\Yezi\Desktop\机器学习\实验1：PCA算法\face10080\*.bmp');
sample=[];% 样本矩阵
for i=1:length(pictures)
    picture=imread("C:\Users\Yezi\Desktop\机器学习\实验1：PCA算法\face10080\"+pictures(i).name);
    picture=double(picture);
    picture=picture(:);% 单张图片拉成列向量
    sample=[sample,picture];
end
% PCA 主流程
meanFace=mean(sample); % 求样本均值
meanFace=ones(size(sample,1),1)*meanFace;% 矩阵化样本均值
sample=sample-meanFace; % 样本中心化：减去样本均值
covMatrix=sample*sample';% 求样本的协方差矩阵
[egienvectors,diagonalMatrix]=eig(covMatrix);% 协方差矩阵的特征值分解
egienvalues=diag(diagonalMatrix);% 取特征值
[egienvalues,order]=sort(egienvalues,'descend');% 特征值降序排序
egienvectors=egienvectors(:,order);% 将特征向量按特征值降序排序

思路分析

这段代码是一个简单的PCA（主成分分析）算法实现，用于对图像数据进行降维处理。下面是对代码进行逐行分析：

pictures=dir('C:\Users\Yezi\Desktop\机器学习\实验1：PCA算法\face10080\*.bmp'); 这行代码使用dir函数获取指定文件夹中的所有.bmp格式的文件名，并将结果存储在pictures变量中。
sample=[];% 样本矩阵 sample变量用于存储图像样本数据，初始化为空矩阵。
for i=1:length(pictures) for循环遍历pictures中的每个文件名。
picture=imread("C:\Users\Yezi\Desktop\机器学习\实验1：PCA算法\face10080\"+pictures(i).name); 该行代码使用imread函数读取指定路径下的图像文件，并将图像数据存储在picture变量中。
picture=double(picture); 将picture转换为double类型，以便后续计算。
picture=picture(:);% 单张图片拉成列向量 将picture变量转换为列向量的形式。
sample=[sample,picture]; 将当前处理的图像样本添加到sample矩阵中。
end for循环结束。
meanFace=mean(sample); % 求样本均值 计算sample矩阵中每个特征的均值，结果存储在meanFace变量中。
meanFace=ones(size(sample,1),1)*meanFace;% 矩阵化样本均值 将样本均值重复扩展为与sample矩阵相同大小的矩阵。
sample=sample-meanFace; % 样本中心化：减去样本均值 对sample矩阵进行样本中心化处理，即将每个样本减去对应特征的均值。
covMatrix=sample*sample';% 求样本的协方差矩阵 计算样本的协方差矩阵，即将样本矩阵乘以其转置。
[egienvectors,diagonalMatrix]=eig(covMatrix);% 协方差矩阵的特征值分解 对协方差矩阵进行特征值分解，将特征向量存储在egienvectors中，特征值存储在diagonalMatrix的对角线上。
egienvalues=diag(diagonalMatrix);% 取特征值 将特征值从diagonalMatrix的对角线提取出来，并存储在egienvalues中。
[egienvalues,order]=sort(egienvalues,'descend');% 特征值降序排序 将特征值按降序进行排序，并同时记录排序后的索引，排序结果存储在egienvalues中。
egienvectors=egienvectors(:,order);% 将特征向量按特征值降序排序 将特征向量按照特征值的降序排序，排序结果存储在egienvectors中。

以上就是给出的代码的分析，该代码主要实现了对图像数据进行PCA算法处理，得到图像数据的主成分特征向量。

PCA人脸重构

matlab代码实现

oneFace=sample(:,1);
for dimension=20:20:160
    egienvector=egienvectors(:,1:dimension);
    rebuildFace=egienvector*(egienvector'*oneFace);
    rebuildFace=reshape(rebuildFace,100,80);
    index=dimension/20;
    subplot(2,4,index);
    imshow(mat2gray(rebuildFace));
    xlabel(sprintf("dimension=%d",dimension));
end

思路分析

这段代码是用于对人脸进行重构并显示的部分，下面是对代码进行逐行分析：

oneFace=sample(:,1); 从样本中选取第一张人脸作为重构对象，将其存储在oneFace变量中。
for dimension=20:20:160 for循环迭代每个不同的维度值，从20开始，每次增加20，直到达到160。
egienvector=egienvectors(:,1:dimension); 根据给定的维度值，选择相应数量的特征向量，将它们存储在egienvector变量中。
rebuildFace=egienvector*(egienvector'*oneFace); 利用选定的特征向量重构人脸，将结果存储在rebuildFace变量中。这里的计算过程是通过将特征向量与其转置相乘来实现。
rebuildFace=reshape(rebuildFace,100,80); 将重构后的人脸变形为原始图像的大小，即100x80像素。
index=dimension/20; 计算当前维度值对应的索引，用于确定子图的位置。
subplot(2,4,index); 创建一个2x4的子图网格，并选择第index个子图作为当前维度值的显示位置。
imshow(mat2gray(rebuildFace)); 将重构的人脸图像显示在当前子图中。mat2gray函数用于将图像数据转换为灰度范围0-1之间的值，以便正确显示。
xlabel(sprintf("dimension=%d",dimension)); 在当前子图的x轴标签位置显示当前维度值。

通过以上代码，可以实现基于不同维度的特征向量重构人脸，并将结果显示在一个子图网格中。每个子图对应一个特定的维度值，同时还在每个子图上方显示该维度的标签。这样可以观察不同维度下重构人脸的效果，并比较不同维度对重建结果的影响。

PCA人脸可视化

二维

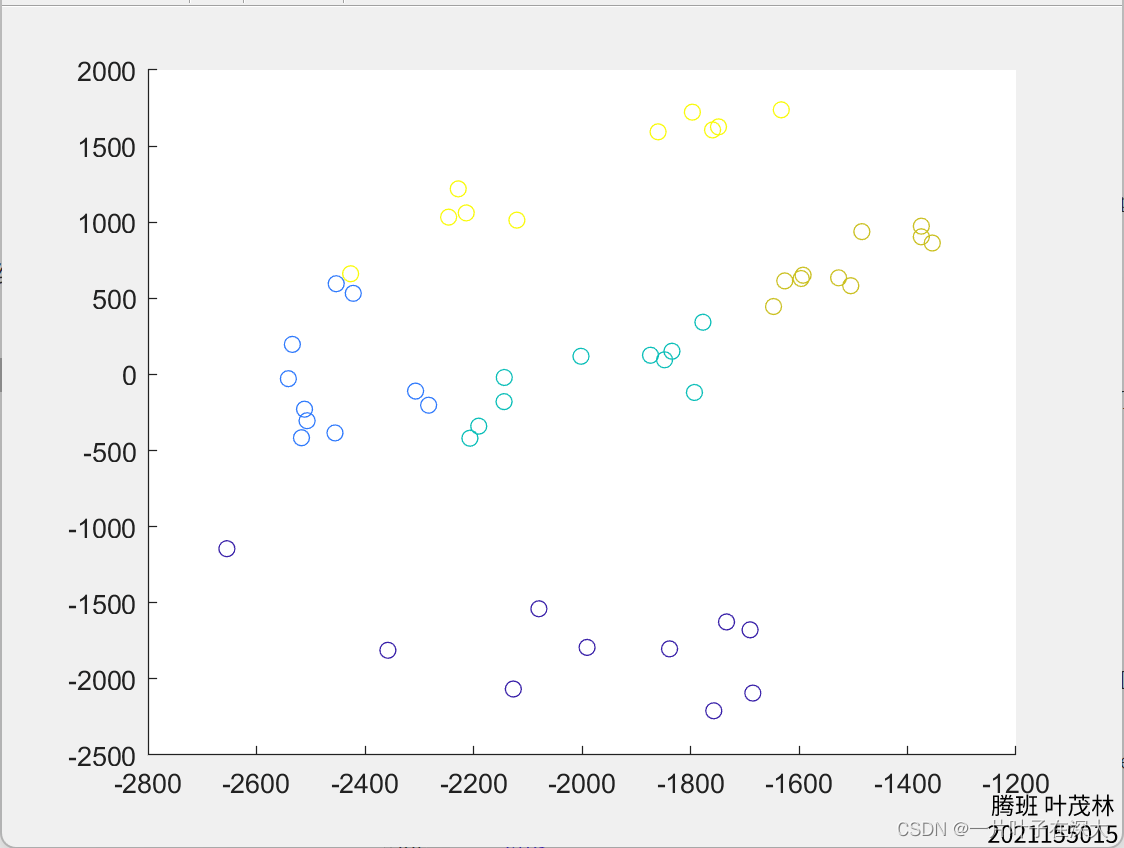
三维

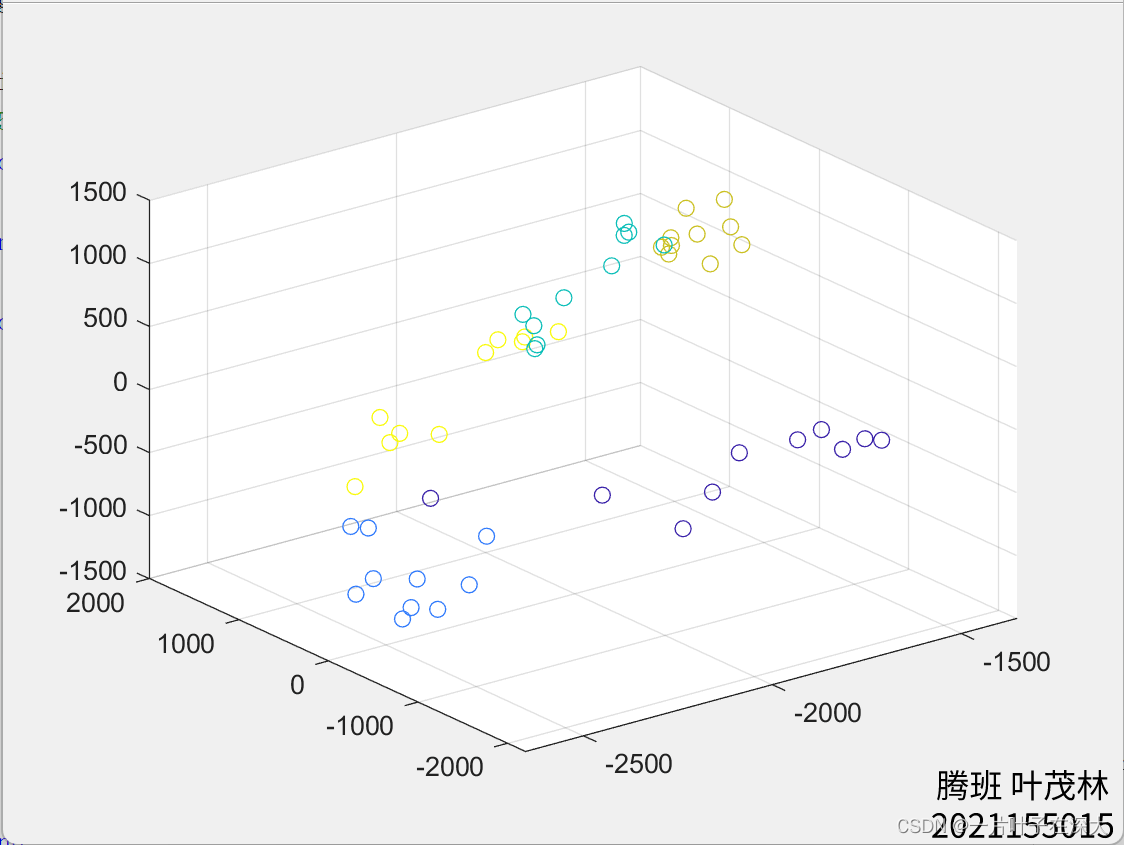
matlab代码实现

visualizeDataTemp=[];
%5个人
for i=0:4
    visualizeDataTemp=[visualizeDataTemp,sample(:,i*10+1:i*10+10)];
end

for dimension=2:3
    egienvector=egienvectors(:,1:dimension);
    visualizeData=egienvector'*visualizeDataTemp;
    colors=[];
    for i=1:50
        color=floor((i-1)/10+1)*20;
        colors=[colors,color];
    end
    if dimension==2
        scatter(visualizeData(1,:),visualizeData(2,:),[],colors);
    else
        scatter3(visualizeData(1,:),visualizeData(2,:),visualizeData(3,:),[],colors);
    end
end

思路分析：

这段代码是用于对经过PCA降维的人脸样本进行可视化的部分，下面是对代码进行逐行分析：

visualizeDataTemp=[]; 创建一个空矩阵visualizeDataTemp，用于存储可视化数据。
for i=0:4 for循环迭代5次，从0到4。
visualizeDataTemp=[visualizeDataTemp,sample(:,i*10+1:i*10+10)]; 将每个人的10个人脸样本按列连接起来，并添加到visualizeDataTemp中。这样，visualizeDataTemp将包含50个人脸样本。
for dimension=2:3 for循环遍历每个指定的维度值，从2到3。
egienvector=egienvectors(:,1:dimension); 根据给定的维度值，选择相应数量的特征向量，将它们存储在egienvector变量中。
visualizeData=egienvector'*visualizeDataTemp; 将选择的特征向量与样本数据进行相乘，得到降维后的可视化数据，存储在visualizeData变量中。
colors=[]; 创建一个空矩阵colors，用于存储数据点的颜色信息。
for i=1:50 for循环遍历50次，对于每个数据点。
color=floor((i-1)/10+1)*20; 根据数据点的索引，计算对应的颜色值。这里使用(i-1)/10+1来确定颜色分组，然后乘以20得到颜色值。
colors=[colors,color]; 将计算得到的颜色值添加到colors矩阵中。
if dimension==2 判断当前维度是否为2。
scatter(visualizeData(1,:),visualizeData(2,:),[],colors); 使用散点图将二维可视化数据绘制出来，各个数据点的坐标由visualizeData给出，颜色由colors指定。
else 如果当前维度不是2。
scatter3(visualizeData(1,:),visualizeData(2,:),visualizeData(3,:),[],colors); 使用3D散点图将三维可视化数据绘制出来，各个数据点的坐标由visualizeData给出，颜色由colors指定。

通过以上代码，可以将经过PCA降维处理的人脸样本进行可视化展示。具体而言，对于每个维度值，将选择相应数量的特征向量，并将样本数据投影到这些特征向量上，得到降维后的可视化数据。然后使用散点图或3D散点图将数据点绘制出来，并根据数据点的分组信息为其指定不同的颜色。这样可以观察不同维度下人脸样本在降维空间中的分布情况。

PCA人脸识别

不同维度的识别率

不同knnk值的识别率

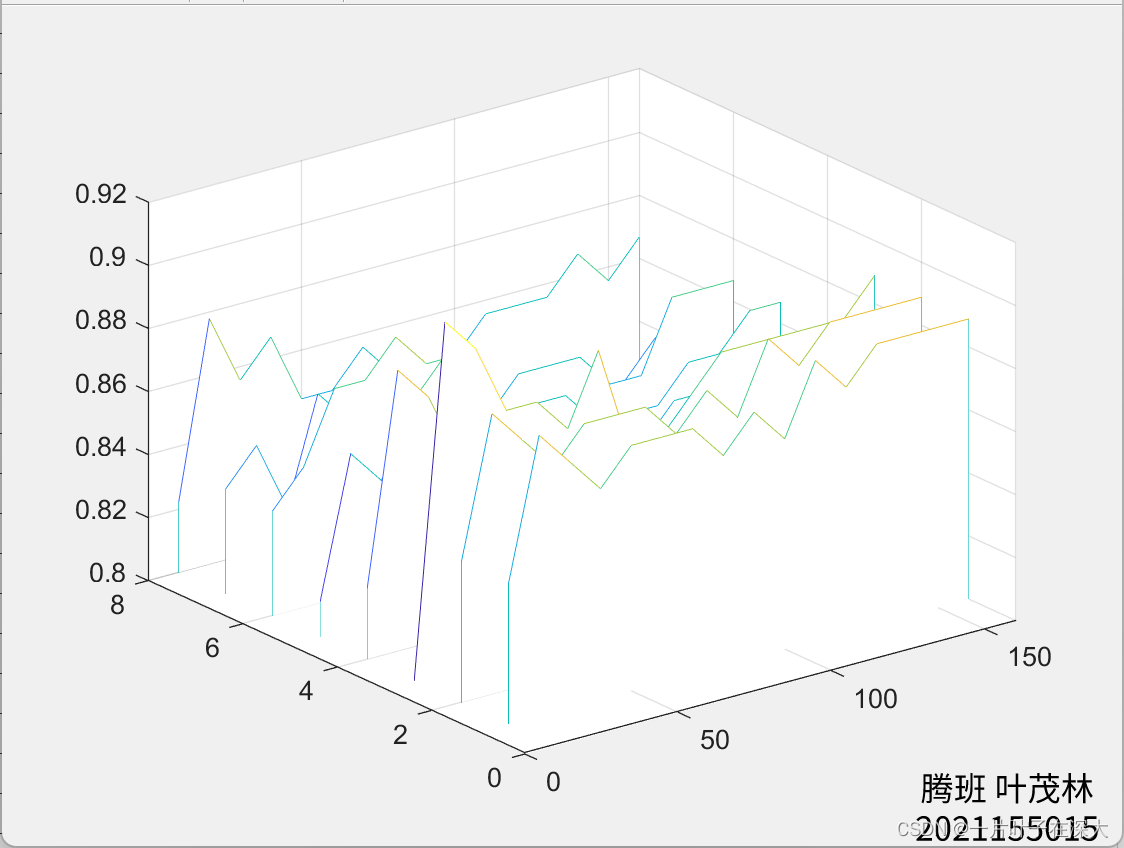
matlab代码实现

trainNumber=5;
testNumber=6;
trainData=[];
testData=[];
for i=0:14
    trainData=[trainData,sample(:,i*11+1:i*11+trainNumber)];
end
for i=0:14
    testData=[testData,sample(:,i*11+trainNumber+1:i*11+11)];
end
result=[];
for knnK=1:8
    for dimension=10:10:160
        egienvector=egienvectors(:,1:dimension);
        trainDataTemp=egienvector'*trainData;
        testDataTemp=egienvector'*testData;
        error=0;
        testDataNumber=size(testDataTemp,2);
        trainDataNumber=size(trainDataTemp,2);
        for i=1:testDataNumber
            distances=[];
            for j=1:trainDataNumber
               distance=0;
               for k=1:dimension
                  distance=distance+(testDataTemp(k,i)-trainDataTemp(k,j))^2; 
               end
               distances=[distances,distance];
            end
            [distances,index]=sort(distances);
            rightIndex=floor((i-1)/testNumber)+1;
            testIndex=0;
            knn=[];
            for k=1:knnK
               knn=[knn,floor((index(k)-1)/trainNumber)+1];
            end
            [modeIndex,times]=mode(knn);
            if times==1
                testIndex=knn(1);
            else
                testIndex=modeIndex;
            end
            if testIndex~=rightIndex
                error=error+1;
            end
        end
        rate=(testDataNumber-error)/testDataNumber;
        result=[result,rate];
    end
end
X=10:10:160;
Y=1:8;
result=reshape(result,16,8);
result=result';
waterfall(X,Y,result);%不同k值不同维度的识别率
%plot(X,mean(result));%不同维度的平均识别率