数字逻辑与模拟电子技术-部分知识点（2）——模电部分-半导体三极管、基本线性运放电路、正弦波振荡电路

news2024/11/23 9:20:25

半导体三极管

三极管的放大的条件

基本放大电路计算

基本线性运放电路

同相放大电路

反相放大电路

加法器放大电路

正弦波振荡电路

正弦波振荡的条件

半导体三极管

三极管的放大的条件

主要是依靠它的发射极电流能够通过基区传输，然后到达集电极而实现的。

实现这一传输过程的两个条件是：

（1）内部条件：发射区杂质浓度远大于基区杂质浓度，且基区很薄。

（2）外部条件：发射结正向偏置，集电结反向偏置。

基本放大电路计算

试用估算法和图解法求下图（a）所示放大电路的静态工作点，已知该电路中的三极管β=37.5，其输出特性曲线如下图（b）所示。

（1）用估算法求静态工作点

首先画出图（a）电路的直流通路如图（c）所示，由直流通路，可知：

$I_{BQ}\approx \frac{V_{CC}}{R_b}=\frac{12}{300}=0.04mA=40\mu A$

$I_{CQ}=\beta I_B=37.5\times0.04=1.5mA$

$U_{CEQ}=V_{CC}-I_{CQ}R_C=12-1.5\times4=6V$ （由KVL得到式子）

（2）用图解法求静态工作点

首先在输出特性曲线的坐标平面内作出直流负载线。由直流通路列出输出回路的直流负载线方程为： $U_{CE}=V_{CC}-I_{C}R_{C}=12-4\times I_C$

令 $I_C$ =0，得M点（12，0）；又令 $U_{CE}$ =0，得N点（0，3）。连接MN两点，即可得到直流负载线，与 $I_B=I_{BQ}=40\mu A$ 的一条输出特性曲线相交，其交点Q就是静态工作点.

如图（b）所示，从曲线上查出：IBQ=40μA，ICQ=1.5mA，UCEQ=6V 。与估算法所得结果一样。

*在下图所示电路中，已知三极管β=100， $r_{bb'}$ =200Ω， $U_{BEQ}$ =0.7V， $R_s$ =1kΩ， $R_{b1}$ =62kΩ， $R_{b2}$ =20kΩ， $R_c$ =3kΩ， $R_e$ =1.5kΩ， $R_L$ =5.6kΩ， $V_{CC}$ =15V，各电容的容量足够大。

试求：静态工作点；

$U_{BQ}=\frac{R_{b2}}{R_{b1}+R_{b2}}V_{CC}=\frac{20k\Omega }{(62+20)k\Omega }\times 15V\approx 3.7V$

$I_{CQ}\approx I_{EQ}=\frac{U_{BQ}-U_{BEQ}}{R_e}=\frac{(3.7-0.7)V}{1.5k\Omega }\approx 2mA$

$I_{BQ}=\frac{I_{CQ}}{\beta }=\frac{2mA}{100}\approx 20\mu A$

$U_{CEQ}=V_{CC}-I_{CQ}(R_c+R_e)=15V-2mA(3k\Omega +1.5k\Omega )=6V$

基本线性运放电路

同相放大电路

同向放大器的输入输出关系式： $u_o=(1+\frac{R_1}{R_2})u_i$ （后除前）

反相放大电路

反向放大器的输入输出关系式： $u_o=(-\frac{R_2}{R_1})u_i$

加法器放大电路

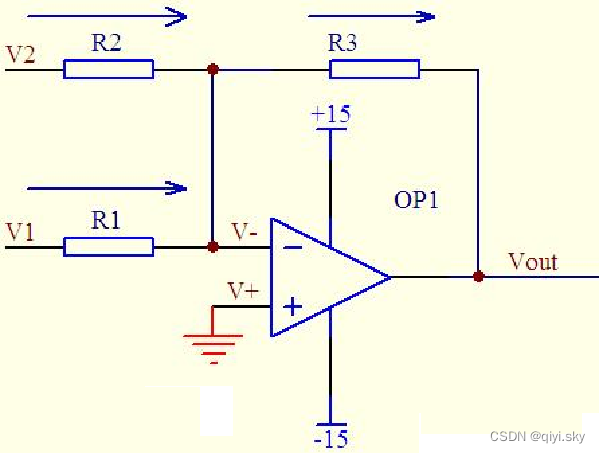
加法放大器的输入输出关系式： $U_0=\frac{R_3}{R_1}U_1+\frac{R_3}{R_2}U_2$

正弦波振荡电路

正弦波振荡的条件

一旦产生稳定的振荡，则电路的输出量自维持，即 $\overset{.}{X_o}=\overset{.}{A}\overset{.}{F}\overset{.}{X_o}$

$\overset{.}{A}\overset{.}{F}=1\Rightarrow \left\{\begin{matrix} \left | \overset{.}{A}\overset{.}{F} \right |=1\\ \varphi_A+\varphi _F=2n\pi \end{matrix}\right.$