来源:投稿 作者:橡皮
编辑:学姐

论文链接:https://arxiv.org/abs/2303.02595
论文代码:暂未发布
0. 背景
由于复杂的工业制造过程中的不可控因素,不可避免地会给产品带来不可预见的缺陷。由于人类视觉系统具有感知异常的固有能力[25],质量控制长期依赖人工检查。
然而,大规模图像和微小缺陷对人工检测来说是一项挑战,因此越来越多的研究集中在自动化机器视觉检测上。在所有方法中,有监督的深度学习取得了巨大的成功。它依靠带注释的数据集来学习判别特征,有效地克服了手工制作的缺点。然而,由于负样本不足、对标签的高要求以及缺乏先验知识,这些基于监督学习的方法在识别实践中可能会遇到看不见的缺陷。
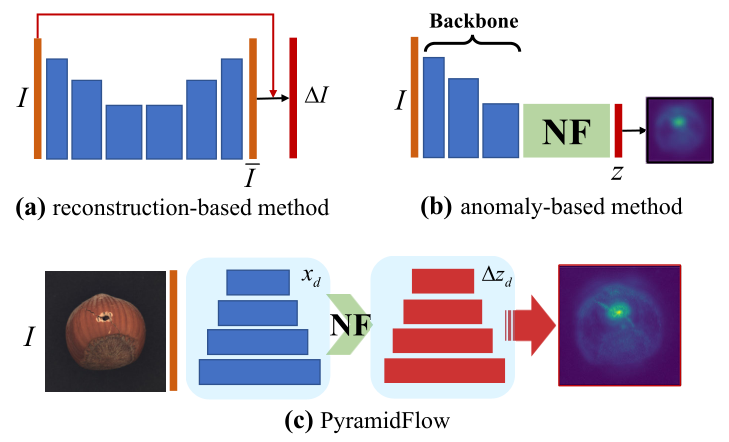
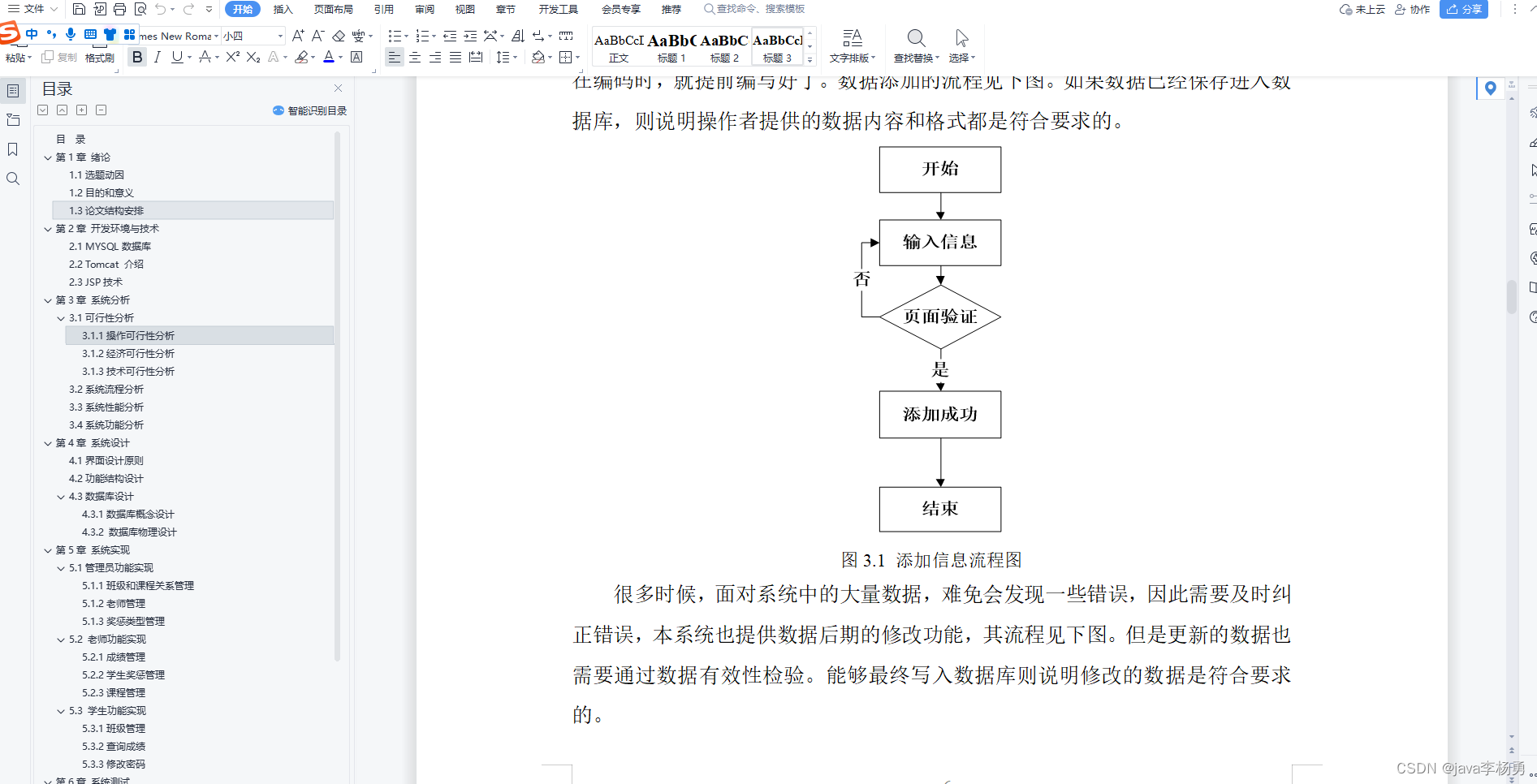
图 1. 各种异常定位方法的图示。 (a) 基于重建的方法。 (b) 基于异常的方法,其中 NF 表示归一化流。 (c) 提出的 PyramidFlow 结合了潜在模板和归一化流,可实现高分辨率定位。
最近,无监督方法已应用于缺陷检测,如图 1(a,b)所示。基于重建的方法是最著名的,它将重建图像作为模板,然后在图像空间中应用显式对比度以实现高分辨率定位。然而,使用解码器重建是一个不适定的逆问题,很难重建复杂的细节。为了克服上述限制,基于异常的方法 利用纹理感知预训练模型实现了高图像级性能,这也损害了像素级视觉性能。最有前途的方法之一是卷积归一化流,它进一步从预训练特征对概率分布进行建模,从而获得更高的性能。
1.本文主要贡献
-
提出了一种基于潜在模板的缺陷对比定位范例。与基于重建的方法类似,在潜在空间中执行对比定位,这避免了病态并有效地减少了类内方差。
-
提出 PyramidFlow,它包括用于多尺度融合和映射的可逆金字塔和金字塔耦合块,可实现高分辨率缺陷定位。此外,还提出了体积归一化以提高泛化能力。
-
进行了全面的实验,以证明提出的先进方法优于不使用外部先验的同类算法,甚至在复杂场景中实现了最先进的性能。
2.网络介绍
算法由训练和评估两个过程组成,如图 2 所示。训练过程类似于孪生网络,通过最小化图像对内的频率差异来优化模型。对于评估过程,通过在总训练数据集上进行推理获得潜在模板,然后应用潜在对比和金字塔合成来获得异常定位图。详细信息展示在以下部分中。

图 2. PyramidFlow 的训练和评估示意图。 (a) 给定任何正常图片对,尝试最小化其间潜在变量的距离。 (b) 潜在变量的均值与示例进行对比,然后应用金字塔组合来获得异常定位图。
3.1 方法细节:可逆金字塔范式
缺陷图像包含各种频率成分。通常,低频分量代表慢梯度背景,而高频分量对应于细节或缺陷。为了解耦频率分量并独立识别每个频率分量,我们提出了可逆金字塔,它可以对单个特征进行多尺度分解和组合。为了促进特征学习,以前的工作应用预训练的编码器来提取特征。尽管具有外部先验的预训练方法有助于提高性能,但为了在我们的初步研究中充分探索我们的方法的优势,让我们考虑一个没有任何预训练模型的基线。
3.2 方法细节:金字塔耦合模块
可逆模块。 可逆模块是实现可逆神经网络的基本要素。本文介绍的可逆模块有可逆卷积、可逆金字塔和仿射耦合块。仿射耦合块是构成归一化流的基本模块。它基于可逆非线性映射的特征拆分,具有易于追踪的雅可比行列式和逆运算。
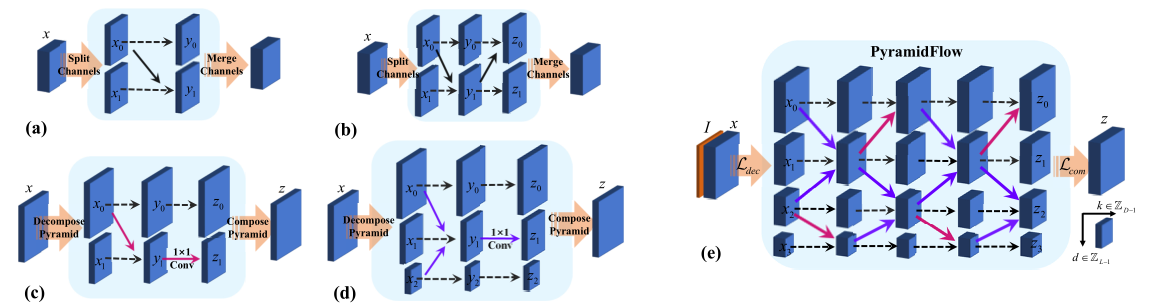
图 3. 提出的的金字塔耦合模块和 PyramidFlow,其中实线表示转换,而虚线表示同一性。 (a) 通道分裂仿射耦合块。 (b) (a)-架构的反向级联。(c) 提出的按比例金字塔耦合块。 (d) (c) 架构的逆向并行和重新参数化。 (e) 所提出的 PyramidFlow,是对 (c,d) 架构深度和层上的堆叠,其中忽略了 1 × 1 卷积来表示。
如图 3(a) 所示,传统的仿射耦合块沿通道维度拆分单个特征,其中一个子特征保持其身份,而另一个由它控制执行仿射变换。表示分割后的特征为x0,x1,其输出为y0,y1,则相应的变换可以描述为:

其中s(·)、t(·)是仿射参数,可以通过零初始化的卷积神经网络进行估计。对于式(3),有一个显式逆变换:

将s(·)中位置i、j的元素记为si,j(·)。由于变换(3)的雅可比矩阵是三角矩阵,其对数行列式可估计为:

方程(3)至(5)是所有仿射耦合块的基础。然而,图 3(a)中所示的耦合块的一部分保持相同。因此,在 NICE [8] 中提出了反向级联架构,使得两个部分都进行了转换,如图 3(b)所示。以前的工作通过迭代应用图 3(b)所示的结构来构建整体可逆归一化流。
实现。我们的方法沿尺度分解单个特征,并基于等式(3)至(5)实现多尺度特征融合。在我们的实现中,使用具有两个线性层的卷积神经网络估计多尺度仿射参数 s(·)、t(·),其中应用双线性插值来匹配目标形状。
此外,我们采用可逆 1x1 卷积 [11] 进行特征内的特征融合。具体地,将可逆1×1卷积对应的满秩矩阵记为A,可以用PLU分解📌
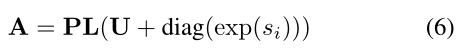
其中 P 是冻结置换矩阵,L 是具有单位对角元素的下三角矩阵,U 是具有零对角元素的上三角矩阵,exp(si) 是矩阵 A 的第 i 个特征值,它始终保持非负性.矩阵 A 在优化过程中总是可逆的,那么它的对数雅可比行列式可以估计为:
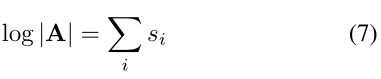
总之,方程(3)至(7)在数学上描述了所提出的金字塔耦合块,如图3(c)所示。首先,执行多尺度特征融合(3-5),然后对随机通道应用线性融合(6-7)。此外,我们提出了如图 3(d)所示的双耦合块,它等效于图 3(c)中耦合块的反向并联。双耦合块在我们的实现中被重新参数化,其仿射参数 s(·)、t(·) 是根据级联特征估计的。
体积归一化。 假设可逆变换 f : x → z 将变量 x 映射到潜在变量 z。以前的工作假设潜在变量服从基本概率分布(例如高斯分布),然后根据以下等式估计样本概率密度:

然而,这种方法依赖于基本分布假设,忽略了概率密度变换中隐式先验对泛化的影响。当将此类方法应用于异常检测时,训练目标与异常评估之间的不一致会导致域差距。
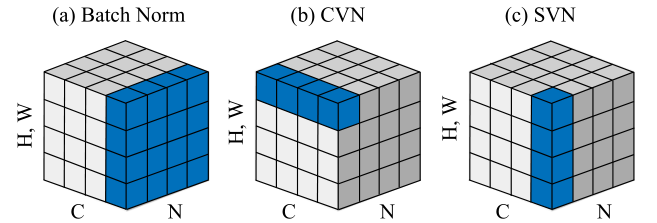
图 4. 体积归一化的图示。 (a) 批量归一化。 (b) 提出的通道体积归一化 (CVN)。 (c) 提出的的空间体积归一化 (SVN)。
类似于深度学习中的批量归一化或实例归一化,所提出的体积归一化将用于体积保持映射,如图 4 所示。特别是,对于仿射耦合块,参数 s(·) 从其均值中减去执行公式(3) 之前的值;对于可逆卷积,在根据公式(6)计算矩阵 A 之前,将参数 si 从其平均值中减去。根据统计维度,我们提出了空间体积归一化(SVN)和通道体积归一化(CVN)。 SVN 沿空间维度进行均值统计,而 CVN 沿通道维度进行。
3.3 方法细节:金字塔归一化流
结构。 我们的 PyramidFlow 可以通过将图 3(c,d) 的金字塔耦合块沿深度 D-1 次和层 L-1 次堆叠获得,如图 3(e) 所示。具体来说,PyramidFlow 使用矩阵 W 将图像 I 提取为特征 x,然后根据等式(1)执行金字塔分解。方程(3)至(7)中描述的金字塔耦合块按图3(e)描述的顺序计算得到潜在的金字塔特征zd, d = 0, 1, · · · , L − 1, 即最后根据方程(2)组合成潜在变量。
损失函数。 在体积归一化的情况下,损失函数不包括概率密度系数。此外,半正交矩阵 W 的对数雅可比行列式与样本无关,因此在训练过程中可以忽略其影响。
假设一个训练批次有 2 个正态样本,它的潜在变量是 zd(i), zd(j)。先前的研究使用空间差异训练神经网络。然而,它忽略了高频缺陷的影响。为了解决上述缺点,我们提出了以下傅立叶损失函:
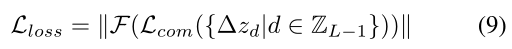
其中 F 是图像的快速傅里叶变换。使用 Eq(9) 训练归一化流使模型能够专注于高频,从而实现更快的收敛。我们将在第 4.3 节中讨论这个技巧。
缺陷定位。 以前的研究通常基于类别独立的零模板来定位具有明显差异的缺陷。在我们的方法中,缺陷被建模为相对于模板的异常偏差。然后,潜在金字塔 zd 的异常定义为,其中 ¯zd 是潜在金字塔的平均值。最后,总异常可以估计:
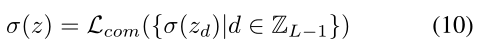
式(10)表明总异常是不同尺度异常的组合,这与Rudolph等提出的经验方法一致。
图像模板估计。 图像模板是正常样本的原型,是潜在模板的可视化。我们的完全归一化流基于 1×1 卷积而不是预训练编码器,保持端到端和近可逆性,因此可以使用方程(2)和方程(4)从潜在均值中检索流的输入 Xtemp,然后求解图像模板 Itemp 的最小二乘问题WItemp = xtemp。
4.实验结果
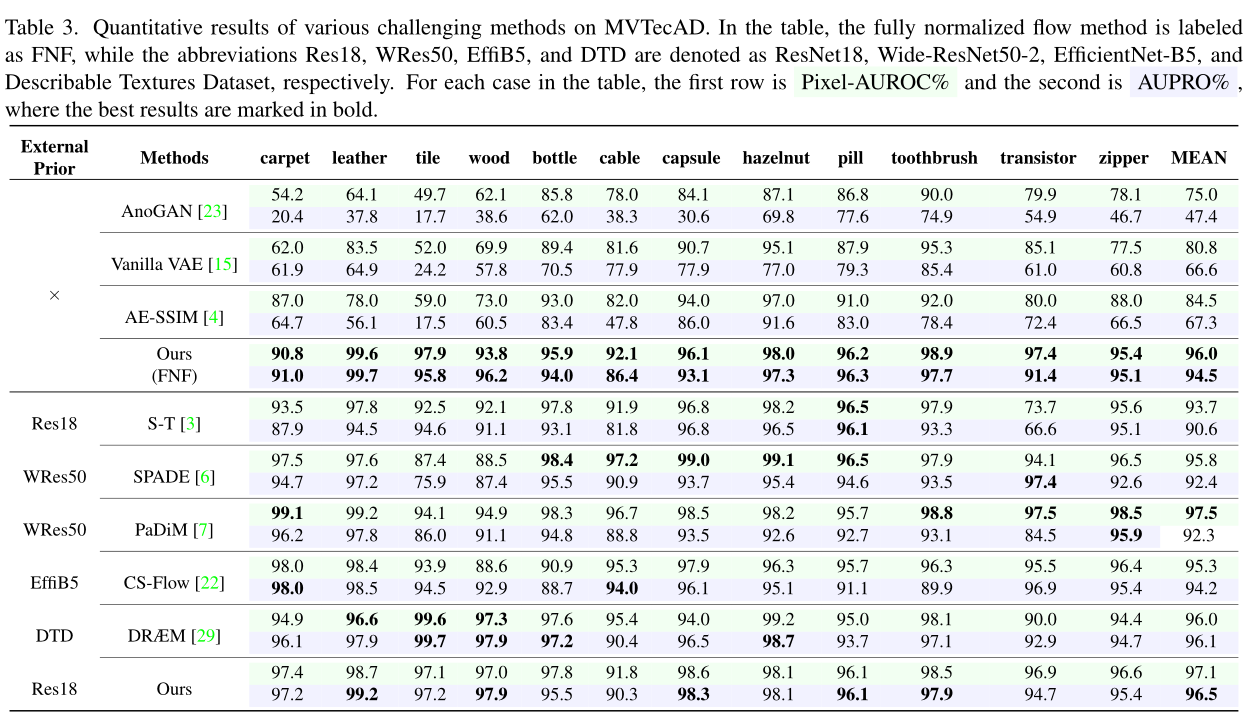
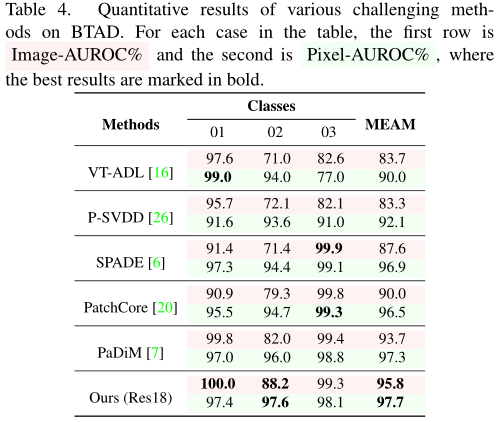
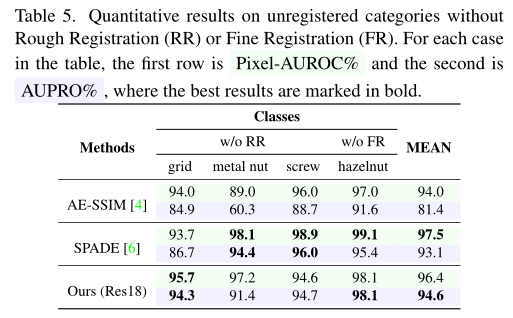
在本章中,我们对 MVTec 异常检测数据集 (MVTecAD) 和 BeanTech 异常检测数据集 (BTAD) 进行无监督异常定位实验。 MVTecAD 包含 15 类工业缺陷图像,其中五类是纹理图像,另外十类是物体图像。对象图像包含三类(网格、金属螺母、螺钉)没有粗配准和一类(榛子)没有精细配准.
4.1复杂度分析
基于等式的归一化流程。 (3) 和 (4) 在计算上是可逆的,这表明所有阶段只需要一份变量副本。此功能减少了从线性到恒定复杂度的反向传播过程中的内存占用。我们基于固定的金字塔层数 L = 8,图像分辨率为 256 × 256,通道 C = 24 分析了上述特征,然后改变堆叠层数 D 来探索内存使用和模型参数的趋势。前向和节省内存的反向传播是基于自主开发的基于 PyTorch 的 [17] 框架 autoFlow 实现的。在稳态训练期间记录所有指标,然后绘制为条形图和折线图,如图 5 所示。

4.2体积归一化研究
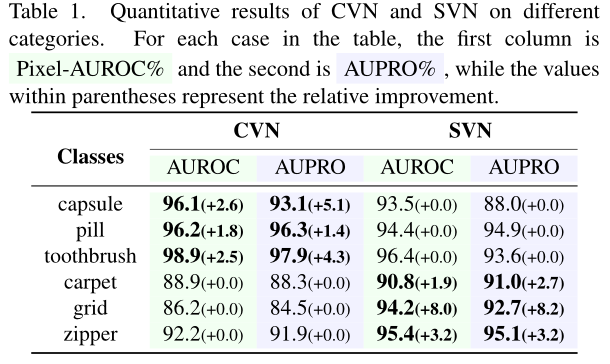

顶行显示 CVN 优级对象图像,底行显示 SVN 优级纹理图像。
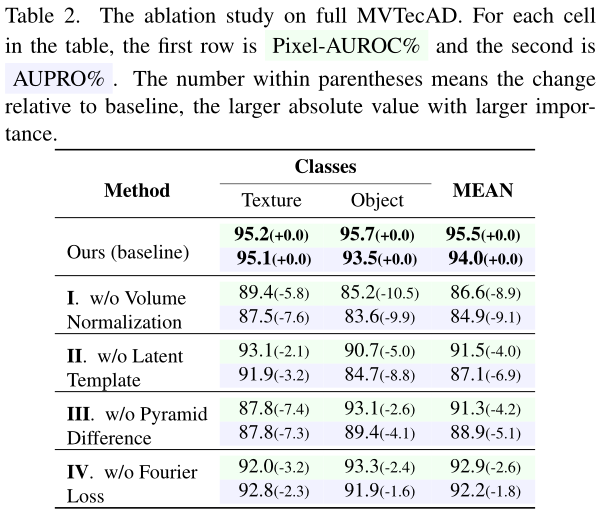
4.3消融实验

关注下方《学姐带你玩AI》🚀🚀🚀
回复“500”获取AI必读论文大合集
码字不易,欢迎大家点赞评论收藏!