FlashAttention
FlashAttention一般指的是FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness这篇,当然Transformer Quality in Linear Time这篇里非要说FLASH = Fast Linear Attention with a Single Head,命名有点无语,关于FLASH的细节参考 FLASH:可能是近来最有意思的高效Transformer设计 ,下面重点写写FlashAttention:
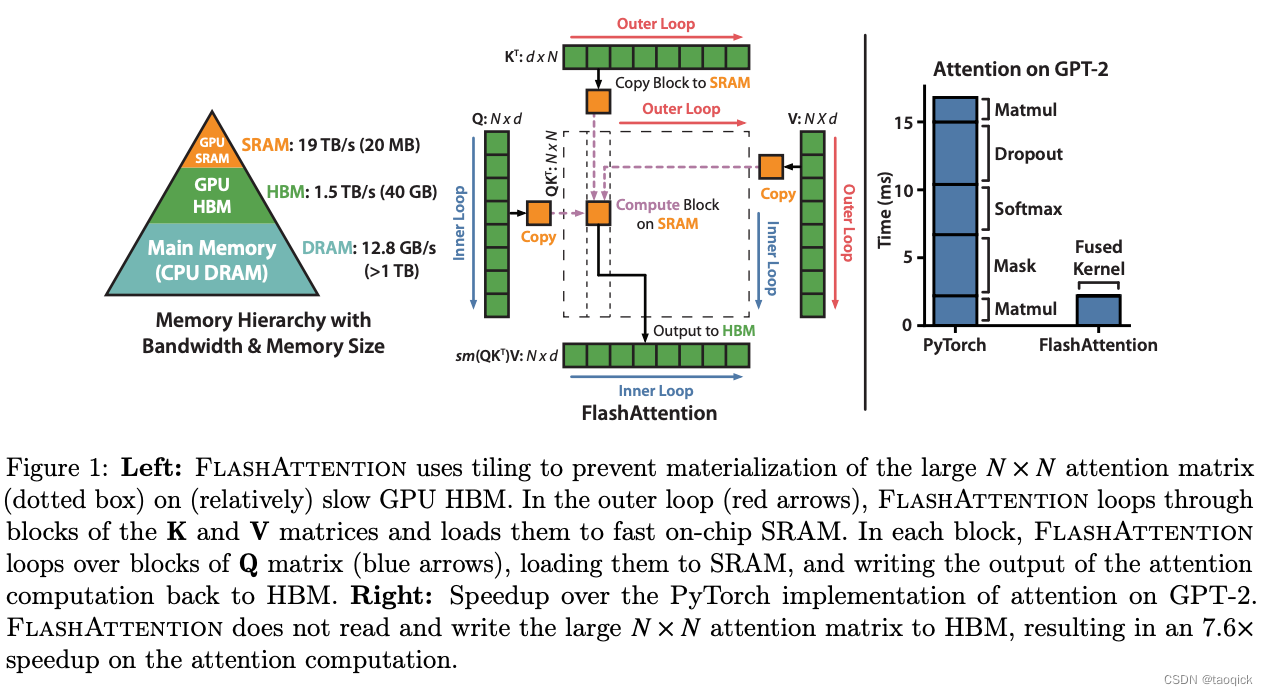
tiling中文是瓦片化,实际上就是把计算像瓦片一样铺向SRAM,保证运算不要频繁在SRAM和**HBM(High-Bandwidth Memory,HBM是高带宽内存,也就是我们常说的显存)**频繁切换,提高速度。
标准注意力的内存复杂度
对于标准注意力实现,初期我们需要把输入
Q
,
K
,
V
\mathbf{Q}, \mathbf{K}, \mathbf{V}
Q,K,V从HBM中读取,并计算完毕后把输出
O
\mathbf{O}
O写入到HBM中。
第一步把
Q
,
K
\mathbf{Q}, \mathbf{K}
Q,K读取出来计算出
S
=
Q
K
⊤
\mathbf{S}=\mathbf{Q K}^{\top}
S=QK⊤,然后把
S
\mathbf{S}
S存回去,内存访问复杂度
Θ
(
N
d
+
N
2
)
\Theta\left(N d+N^2\right)
Θ(Nd+N2)。
第二步把 S \mathbf{S} S读取出来计算出 P = softmax ( S ) \mathbf{P}=\operatorname{softmax}(\mathbf{S}) P=softmax(S),然后把 P \mathbf{P} P存回去,内存访问复杂度 Θ ( N 2 ) \Theta\left(N^2\right) Θ(N2)。
第三步把 V , P \mathbf{V}, \mathbf{P} V,P读取出来计算出 O = P V \mathbf{O}=\mathbf{P} \mathbf{V} O=PV,然后计算出结果 O \mathbf{O} O,内存访问复杂度 Θ ( N d + N 2 ) \Theta\left(N d+N^2\right) Θ(Nd+N2)。
综上所述,整体的内存访问复杂度为 Θ ( N d + N 2 ) \Theta\left(N d+N^2\right) Θ(Nd+N2)。
FlashAttention的算法
前向传播时减少对内存的访问次数
FlashAttention关键的想法就是tile(分块),把QKV都拆成块。这里一个关键点是softmax怎么算,有点绕,简单说就是把每部分分子分母的和给存下来,归一化到相同的比例。下面是个具体的例子,
l
_
p
r
e
l\_pre
l_pre是分母缩最大倍数后的和,也是最绕的点。假设QK结果是[1,2],那么softmax结果就是
[
e
1
e
1
+
e
2
,
e
2
e
1
+
e
2
]
[\frac{e^1}{e^1+e^2},\frac{e^2}{e^1+e^2}]
[e1+e2e1,e1+e2e2]
再乘以V的结果就是:
e
1
∗
v
1
e
1
+
e
2
+
e
2
∗
v
2
e
1
+
e
2
\frac{e^1*v_1}{e^1+e^2}+\frac{e^2*v_2}{e^1+e^2}
e1+e2e1∗v1+e1+e2e2∗v2
如果拆成两步算,第一步:
c
u
r
_
s
u
m
=
e
1
∗
v
1
e
1
m
_
p
r
e
=
m
a
x
(
e
1
)
=
e
1
,
是分子
e
的和
l
_
p
r
e
=
s
u
m
(
e
1
)
=
e
1
,
是分母
e
的和
cur\_sum = \frac{e^1*v_1}{e^1} \\ m\_pre = max(e^1)=e^1,是分子e的和 \\ l\_pre = sum(e^1)=e^1,是分母e的和
cur_sum=e1e1∗v1m_pre=max(e1)=e1,是分子e的和l_pre=sum(e1)=e1,是分母e的和
第二步:
m
_
c
u
r
=
m
a
x
(
e
2
,
m
_
p
r
e
)
=
e
2
l
_
p
r
e
∗
=
e
m
_
p
r
e
−
m
_
c
u
r
=
e
1
−
2
,分母缩共同倍数后相加
l
_
c
u
r
=
s
u
m
(
e
2
−
2
)
+
l
_
p
r
e
c
u
r
_
s
u
m
=
c
u
r
_
s
u
m
∗
l
_
p
r
e
l
_
c
u
r
=
e
1
∗
v
1
e
1
∗
e
−
1
e
−
1
+
e
0
c
u
r
_
s
u
m
+
=
v
2
∗
c
u
r
_
s
u
m
l
_
p
r
e
=
e
1
∗
v
1
e
1
+
e
2
+
e
2
∗
v
2
e
1
+
e
2
m\_cur = max(e^2,m\_pre)=e^2 \\ l\_pre *= e^{m\_pre - m\_cur}=e^{1-2} ,分母缩共同倍数后相加\\ l\_cur = sum(e^{2-2})+l\_pre\\ cur\_sum=cur\_sum*\frac{l\_pre}{l\_cur}=\frac{e^1*v_1}{e^1}*\frac{e^{-1}}{e^{-1}+e^0}\\ cur\_sum+=\frac{v_2*cur\_sum}{l\_pre}=\frac{e^1*v_1}{e^1+e^2}+\frac{e^2*v_2}{e^1+e^2}
m_cur=max(e2,m_pre)=e2l_pre∗=em_pre−m_cur=e1−2,分母缩共同倍数后相加l_cur=sum(e2−2)+l_precur_sum=cur_sum∗l_curl_pre=e1e1∗v1∗e−1+e0e−1cur_sum+=l_prev2∗cur_sum=e1+e2e1∗v1+e1+e2e2∗v2
这样,在前向的过程中,我们采用分块计算的方式,避免了矩阵的存储开销,整体的运算都在SRAM内进行,降低了HBM访问次数,大大提升了计算的速度,减少了对存储的消耗。详细的复杂度分析可以参考原文和https://readpaper.feishu.cn/docx/AC7JdtLrhoKpgxxSRM8cfUounsh
反向传播时使用重新计算(recompute的方式来更新梯度)
我们这里则采用重新计算的方式来计算对应的梯度。在上面前向计算的时候我们不会存储
S
,
P
\mathbf{S}, \mathbf{P}
S,P矩阵,但是我们会存储对应的指数项之和
L
L
L来进行梯度的计算。这里不展开写了,细节可以参考原文和https://readpaper.feishu.cn/docx/AC7JdtLrhoKpgxxSRM8cfUounsh
目前,Flash Attention已经集成至torch2.0,并且社区也提供了多种实现
PagedAttention
源自vLLM: Easy, Fast, and Cheap LLM Serving with PagedAttention这篇paper,关键的技术有两点:
KVCache
KV Cache是大模型推理优化的一个常用技术,该技术以空间换时间的思想,通过使用上次推理的KV缓存,可以在不影响任何计算精度的前提下,提高推理性能,降低端到端的时延。
以GPT为代表的Decoder-Only自回归语言模型在生成每一个新的 token 时,接受所有之前生成的 tokens 作为输入。然而,对于这些先前生成的 tokens,每次生成新的 token 时都需要重新计算他们的表示,这个过程造成了大量的计算浪费。KV Cache 的引入就是为了解决这个问题。
KV Cache实质上是存储了之前计算过的 key-value 对用于下一个Token的生成。在 Transformer 结构中,self-attention 中的k_proj, v_proj会将输入的每个 token 转化为一个 key 和一个 value,然后使用这些 key-value 以及当前的query对来计算下一个 token。引入 KV Cache,我们就可以将之前生成的 tokens 对应的 key-value 对存储起来,当生成新的 token 时,直接从 KV Cache 中取出这些已经计算好的 key-value 对,再把当前token的key-value做一个连结在进行计算,这样就避免了KV的重复计算,大大提高了计算效率。
整体来说,使用KV Cache包含以下两个步骤:
- 预填充阶段:在计算第一个输出token过程中,此时Cache是空的,计算时需要为每个 transformer layer 计算并保存key cache和value cache,在输出token时Cache完成填充;FLOPs同KV Cache关闭一致,存在大量gemm操作,推理速度慢,这时属于Compute-bound类型计算。
- KV Cache阶段:在计算第二个输出token至最后一个token过程中,此时Cache是有值的,每轮推理只需读取Cache,同时将当前轮计算出的新的Key、Value追加写入至Cache;FLOPs降低,gemm变为gemv操作,推理速度相对第一阶段变快,这时属于Memory-bound类型计算。
PagedAttention
通过KV Cache的技术,我们已经可以极大地提升LLM地推理速度,但是现有的Cache仍存在一些问题,
- Large:对于LLaMA-13B中的单个序列,它占用高达1.7GB的内存。
- Dynamic:它的大小取决于序列长度,而序列长度具有高度可变和不可预测的特点。
因此,高效地管理KV Cache是一个重大挑战。现有系统(HuggingFace 默认实现是pytorch的内存分配策略)由于内存碎片化和过度预留而浪费了60%至80%的内存。
为了解决这个问题,我们引入了PagedAttention,这是一种受传统操作系统虚拟内存和分页概念启发的注意力算法。与传统的注意力算法不同,PagedAttention允许将连续的键和值存储在非连续的内存空间中。具体而言,PagedAttention将每个序列的KV缓存分成多个块,每个块包含固定数量的标记的键和值。在注意力计算过程中,PagedAttention Kernel高效地识别和获取这些块,采用并行的方式加速计算。(和ByteTransformer的思想有点像)
内存布局
由于块在内存中不需要连续存储,我们可以像操作系统的虚拟内存那样以更加灵活的方式管理键和值的缓存:可以将块看作页,标记看作字节,序列看作进程。序列的连续逻辑块通过块表映射到非连续的物理块。随着生成新的标记,序列的边长,物理块按需进行分配。
在PagedAttention中,内存浪费仅发生在序列的最后一个块中。这样就使得我们的方案接近最优的内存使用率,仅有不到4%的浪费。通过内存效率的提升,我们能够显著提升BatchSize,同时进行多个序列的推理,提高GPU利用率,从而显著提高吞吐量。
PagedAttention:Cache在物理上不必连续

使用 PagedAttention 的请求的示例生成过程
内存共享
在并行采样中,从相同的提示生成多个输出序列。在这种情况下,可以在输出序列之间共享提示的计算和内存。通过其块表,PagedAttention能够自然地实现内存共享。类似于进程共享物理页,PagedAttention中的不同序列可以通过将它们的逻辑块映射到相同的物理块来共享块。为确保安全共享,PagedAttention跟踪物理块的引用计数并实现 Copy-on-Write 机制。
通过PagedAttention的内存共享机制,极大地降低了复杂采样算法(如ParallelSampling和BeamSearch)的内存开销,使其内存使用量下降了高达55%。这项优化可以直接带来最多2.2倍的吞吐量提升,从而使得LLM服务中使用这些采样方法变得更加实用。
同时进行多输出的采样

多输出采样的物理展示

部分引用自:
- FLASH:https://arxiv.org/pdf/2202.10447.pdf
- FlashAttention:https://arxiv.org/pdf/2205.14135.pdf
- https://zhuanlan.zhihu.com/p/582606847
- https://readpaper.feishu.cn/docx/AC7JdtLrhoKpgxxSRM8cfUounsh
- https://readpaper.feishu.cn/docx/EcZxdsf4uozCoixdU3NcW03snwV
- https://zhuanlan.zhihu.com/p/638468472





![[Web程序设计]实验: Servlet基础应用](https://img-blog.csdnimg.cn/e5781a6332ed4ed3b0685c910846dd8f.jpeg)
