0. 前言
最短路径算法是一种用于计算图中两个节点之间最短路径的算法。在图论中,最短路径通常指的是图中连接两个节点的路径中具有最小权重(或成本)的路径。
以下是两种常见的最短路径算法:
-
Dijkstra算法:Dijkstra算法是一种用于在带权有向图中找到从源节点到所有其他节点的最短路径的算法。它通过不断选择当前距离最短的节点,并更新与该节点相邻节点的距离,逐步构建最短路径树。Dijkstra算法适用于没有负权边的图,时间复杂度为O(V^2),其中V是图中节点的数量。
-
Bellman-Ford算法:Bellman-Ford算法是一种用于在带权有向图中找到从源节点到所有其他节点的最短路径的算法。与Dijkstra算法不同,Bellman-Ford算法可以处理具有负权边的图。它通过进行V-1次松弛操作,其中V是图中节点的数量,来逐步减小每个节点的最短路径估计值,从而找到最短路径。Bellman-Ford算法的时间复杂度为O(V*E),其中E是图中边的数量。
这些算法可以用于解决各种实际问题,如网络路由、地图导航等。根据具体的需求和图的规模,选择合适的算法来计算最短路径。
1. 概念
当谈到最短路径算法时,有几个重要的概念需要了解:
-
图(Graph):图是由节点(或顶点)和边组成的数据结构。节点表示实体或对象,边表示节点之间的连接关系。图可以是有向的(边具有方向)或无向的(边没有方向)。
-
权重(Weight):在带权图中,每条边都会有一个权重或成本值,表示通过该边所需的代价或距离。权重可以表示为正数(表示距离或代价)或负数(表示利益或收益)。
-
路径(Path):路径是图中连接两个节点的一系列边的序列。路径可以是简单路径,即不经过重复节点的路径,或者可以包含重复节点的环路。
-
最短路径(Shortest Path):最短路径是指连接图中两个节点的路径中具有最小权重(或成本)的路径。最短路径可能有多条,取决于图中边的权重和路径的定义。
-
距离(Distance):在最短路径算法中,距离是指从一个节点到另一个节点的路径的权重或成本。
最短路径算法的目标是找到连接两个节点之间的最短路径,其中路径的长度是通过边的权重来衡量的。这些算法使用不同的策略和技术来搜索和计算最短路径,以满足特定的需求和约束条件。
2. 应用
当谈到最短路径算法时,Dijkstra算法是一个经典的选择。以下是一个使用Python实现Dijkstra算法的示例:
import heapq
def dijkstra(graph, start):
# 创建一个字典,用于存储每个节点的最短路径距离
distances = {node: float('inf') for node in graph}
# 将起始节点的最短路径距离设为0
distances[start] = 0
# 使用优先队列来存储待处理的节点
priority_queue = [(0, start)]
while priority_queue:
# 从优先队列中取出当前距离最短的节点
current_distance, current_node = heapq.heappop(priority_queue)
# 如果当前节点的距离已经大于记录的距离,则忽略该节点
if current_distance > distances[current_node]:
continue
# 遍历当前节点的邻居节点
for neighbor, weight in graph[current_node].items():
distance = current_distance + weight
# 如果经过当前节点到达邻居节点的距离更短,则更新最短路径距离
if distance < distances[neighbor]:
distances[neighbor] = distance
# 将邻居节点及其距离加入优先队列
heapq.heappush(priority_queue, (distance, neighbor))
return distances
# 示例图的邻接表表示
graph = {
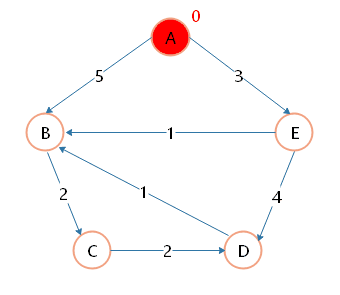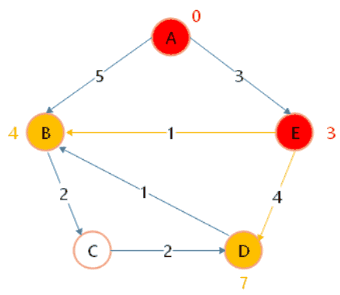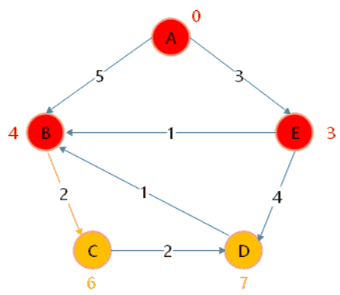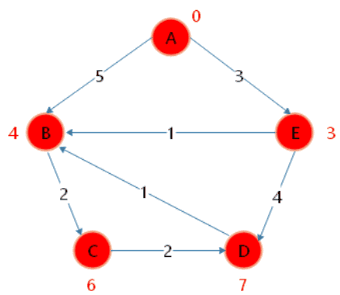
'A': {'B': 3, 'C': 2},
'B': {'A': 3, 'C': 1, 'D': 5},
'C': {'A': 2, 'B': 1, 'D': 3},
'D': {'B': 5, 'C': 3}
}
start_node = 'A'
shortest_distances = dijkstra(graph, start_node)
print(f"从节点 {start_node} 出发到达其他节点的最短路径距离:")
for node, distance in shortest_distances.items():
print(f"{node}: {distance}")
这个示例中,使用邻接表来表示图。graph变量是一个字典,其中每个键表示一个节点,对应的值是一个字典,表示该节点的邻居节点以及对应的权重。
dijkstra函数实现了Dijkstra算法。它使用了优先队列来选择当前距离最短的节点,并通过遍历邻居节点来更新最短路径距离。
最后,使用示例图中的节点’A’作为起始节点,调用dijkstra函数计算从起始节点到其他节点的最短路径距离,并打印结果。
3. 示例代码
示例:使用字典的方式构建有向图,并搜索图中的路径。
图很容易通过列表和词典来构造。比如说,这有一张简单的图:
A -> B
A -> C
A -> D
B -> E
C -> D
C -> F
D -> B
D -> E
E ->
F -> D
F -> G
G -> E
这个图有6个节点(A-G)和8个弧。它可以通过下面的Python数据结构来表示:
graph = {'A': ['B', 'C','D'],
'B': [ 'E'],
'C': ['D','F'],
'D': ['B','E','G'],
'E': [],
'F': ['D','G']
'G': ['E']}
代码
# 找到一条从start到end的路径
def findPath(graph,start,end,path=[]):
path = path + [start]
if start == end:
return path
for node in graph[start]:
if node not in path:
newpath = findPath(graph,node,end,path)
if newpath:
return newpath
return None
# 找到所有从start到end的路径
def findAllPath(graph,start,end,path=[]):
path = path +[start]
if start == end:
return [path]
paths = [] #存储所有路径
for node in graph[start]:
if node not in path:
newpaths = findAllPath(graph,node,end,path)
for newpath in newpaths:
paths.append(newpath)
return paths
# 查找最短路径
def findShortestPath(graph,start,end,path=[]):
path = path +[start]
if start == end:
return path
shortestPath = []
for node in graph[start]:
if node not in path:
newpath = findShortestPath(graph,node,end,path)
if newpath:
if not shortestPath or len(newpath)<len(shortestPath):
shortestPath = newpath
return shortestPath
'''
主程序
'''
graph = {'A': ['B', 'C','D'],
'B': [ 'E'],
'C': ['D','F'],
'D': ['B','E','G'],
'E': [],
'F': ['D','G'],
'G': ['E']}
onepath = findPath(graph,'A','G')
print('一条路径:',onepath)
allpath = findAllPath(graph,'A','G')
print('\n所有路径:',allpath)
shortpath = findShortestPath(graph,'A','G')
print('\n最短路径:',shortpath)