6466.美丽下标对数目

给你一个下标从 0 开始的整数数组 nums 。如果下标对 i、j 满足 0 ≤ i < j < nums.length ，如果 nums[i] 的 第一个数字 和 nums[j] 的 最后一个数字 互质 ，则认为 nums[i] 和 nums[j] 是一组 美丽下标对 。

返回 nums 中 美丽下标对 的总数目。

对于两个整数 x 和 y ，如果不存在大于 1 的整数可以整除它们，则认为 x 和 y 互质 。换而言之，如果 gcd(x, y) == 1 ，则认为 x 和 y 互质，其中 gcd(x, y) 是 x 和 y 最大公因数 。

示例 1：

输入：nums = [2,5,1,4]
输出：5
解释：nums 中共有 5 组美丽下标对：
i = 0 和 j = 1 ：nums[0] 的第一个数字是 2 ，nums[1] 的最后一个数字是 5 。2 和 5 互质，因此 gcd(2,5) == 1 。
i = 0 和 j = 2 ：nums[0] 的第一个数字是 2 ，nums[1] 的最后一个数字是 1 。2 和 5 互质，因此 gcd(2,1) == 1 。
i = 1 和 j = 2 ：nums[0] 的第一个数字是 5 ，nums[1] 的最后一个数字是 1 。2 和 5 互质，因此 gcd(5,1) == 1 。
i = 1 和 j = 3 ：nums[0] 的第一个数字是 5 ，nums[1] 的最后一个数字是 4 。2 和 5 互质，因此 gcd(5,4) == 1 。
i = 2 和 j = 3 ：nums[0] 的第一个数字是 1 ，nums[1] 的最后一个数字是 4 。2 和 5 互质，因此 gcd(1,4) == 1 。
因此，返回 5 。

示例 2：

输入：nums = [11,21,12]
输出：2
解释：共有 2 组美丽下标对：
i = 0 和 j = 1 ：nums[0] 的第一个数字是 1 ，nums[1] 的最后一个数字是 1 。gcd(1,1) == 1 。
i = 0 和 j = 2 ：nums[0] 的第一个数字是 1 ，nums[1] 的最后一个数字是 2 。gcd(1,2) == 1 。
因此，返回 2 。

提示：

• 2 <= nums.length <= 100
• 1 <= nums[i] <= 9999
• nums[i] % 10 != 0

思路

这个问题的基本思路是遍历数组中的所有可能的下标对 (i, j)，然后检查每一对下标的数字是否满足条件，即 nums[i] 的第一个数字和 nums[j] 的最后一个数字互质。如果满足条件，我们就将计数器增加1。最后返回计数器的值即可。

因为本题提示中2 <= nums.length <= 100，因此可以接受O(n^2)的算法，也就是说直接使用两层for循环的暴力搜索是可以的。

互质的含义

本题一个重要思路就是搞清楚互质是什么意思。"互质"是数学中的一个术语，指两个或者多个整数公约数只有1，也就是说他们没有其他共同的因子。例如，15和28互质，因为15的因子有1,3,5,15，而28的因子有1,2,4,7,14,28，除了1以外，他们没有共同的因子。

在这个问题中，我们需要检查两个数字是否互质。最直接的方法是计算他们的最大公约数（GCD）。如果GCD等于1，那么我们就可以说这两个数字是互质的。这就是为什么我们需要计算GCD的原因。

Python的标准库中有一个计算GCD的函数：math.gcd()。我们可以直接使用这个函数来计算两个数字的GCD。

然而，C++的标准库中并没有一个直接计算GCD的函数。但是，我们可以使用递归的欧几里得算法来计算GCD，这是一个非常古老且有效的算法。这个算法基于一个事实：对于任何两个整数a和b，gcd(a, b)和gcd(b, a % b)是相同的。也就是下面的写法：

// 定义一个函数计算最大公约数
    int gcd(int a, int b) {
        if (b == 0) return a;
        return gcd(b, a % b);
    }

CPP最好记住这种计算最大公约数的方法

python写法

首先，我们需要一个辅助函数来计算两个数的最大公约数（gcd）：

这道题因为python存在自带的计算gcd方式，所以python相对简单一些。

from math import gcd

def beautiful_pairs(nums):
    # 定义一个函数来获取一个数字的第一个和最后一个数字
    def get_first_last_digits(num):
        first_digit = int(str(num)[0])  # 转换为字符串并获取第一个字符，然后再转回整数
        last_digit = int(str(num)[-1])  # 转换为字符串并获取最后一个字符，然后再转回整数
        return first_digit, last_digit

    count = 0
    for i in range(len(nums)):  # 遍历每一个下标 i
        for j in range(i+1, len(nums)):  # 对每一个 i，遍历所有可能的 j
            first_digit_i, _ = get_first_last_digits(nums[i])  # 获取 nums[i] 的第一个数字
            _, last_digit_j = get_first_last_digits(nums[j])  # 获取 nums[j] 的最后一个数字
            if gcd(first_digit_i, last_digit_j) == 1:  # 如果两者互质，计数器加 1
                count += 1
    return count  # 返回总数

在这个函数中，首先创建了一个用来获取数字的第一位和最后一位的辅助函数 get_first_last_digits。然后，对于 nums 中的每一对 (i, j)，我都检查了 nums[i] 的第一个数字和 nums[j] 的最后一个数字的最大公约数是否为1。如果是，我就把计数器 count 加1。最后，函数返回总的美丽下标对数量。

注意，这个解决方案的时间复杂度为 O(n^2)，其中 n 是 nums 的长度。这是因为我们需要检查 nums 中所有的下标对。如果 nums 非常大，那么这个解决方案可能会很慢。为了提高效率，我们可能需要找到一种更快的算法或者使用一些可以加速查找的数据结构。

cpp写法

• 注意获取第一个数字和最后一个数字的方法，/10就是获取了少了最后一位的数字，一直/除到num<10，就得到了第一位数字！
• 获取最后一位数字就是**%10**

class Solution {
public:
    // 定义一个函数计算最大公约数
    int gcd(int a, int b) {
        if (b == 0) return a;
        return gcd(b, a % b);
    }

    // 定义一个函数获取数字的第一个数字
    int get_first_digit(int num) {
        while(num >= 10) {
            num /= 10;
        }
        return num;
    }

    // 定义一个函数获取数字的最后一个数字
    int get_last_digit(int num) {
        return num % 10;
    }
    int countBeautifulPairs(vector<int>& nums) {
        int count = 0;
        for (int i = 0; i < nums.size(); ++i) {  // 遍历每一个下标 i
            for (int j = i + 1; j < nums.size(); ++j) {  // 对每一个 i，遍历所有可能的 j
                int first_digit_i = get_first_digit(nums[i]);  // 获取 nums[i] 的第一个数字
                int last_digit_j = get_last_digit(nums[j]);  // 获取 nums[j] 的最后一个数字
                if (gcd(first_digit_i, last_digit_j) == 1) {  // 如果两者互质，计数器加 1
                    ++count;
                }
            }
        }
        return count;  // 返回总数
    }
};

这个程序首先定义了一个gcd函数来计算两个数字的最大公约数，然后定义了get_first_digit和get_last_digit函数来获取一个数字的第一位和最后一位。最后，beautiful_pairs函数计算符合条件的下标对的数量。同样，这个解决方案的时间复杂度为O(n^2)，如果数组非常大，这个解决方案可能会比较慢。

6910. 将数组划分成若干好子数组的方式

给你一个二元数组 nums 。

如果数组中的某个子数组 恰好 只存在 一 个值为 1 的元素，则认为该子数组是一个 好子数组 。

请你统计将数组 nums 划分成若干 好子数组 的方法数，并以整数形式返回。由于数字可能很大，返回其对 10^9 + 7 取余 之后的结果。

子数组是数组中的一个连续 非空 元素序列。

示例 1：

输入：nums = [0,1,0,0,1]
输出：3
解释：存在 3 种可以将 nums 划分成若干好子数组的方式：

- [0,1] [0,0,1]
- [0,1,0] [0,1]
- [0,1,0,0] [1]

示例 2：

输入：nums = [0,1,0]
输出：1
解释：存在 1 种可以将 nums 划分成若干好子数组的方式：
- [0,1,0]

提示：

• 1 <= nums.length <= 10^5
• 0 <= nums[i] <= 1

思路

基本思路是，统计数组中值为1的元素的位置，然后计算相邻两个位置之间的差值，用这些差值来计算总的方法数量。

这是基于这样一个事实：任意一个子数组只有一个1的条件下，其位置必然位于这个子数组的两个1的位置之间。在确定了子数组的1的位置之后，我们可以将该子数组在两个1之间的任意位置分割开来，从而得到一个新的好子数组。

这个题目需要我们返回结果对10^9 + 7取余的结果，原因是可能的方法数量可能会非常大，直接返回可能会导致溢出。取模操作可以保证我们的结果在一个固定的范围内，同时也满足题目的要求。

完整版

• 1e9 就是 10^9 的意思。这是科学计数法的表示方式，e 表示 “乘以10的…次方”

#include <vector>

using namespace std;

class Solution {
public:
    int numberOfGoodSubarraySplits(vector<int>& nums) {
        const int MOD = 1e9 + 7;  // 定义模数
        int n = nums.size();  // 计算数组大小
        vector<long long> ls;  // 创建一个ls数组用于存储所有的1的位置
        for (int i = 0; i < n; ++i) {  // 遍历原始数组
            if (nums[i] == 1) {  // 如果当前数字是1
                ls.push_back(i);  // 将其位置添加到ls数组
            }
        }
        if (ls.size() == 0) {  // 如果ls数组的大小为0，说明没有找到任何1，所以返回0
            return 0;
        }
        long long ans = 1;  // 初始化结果为1
        for (int i = 0; i < ls.size() - 1; ++i) {  // 遍历ls数组
            ans = (ans * (ls[i + 1] - ls[i])) % MOD;  // 更新结果为当前结果乘以两个相邻位置的差，然后取模
        }
        return ans;  // 返回最终结果
    }
};

ans = (ans * (ls[i + 1] - ls[i]))含义

ls[i] 是当前的1的下标，ls[i + 1] 是下一个1的下标。因为根据题目，一个好的子数组中只能有一个1。假设当前的1的下标是 ls[i]，那么下一个1的下标就是 ls[i + 1]。这就意味着在这两个1之间的所有数，都可以作为一个独立的子数组的一部分。这个子数组就是一个"好的"子数组，因为它只有一个1，而且这个1就是 ls[i] 或者 ls[i + 1]。

那么，在 ls[i] 和 ls[i + 1] 之间有多少种方法可以形成一个子数组呢？这就等于 ls[i + 1] - ls[i]，因为每一个在这两个1之间的位置都可以作为一个子数组的结束位置，每种结束位置对应一种方法。

在整个过程中，ans 存储的是所有可能的方法数，开始的时候我们初始化 ans 为1，然后每次都更新 ans 为 ans 乘以 ls[i + 1] - ls[i]，然后对 MOD 取模。这样做的目的是为了避免结果过大导致溢出，同时也满足题目的要求。

重要问题1：为什么ls[i + 1] - ls[i]能代表所有这两个1划分出来的子数组？

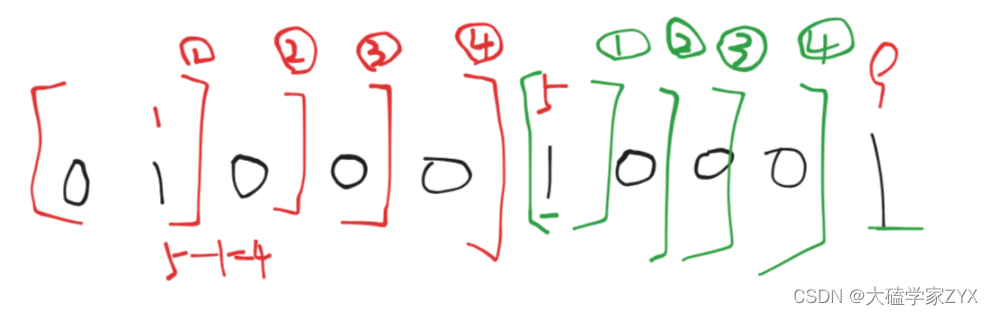
因为 ls[i + 1] - ls[i] 表示了两个连续1之间的元素数量，也就是这段区间内可以划分出来的子数组的数量。我们知道，在数组中，子数组必须是连续的元素序列。那么在两个连续的1之间（不包括这两个1），所有的子数组都是好的子数组（满足题目条件的子数组），因为这些子数组中不包含1。

例如，对于数组 [0, 1, 0, 0, 0, 1, 0, 0, 0, 1]，1的位置为 ls=[1, 5, 9]，ls[i + 1] - ls[i] 就是 [4, 4]，意味着在第一个和第二个1之间有4个元素，这4个元素可以划分出4种子数组（对应4种方法），同理，第二个和第三个1之间也有4种方法。所以总的方法数量就是 4*4=16。这16种方法包括了所有可能的划分方法，每种方法都保证了每个子数组中只有一个1。

重要问题2：为什么需要ans累乘而不是累加？

既然相减可以得到当前1对应的方法数，那么直接用(ls[i + 1] - ls[i])表示每个1对应的方法数，再进行累加不行吗？为什么要对ls数组中，每一组(ls[i + 1] - ls[i])不是与之前的结果相加，而是相乘？

可以举个例子，假设我们有一个数组[0, 1, 0, 1, 0, 1]，这里的1的位置分别是1, 3, 5，然后得到的(ls[i + 1] - ls[i])分别是2和2，也就是说在第一个1和第二个1之间有2个位置可以划分，第二个1和第三个1之间也有2个位置可以划分。

如果我们只简单地把这些数相加，就会得到2+2=4种方法，但实际上有更多的方法，我们还可以选择在第一个1和第三个1之间的任意位置划分！也就是类似下图橙色线条的情况。

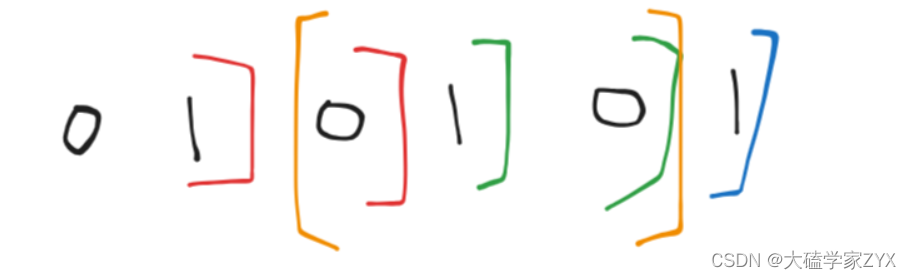
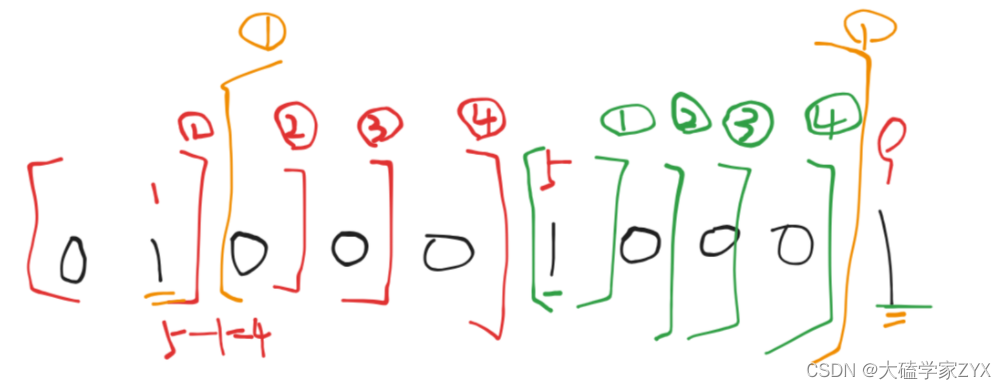
所以第一张图，总的方法数应该是2*2=4种方法。第二张图是4 * 4=16种方法。

6471. 得到整数零需要执行的最少操作数(较难，可以暂时放弃)

给你两个整数：num1 和 num2 。

在一步操作中，你需要从范围 [0, 60] 中选出一个整数 i ，并从 num1 减去 2i + num2 。

请你计算，要想使 num1 等于 0 需要执行的最少操作数，并以整数形式返回。

如果无法使 num1 等于 0 ，返回 -1 。

示例 1：

输入：num1 = 3, num2 = -2
输出：3
解释：可以执行下述步骤使 3 等于 0 ：
- 选择 i = 2 ，并从 3 减去 22 + (-2) ，num1 = 3 - (4 + (-2)) = 1 。
- 选择 i = 2 ，并从 1 减去 22 + (-2) ，num1 = 1 - (4 + (-2)) = -1 。
- 选择 i = 0 ，并从 -1 减去 20 + (-2) ，num1 = (-1) - (1 + (-2)) = 0 。
可以证明 3 是需要执行的最少操作数。

示例 2：

输入：num1 = 5, num2 = 7
输出：-1
解释：可以证明，执行操作无法使 5 等于 0 。

提示：

• 1 <= num1 <= 109

• -109 <= num2 <= 109

第一种做法：动态规划

#include <vector>
#include <algorithm>

using namespace std;

const int MAX_N = 30;
const int MAX_VAL = 1e6;
vector<vector<int>> dp;

int solve(int num1, int num2, int i) {
    if (num1 == 0) return 0;
    if (i == 0) return -1;
    if (dp[num1][i] != -1) return dp[num1][i];
    int res = -1;
    int take_i = solve(num1 - (1 << i) - num2 + MAX_VAL, num2, i - 1);
    int not_take_i = solve(num1, num2, i - 1);
    if (take_i != -1) res = min(res == -1 ? MAX_VAL : res, take_i + 1);
    if (not_take_i != -1) res = min(res == -1 ? MAX_VAL : res, not_take_i);
    return dp[num1][i] = res;
}

int minOperations(int num1, int num2) {
    dp = vector<vector<int>>(2 * MAX_VAL + 1, vector<int>(MAX_N + 1, -1));
    int res = solve(num1 + MAX_VAL, num2, MAX_N);
    return res >= MAX_VAL ? -1 : res;
}

报错：Char 34: runtime error: addition of unsigned offset to 0x7fadfa73a800 overflowed to 0x7fa7fd501478 (stl_vector.h)

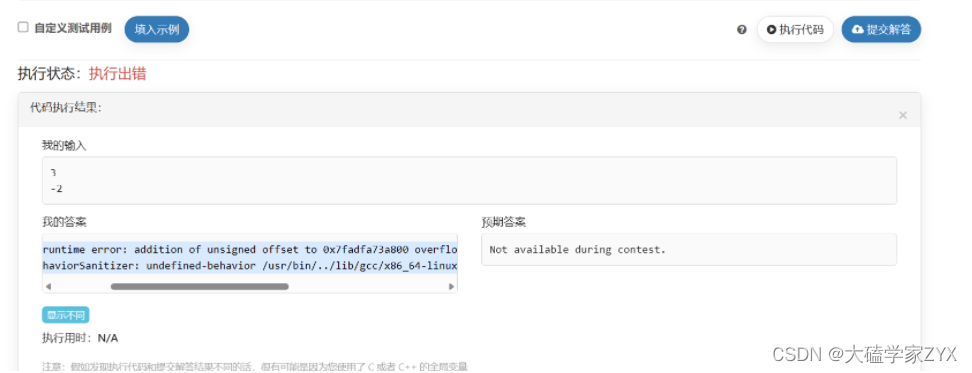
这个错误是由于内存溢出导致的。在我们的代码中，我们创建了一个非常大的动态规划数组 dp ，尺寸为 2 * MAX_VAL + 1 x MAX_N + 1，每个元素都是一个 int 类型。如果 MAX_VAL 和 MAX_N 都非常大，这个数组可能会超过可用的内存，从而导致程序崩溃。

实际上，我们不需要创建这么大的数组，因为我们的目标是找到最小的操作数，所以我们可以通过使用滚动数组或其他方式优化空间使用。不过这需要对代码做较大的修改，并且可能使代码变得更难理解。在这种情况下，可能更好的选择是使用其他算法或者优化我们的动态规划方法。

这道题比较困难现在还是没找到解决方法，后面学完了动规可以再来看看

左移报错：Line 19: Char 115: runtime error: left shift of negative value -62 (solution.cpp)

报错代码：

class Solution {
public:
    int makeTheIntegerZero(int num1, int num2) {
        const int MAX_N = 60;
        const int INF = 1e9;
        vector<vector<int>> dp(MAX_N + 1, vector<int>(2 * MAX_N + 1, INF));
        dp[0][MAX_N] = 0;

        for (int i = 0; i < MAX_N; ++i) {
            for (int j = -MAX_N; j <= MAX_N; ++j) {
                if (dp[i][j + MAX_N] == INF) {
                    continue;
                }
                for (int k = 0; k <= MAX_N; ++k) {
                    int nj = j - k;
                    if (nj < -MAX_N || nj > MAX_N) {
                        continue;
                    }
                    dp[i + 1][nj + MAX_N] = min(dp[i + 1][nj + MAX_N], dp[i][j + MAX_N] + (abs((1LL * (num2 + j)) << i) <= num1 ? 0 : 1));
                }
            }
        }
        
        int res = INF;
        for (int i = -MAX_N; i <= MAX_N; ++i) {
            res = min(res, dp[MAX_N][i + MAX_N]);
        }
        
        return res == INF ? -1 : res;
    }
};

在 C++ 中，移位操作的结果取决于其操作数的符号。对于负数的左移，C++ 并未定义行为，因此会导致报错。

报错中的"left shift of negative value -62"指的是在执行左移操作时，操作数为-62，因为在C++中，负数的左移是未定义的行为，所以编译器会报这个错误。

在这种情况下，我们应确保我们要左移的数是非负的。为了实现这一点，我们需要在进行位移操作前，先将 num2 + j 的绝对值转换为无符号整数。但是这还不够，因为我们可能需要对 num2 + j 的原始值进行一些操作，我们还需要存储它的符号。

整数溢出报错：Line 20: Char 75: runtime error: signed integer overflow: -9223372036854775808 * -1 cannot be represented in type ‘long long’ (solution.cpp)

此错误表示我们在尝试使用-9223372036854775808（也就是-2^63）乘以-1的时候发生了整数溢出，因为这个结果9223372036854775808大于long long型变量所能表示的最大值9223372036854775807。

为了解决这个问题，我们需要避免处理数值-9223372036854775808，即当计算得出的值val等于-9223372036854775808时，我们需要特殊处理。一种可能的解决方案是，当val等于-9223372036854775808时，我们假设结果为无穷大（或者一个大于结果可能范围的值），因为这样的数无法通过左移和加法变为0。

修改：

class Solution {
public:
    int makeTheIntegerZero(int num1, int num2) {
        const int MAX_N = 60;
        const int INF = 1e9;
        vector<vector<int>> dp(MAX_N + 1, vector<int>(2 * MAX_N + 1, INF));
        dp[0][MAX_N] = 0;

        for (int i = 0; i < MAX_N; ++i) {
            for (int j = -MAX_N; j <= MAX_N; ++j) {
                if (dp[i][j + MAX_N] == INF) {
                    continue;
                }
                for (int k = 0; k <= MAX_N; ++k) {
                    int nj = j - k;
                    if (nj < -MAX_N || nj > MAX_N) {
                        continue;
                    }
                    long long val = num2 + j;
                    if (val == -9223372036854775808LL) {
                        dp[i + 1][nj + MAX_N] = min(dp[i + 1][nj + MAX_N], INF);
                    } else {
                        long long shifted_val = ((val < 0 ? -val : val) << i) * (val < 0 ? -1 : 1);
                        dp[i + 1][nj + MAX_N] = min(dp[i + 1][nj + MAX_N], dp[i][j + MAX_N] + (abs(shifted_val) <= num1 ? 0 : 1));
                    }
                }
            }
        }

        int res = INF;
        for (int i = -MAX_N; i <= MAX_N; ++i) {
            res = min(res, dp[MAX_N][i + MAX_N]);
        }

        return res == INF ? -1 : res;
    }
};

但是这样做之后，还是有逻辑问题。这道题比较难可以后面学完了动规再回来看。