分类问题

准确率（Accuracy）

准确率是最简单也是最常用的分类指标之一。准确率指正确预测的样本数量占总样本数量的比例。准确率越高，说明模型的分类性能越好。
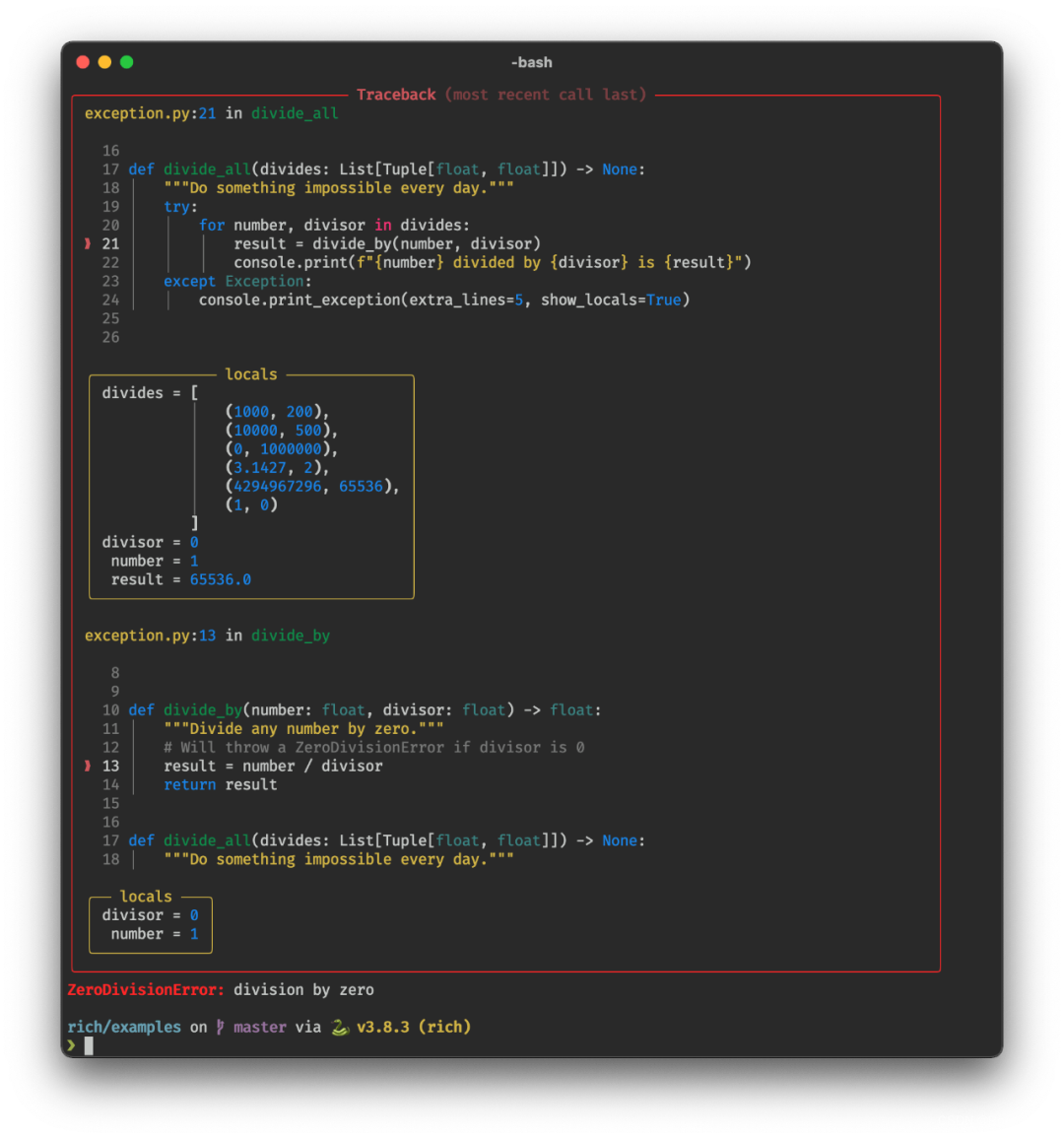
$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}$$
其中，$TP$表示真正例，即实际为正类且被预测为正类的样本数量；$TN$表示真负例，即实际为负类且被预测为负类的样本数量；$FP$表示假正例，即实际为负类但被预测为正类的样本数量；$FN$表示假负例，即实际为正类但被预测为负类的样本数量。

精确率（Precision）

精确率用于衡量模型预测为正类的样本中真正为正类的比例，即衡量模型的准确性。精确率越高，说明模型预测为正类的样本中真正为正类的比例越高。
$$Precision=\frac{TP}{TP+FP}$$

召回率或真正率（Recall）

召回率用于衡量所有实际为正类的样本中被模型预测为正类的比例（有效报警，灵敏度），即衡量模型的全面性。召回率越高，说明模型能够更好地发现正类样本。
$$Recall=\frac{TP}{TP+FN}$$

假正率（False Positive Rate, FPR）

所有负例中预测为正例的负例（误报，假阳性率）：
$$FPR=\frac{FP}{FP+TN}$$，
其中FP表示假正例，TN表示真反例。

特异性（Specificity）

是指在所有实际为负例的样本中，被正确预测为负例的比例。具体地，特异性可以用下面的公式计算：
$Specificity=\frac{TN}{TN+FP}$

ROC曲线

ROC曲线是一种衡量分类模型性能的图像化工具。ROC曲线的横轴是假正例率（FPR）也就是1-特异度，纵轴是真正例率（TPR），其形状可以反映出模型的性能。ROC曲线下面积（AUC）也是一种常用的分类指标，AUC越高，说明模型的性能越好。AUC的取值范围在0.5到1之间，AUC越接近1，分类器的性能越好。

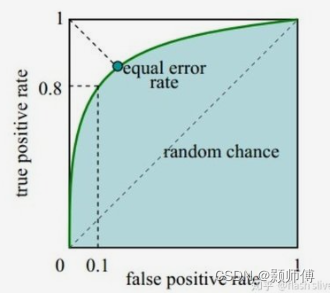
ROC曲线是通过改变分类模型的阈值（Threshold）来绘制的。分类模型的输出结果一般是一个连续的实数值，我们可以将这个值作为阈值，将样本分为正例和负例。当阈值为正无穷大时，所有样本都被判为负例；当阈值为负无穷大时，所有样本都被判为正例；当阈值为0时，所有样本都被判为正例。通过改变阈值，我们可以得到不同的FPR和TPR，从而绘制ROC曲线。

P-R曲线（精度-召回率曲线）

对于每个类别，按照置信度从高到低对预测框进行排序。

定义一系列阈值$[t_1,t_2,...,t_n]$，其中$t_1$为置信度最低的预测框的置信度，$t_n$为置信度最高的预测框的置信度。

对于每个阈值$t_i$，将置信度高于$t_i$的预测框视为正样本，低于$t_i$的预测框视为负样本。根据预测框与真实框之间的IoU值进行匹配，得到一组匹配的正样本和对应的IoU值。

计算该阈值下的精度和召回率，其中精度为与匹配的预测框的置信度相等，召回率为正样本的个数除以真实框的总数。

用所有阈值下的精度和召回率绘制精度-召回率曲线，即将精度作为横轴，召回率作为纵轴，每个点的坐标为$(P_i,R_i)$，其中$P_i$为召回率大于等于$t_i$时的精度，$R_i$为召回率大于等于$t_i$时的召回率。

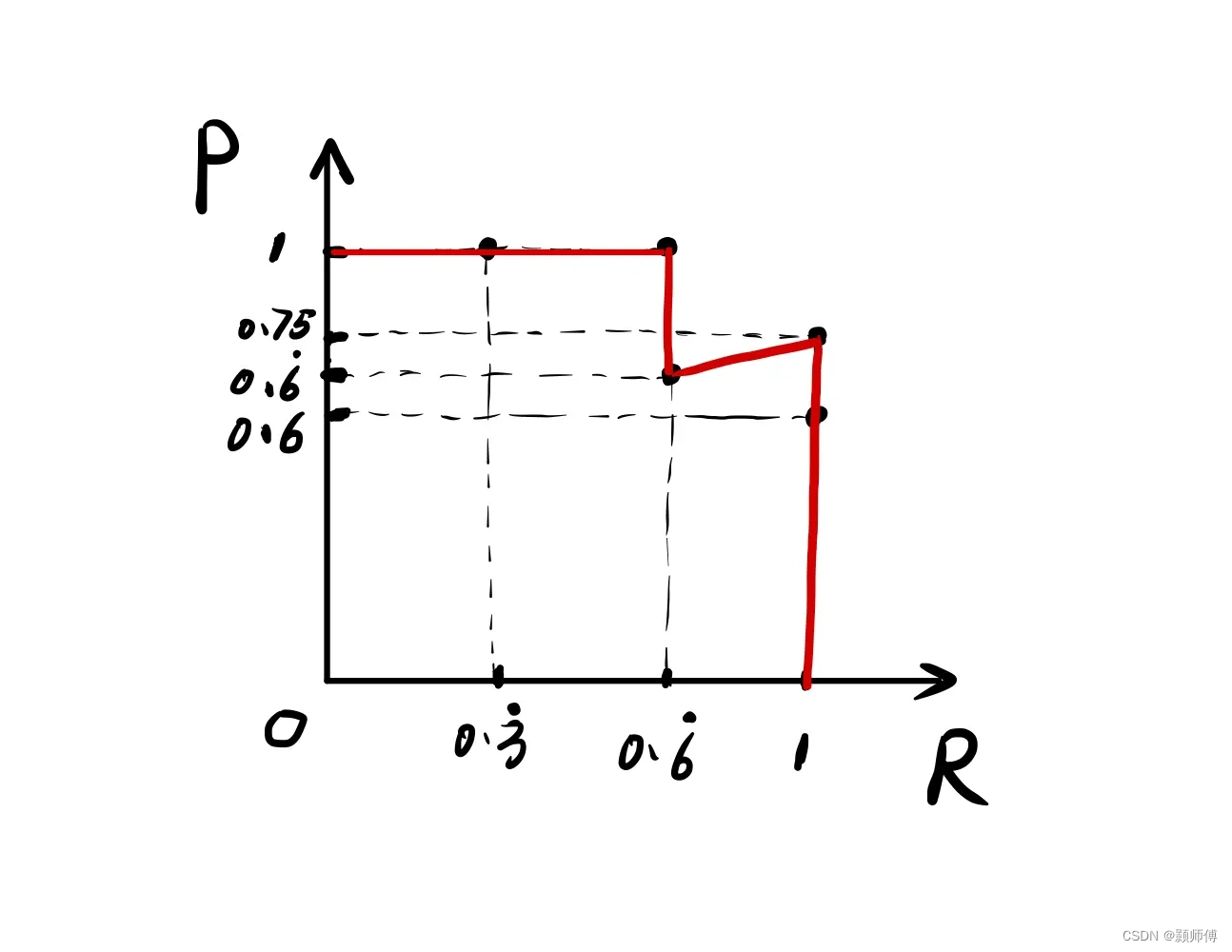
AP值

AP是对精度-召回率曲线下方面积的度量，表示了模型在所有召回率下的平均性能。计算AP时，我们需要根据精度-召回率曲线的形状，对曲线下方的面积进行积分。AP的取值范围是0到1之间，越接近1表示模型的性能越好。

MAP指标

我们以目标检测任务为例，假设我们的模型要对一张图片中的物体进行检测，图片中包含苹果、橙子、香蕉三种水果。我们用模型对这张图片进行检测后，得到了结果.

首先，我们将所有检测结果按照置信度从高到低排序，得到以下结果：
类别 置信度 边界框
苹果 0.8 (10, 10, 100, 100)
橙子 0.7 (20, 20, 120, 120)
苹果 0.6 (50, 50, 150, 150)
香蕉 0.5 (30, 30, 130, 130)
橙子 0.4 (60, 60, 160, 160)
然后，我们按照上述步骤计算每个类别的AP值。以苹果类别为例，我们可以得到以下精度-召回率表格：
置信度阈值 精度 召回率
0.4 0.5 1.0
0.6 0.67 0.67
0.8 1.0 0.67
根据这个表格，我们可以绘制出苹果类别的精度-召回率曲线，并计算出它的AP值。同样的方法，我们可以计算出橙子和香蕉类别的AP值。最后，将所有类别的AP值进行加权平均，就可以得到最终的mAP值。
在绘制AP曲线时，我们需要将所有类别的精度-召回率曲线绘制在同一张图中，以便进行比较。同时，我们也可以绘制不同IoU阈值下的AP曲线，以评估模型在不同IoU阈值下的性能表现。

在COCO数据集中的计算

在COCO数据集中，Map指标被广泛应用于目标检测和分割任务的评估中。COCO数据集是一个包含了80个不同类别的超过33万个标注框的大型数据集，因此在该数据集上进行目标检测和分割任务的评估非常有代表性。
COCO数据集中的Map指标计算方法和一般的Map指标计算方法略有不同，具体公式如下：
$$AP=\frac{1}{|R|}\sum _{i=1}^{|R|}{P}_i\Delta r_i$$
$$Map=\frac{1}{N}\sum _{i=1}^{N}A{P}_i$$
其中，$R$是所有真实标注框的集合，$N$是所有测试图片的数量。$A{P}_i$表示第$i$张测试图片的平均精度，通过计算该图片中所有物体类别的平均精度的平均值得到$Map$指标。$P_i$表示第$i$张测试图片所有物体类别的精度，$\Delta r_i$表示第$i$张测试图片中每个类别的召回率差异。

对于每张测试图片，需要计算出该图片中每个物体类别的平均精度（AP），然后将所有物体类别的平均精度的平均值作为该图片的平均精度。最终，将所有测试图片的平均精度取平均值，即为COCO数据集的Map指标。
在计算每个物体类别的平均精度时，需要考虑召回率的差异，即不同尺寸的物体对召回率的贡献不同。因此，COCO数据集中的Map指标会为不同大小的物体赋予不同的权重，以更准确地评估模型对于不同大小物体的检测和分割能力。
在实际应用中，可以使用一些开源的计算工具，如COCO API和mAP计算器等，来方便地计算COCO数据集中的Map指标。

F1值（F1-Score）

F1值是精确率和召回率的调和平均数，用于衡量模型的综合性能。F1值越高，说明模型的综合性能越好。
$$F1=2\frac{PrecisionRecall}{Precision+Recall}$$

调和平均数（Harmonic Mean）是统计学中的一种平均数，它的计算方法为n个数的倒数的平均数的倒数。具体地，n个正数 $x_1,x_2,...,x_n$ 的调和平均数可以表示为：
$$H=\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n}}=\frac{n}{{\sum }_{i=1}^n\frac{1}{x_i}}$$
与算术平均数、几何平均数和中位数等常见的平均数不同，调和平均数更加关注小数值，因为任何一个小于1的数的倒数都大于1，所以当一组数据中有个别数较小的时候，调和平均数会受到这些小数的影响而偏小。因此，调和平均数常用于一些需要考虑极端值的场合，例如计算速度、平均速率等。

什么时候用P-R曲线，什么时候用ROC曲线

P-R曲线和ROC曲线都是常用的分类模型性能评估指标，但是它们适用的场景不同。
P-R曲线主要用于正负样本比例不平衡的情况下，例如当正样本比例很低时。P-R曲线的横轴是召回率，纵轴是精确率，它反映了在不同召回率下，模型的分类性能表现。P-R曲线的优点是对于正样本的分类能力有更好的体现，尤其是当正样本比例较低时，可以反映出模型的性能差异。

ROC曲线则适用于正负样本比例相对平衡的情况下。ROC曲线的横轴是假正率（false positive rate），纵轴是真正率（true positive rate），它反映了在不同阈值下，模型的分类性能表现。在ROC曲线中，点（0,0）表示将所有样本都预测为负样本，点（1,1）表示将所有样本都预测为正样本，曲线越靠近左上角，表示模型的性能越好。

总的来说，当正负样本比例不平衡时，我们可以使用P-R曲线进行模型性能评估；当正负样本比例相对平衡时，我们可以使用ROC曲线进行模型性能评估。

混淆矩阵

混淆矩阵是一种将分类结果可视化的矩阵，它可以用于计算准确率、精确率、召回率等指标。混淆矩阵的行表示实际类别，列表示预测类别，矩阵中的每个元素表示实际类别和预测类别的交集数量。

回归问题

均方误差（MSE）
均方误差是回归问题中最常用的评价指标之一，它用于衡量模型预测值与真实值之间的差异。均方误差越小，说明模型的预测性能越好。
$$MSE=\frac{1}{n}\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2$$
其中，$n$表示样本数量，$y_i$表示第$i$个样本的真实值，$\widehat{y_i}$表示模型的预测值。

均方根误差（RMSE）
均方根误差是均方误差的平方根，它也用于衡量模型预测值与真实值之间的差异。均方根误差越小，说明模型的预测性能越好。
$$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2}$$

平均绝对误差（MAE）
平均绝对误差是回归问题中另一个常用的评价指标，它也用于衡量模型预测值与真实值之间的差异。平均绝对误差越小，说明模型的预测性能越好。
$$MAE=\frac{1}{n}\sum _{i=1}^n\left|y_i-\widehat{y_i}\right|$$