全文下载链接：http://tecdat.cn/?p=23287

在本文中，当从单变量波动率预测跳到多变量波动率预测时，我们需要明白，现在我们不仅要预测单变量波动率元素，还要预测协方差元素（点击文末“阅读原文”获取完整代码数据）。

相关视频

引言

假设你有两个序列，那么这个协方差元素就是2乘2方差-协方差矩阵的对角线。我们应该使用的准确术语是 "方差-协方差矩阵"，因为该矩阵由对角线上的方差元素和非对角线上的协方差元素组成。但是由于读 "方差-协方差矩阵 "非常累人，所以通常被称为协方差矩阵，或者有时不太正式地称为var-covar矩阵。

如果你还在读这篇文章，说明你在建立相关关系模型方面有一些经验。鉴于你知道各个序列的方差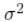，相关和协方差之间的联系是直接的。

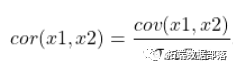
所以当我第一次研究这个问题时，我不明白为什么我们不单独建立所有非对角线的模型，例如使用样本成对相关的滚动窗口呢？你想有一个有效的相关矩阵，这意味着对称（很容易施加）和正负无限。

首先，为什么非负定属性很重要，其次，为什么它不容易施加。把非负定属性看作是多变量的，相当于单变量情况下对波动率的正向施加。你不会想让你的模型生成负的波动率吧？在单变量的情况下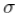，乘以任何平方数，我们都可以保持在正数的范围内。在更高的维度上，确保协方差的 "正性 "涉及到乘法，不是乘以一个平方的标量，而是乘以一个 "平方 "的矢量。

将XC表示为居中的随机变量X，所以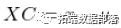。现在根据定义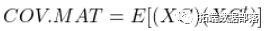是一个协方差矩阵，显然是非负定的。现在，如果我们用矩阵乘以一个 "平方 "向量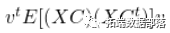，我们可以将向量 "插入 "期望值中（因为（1）向量不是随机变量，以及（2）期望算子的线性）。我们（应该）仍然得到非负定矩阵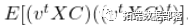。你用哪个向量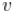并不重要，因为它是 "平方 "的。

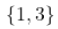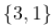如果我们对协方差条目进行单独建模，并将它们 "修补 "成一个矩阵，将每个成对的协方差放在正确的位置（例如，变量1和变量3之间的协方差在条目和，不能保证我们最终得到一个非负定的矩阵。由于不存在非负定的协方差矩阵，那么我们就有可能得到一个无效的协方差矩阵。

从业人员由于摆脱了繁琐的学术判断过程，可能会摆脱这个理论上的失误。然而，还有其他问题，在本质上是计算上的问题。一个非负的无限矩阵可以有零或负的行列式。在许多贝叶斯的应用中，我们希望使用精确矩阵而不是协方差矩阵。为了计算精确矩阵，我们简单地反转协方差矩阵，但这意味着我们要除以行列式，因此，行列式为零就会产生问题。

文献中的主要构建模块是GARCH过程。假设我们有一个随机变量，我们可以用它的波动率来建模。

(1)

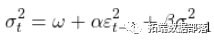
很容易理解。对于今天的波动率来说，重要的是昨天的波动率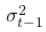，特别强调的是昨天的冲击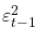，。请记住，如果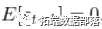，那么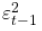仅仅是对方差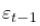的估计，而没有考虑到t-1以前的任何情况。

提高维度

现在，添加另一个随机变量。你现在有两个波动率和一个协方差项。但是，为什么不以向量自动回归（VAR）扩展自动回归的同样方式来扩展这个过程？进入VEC模型。

(2)

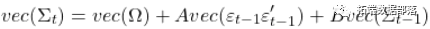
这里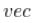是一个矢量化运算符，将一个矩阵作为一个矢量进行堆叠。由于矩阵的对称性，我们不需要所有的系数，所以更好的表述：

(3)

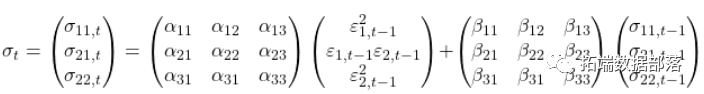
这个模型背后的直觉与VAR的基础是一样的。也许当股票的波动率高时，债券的波动率就低，也许当债券的波动率高时，与股票的协方差就高，等等。

这个模型的一个潜在问题，也是与VAR相似的，就是波动率是独立的过程，这意味着只有A和B的对角线是重要的，在这种情况下，我们只是用不必要的估计噪音来干扰这个模型。之前提到的另一个计算问题是，由于我们没有对矩阵过程本身进行建模，而是对三个项逐一进行建模，所以我们不能确保结果是一个有效的协方差矩阵，特别是没有施加非负-无限约束。BEKK模型（Baba, Engle, Kraft and Kroner, 1990）取得了这一进展。有一个很好的理由不详细讨论这些 "第一代 "模型。它们对于少数几个变量来说是非常难以估计的。我没有亲自尝试过那些模型。对于这些模型，即使人们成功地进行了估计，就实践者而言，估计的复杂性给结果带来了很大问题。

CCC 和DCC

恩格尔（2002）在其开创性的论文中提出了下一个重要的步骤，随后文献中出现了一个高潮。"Dynamic Conditional Correlation: 一类简单的多变量广义自回归条件异方差模型"。从摘要中可以看出："这些（模型）具有单变量GARCH模型的灵活性，加上参数化的相关模型"。这类条件相关模型的关键切入点是要认识到

(4)

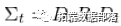
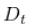是一个矩阵，对角线上是各个序列的波动率（现在单独估计），对角线外是零。这只是以矩阵形式对我们开始时的常规方程进行了处理。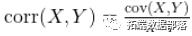，因为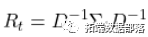。现在具备几个条件：

把对角线和非对角线分开，你可以用通常的单变量GARCH估计值来 "填补 "这个对角线。非对角线是由相关矩阵给出的，我们现在可以对其进行决定。当我们假设一个恒定的相关矩阵（CCC），也就是说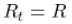，我们可以自然地使用样本相关矩阵。我们可以假设该矩阵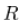是时变的，并使用滚动窗口或指数衰减权重或其他方式来估计它。
由于二次形式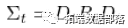，并且因为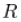是相关矩阵，我们肯定会得到一个有效的协方差矩阵，即使我们使用恒定的相关矩阵，它也是时间变化的。
由于这种对角线与非对角线的分离，我们实际上可以处理许多变量，与 "第一代 "类模型非常不同。我认为，这是该模型被接受和流行的主要原因。

现在我们进行估计。

使用R进行估算

让我们得到一些数据。我们提取三个ETF的过去几年的数据。SPY（追踪标准普尔500指数），TLT和IEF（分别追踪长期和中期债券）。

k <- 3 # 多少年数据
sym = c('SPY', 'TLT', "IEF") #  标准普尔500指数，长期和中期债券，所有ETFs
for (i in 1:l)getSymbols(sym\[i\], src="yahoo", from=start, to=end)
ret <- na.omit(ret)#  删除第一个观察值

现在来演示如何使用CCC和DCC模型构建协方差矩阵。我们首先得到单变量波动率。我们需要它们，它们位于对角线矩阵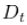的对角线上。我们用重尾的不对称GARCH来估计它们。

garch(distribution="std") #std是学生t分布

volatilityfit # 用一个矩阵来保存三种资产的波动率

for (i in 1:l) model = ugarchfit(spec,ret\[,i\])

现在，一旦我们有了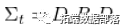，我们就能够创建基于CCC和DCC的协方差矩阵。对于CCC（恒定条件相关），我们使用样本相关矩阵，而对于DCC（动态），我们使用基于例如3个月的移动窗口估计的相关矩阵。

# 创建一个CCC模型的协方差

nassets <- l #  为了提高可读性，l看起来太像1了。

# 为不同时期的矩阵制作容器。

array(dim=c(n, nassets, TT))

# 计算样本无条件的相关矩阵。

samp_cor <- cor(ret) # 在整个循环过程中会保持不变

wind <- 60 # 大概三个月的时间

for (i in (w+1):TT)
(volatilitfit\[i,\])*diag(assets)
cov_ccc
cor_tv 
cov\_dcc<- dt %*% cor\_tv\[,,i\] %*% dt

结果

结果按年计算，并乘以100，转为百分比，以提高可读性。绘制它。

par()$mar # 边距

plot(ann*cov_ccc\[1,1,\]~time

plot(ann*cov_ccc\[1,2,\]~time)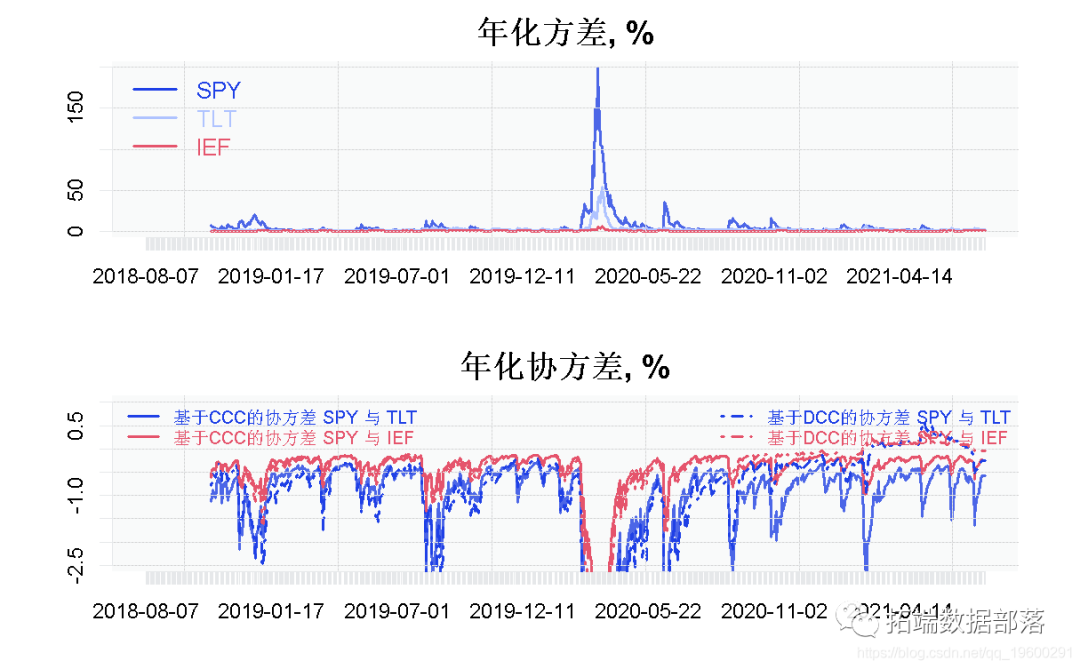

点击标题查阅往期内容

GARCH-DCC模型和DCC（MVT）建模估计

左右滑动查看更多

在上图中，我们有协方差矩阵的对角线。我们看到（1）中期债券的波动性最低，正如预期的那样，（2）SPY的波动性很大，方差也很高。(3) 曲线长端的方差高于中期的方差，这是收益率曲线文献中一个典型的事实。(4) 有趣的是，长期债券的波动性一直在上升，这可能是对即将提高政策利率的高度警觉。

在下图中，我们有三个协方差项，一次是假设CCC的估计（实线），一次是假设DCC的估计（虚线）。对于中期和长期债券之间的协方差，如果你假设恒定或动态相关矩阵，并不重要。然而，这对SPY与债券的协方差项确实很重要。例如，基于DCC的协方差矩阵认为在2013年中期股票和债券之间的协方差几乎为零，而基于CCC的协方差则表明在此期间的协方差为负。究竟是恒定的还是动态的，对跨资产投资组合的构建可能有很大的影响。