冒泡排序

思路：

1. 每次循环比较相邻两个元素，如果左边元素>右边元素，则交换位置。结果：将最大值放到最右边；
2. 一次循环过后，左边无序区域减少一个数，右边有序取增加一个数；
3. 序列长度为n，一共循环（n-1）次，并且 i 次循环需要比较（n-1-i）次。

评价：
时间复杂度
最坏情况： $O(n^2)$
平均情况：​​ $O(n^2)$
最好情况： $O(n^2)$

空间复杂度
所有情况：$O(1)$

稳定性：稳定。排序过程都是相邻的两位交换。

一次循环：

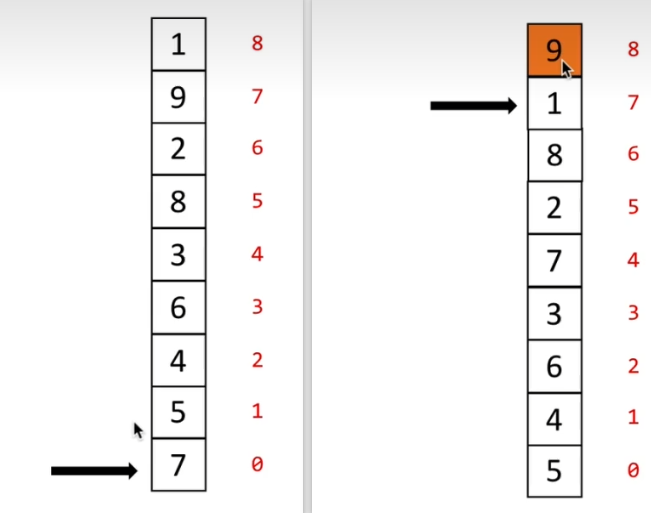
代码：

def bubble_sort(lst):
    """
    升序：每次循环把最大的数放到最右边
    优化：如果其中有一次循环没有发生任何交换，则提前结束
    """
    n = len(lst)
    # 外层循环控制比较的轮数
    for i in range(n - 1):
        exchange = False
        # 内层循环执行相邻元素的比较和交换
        for j in range(n - 1 - i):
            if lst[j] > lst[j + 1]:
                # 如果前面的元素大于后面的元素，进行交换
                lst[j], lst[j + 1] = lst[j + 1], lst[j]
                exchange = True
        print(lst)  # 打印每次循环的结果
        if not exchange:
            return

# 测试代码
numbers = [5, 8, 9, 1, 3]
print("最开始的数组为：\n", numbers)
bubble_sort(numbers)
print("经过排序后的数组为：\n", numbers)

选择排序

思路：

1. 每次循选择最小值放到最左边；
2. 一次循环过后，右边无序区域减少一个数，左边有序取增加一个数；
3. 序列长度为n，一共循环（n-1）次，每次从（i+1，n）中选择最小值。

评价：
时间复杂度
最坏情况： $O(n^2)$
平均情况：​​ $O(n^2)$
最好情况： $O(n^2)$

空间复杂度
所有情况：$O(1)$

稳定性：不稳定。排序过程不是相邻的两位交换。

代码：

def selection_sort(lst):
    """思路：每次循环找出最小值，并放到无序区的最左边"""
    n = len(lst)
    for i in range(n - 1):
        min_index = i
        for j in range(i + 1, n):
            if lst[j] < lst[min_index]:
                min_index = j
        lst[i], lst[min_index] = lst[min_index], lst[i]

# 测试代码
numbers = [5, 2, 9, 1, 3]
selection_sort(numbers)
print(numbers)

插入排序

思路：

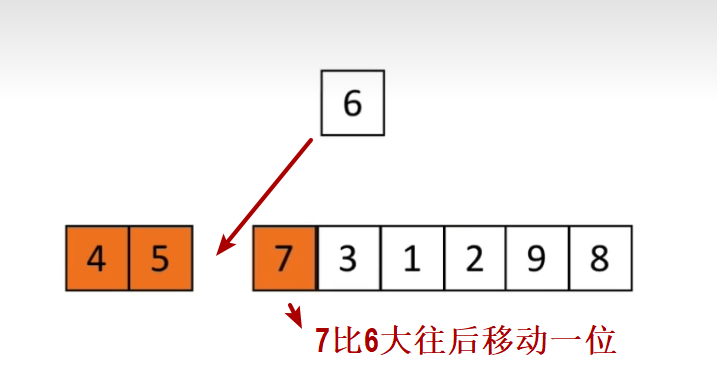
1. 类似于玩牌，初始时手里只有一张牌（将最左边第一个元素看作有序区）；
2. 每次从右边无序区拿第一个元素，放到有序区（循环与有序区右边比较，有序区元素大则往后移动）；
3. 序列长度为n，循环摸牌（1，n）位置的无序牌。

评价：
时间复杂度
最坏情况： $O(n^2)$
平均情况：​​ $O(n^2)$
最好情况： $O(n^2)$

空间复杂度
所有情况：$O(1)$

稳定性：稳定。排序过程没有不相邻的元素对位交换。

循环前：

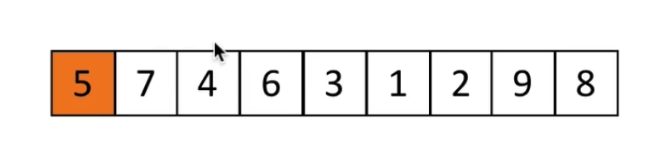
循环过程中：

代码：

def insertion_sort(lst):
    for i in range(1, len(lst)):
        key = lst[i]  # 摸牌
        j = i - 1  # j是有序区最大的牌的index
        # 如果有序区的牌比摸到的牌大，往后移动一位
        while j >= 0 and lst[j] > key:
            lst[j + 1] = lst[j]
            j -= 1
        # 循环结束找到了摸到牌正确的插入位置
        lst[j + 1] = key


# 测试代码
numbers = [5, 2, 9, 1, 3]
insertion_sort(numbers)
print(numbers)