目录
- 一、栈在括号匹配中的应用
- 逻辑实现
- 代码实现
- 二、栈在表达式求值中的应用
- 手算实现
- 代码实现
- 三、栈在递归中的应用
- 逻辑实现
- 代码实现
一、栈在括号匹配中的应用
括号匹配,顾名思义。若括号按照正确的格式嵌套,则可正确匹配,例如([]),反之若括号按照不正确的格式嵌套,则不可正确匹配,例如([))。
逻辑实现
考虑下列括号序列:
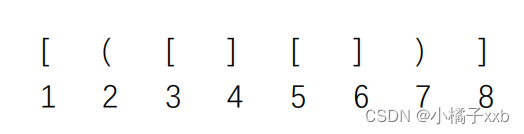
分析该括号序列是否可正确匹配的流程如下:
1、接收第1个括号"[“后,期待与之匹配的第8个括号”]“出现
2、接收第2个括号”(“,此时第1个括号”[“暂时放在一边,期待与之匹配的第7个括号”)“出现
3、接收第3个括号”[“,此时第2个括号”(“暂时放在一边,期待与之匹配的第4个括号”]“出现
4、接收第4个括号”]",第3个括号的期待得到满足,等待第2个括号的期待出现
5、以此类推
代码实现
算法思想:
1、初始时设置一个空栈,顺序读入等待判断的括号序列
2、若读入的是右括号,有两种情况:第一种情况是使置于栈顶的最急迫的期待得以满足,第二种情况为不合法(括号序列不匹配,退出程序)
3、若读入的是左括号,则作为一个急迫的期待压入栈中(后压入的期待比先压入的期待更加急迫)
4、若算法结束时栈为空,则匹配成功,否则,匹配失败
代码如下:
int Parentheses_match(char Arr,int n){//要判断的括号序列存储在数组Arr[n]中
SqStack S;
InitStack(&S);//初始化栈
int i=0;
for(i=0;i<n;i++){//读取括号序列
if(Arr[i]=='('||Arr[i]=='[') Push(&S,Arr[i]);//若读入的是左括号,入栈
else if(Arr[i]==')'||Arr[i]==']'){//若读入的是右括号
char x;
GetTop(S,&x);//读栈顶元素,并用x返回栈顶元素
//判断右括号是否和栈顶的左括号匹配
if((x=='('&&Arr[i]==')')||(x=='['&&Arr[i]==']')){
Pop(&S,&x);//弹出栈顶元素,等待下个期待被满足
};//满足左括号的期待
else return 0;//右括号未和最近的左括号配对,序列不合法
}
}
if(StackEmpty(S)) return 1;//读取完括号序列后栈为空,序列合法
else return 0;
}
其中用到的栈的基本操作可见文章操作受限的线性表——栈
二、栈在表达式求值中的应用
我们平时见到的表达式都是从左往后理解的,例如a+b=c、a/b=c等,我们可以称这种阅读方式为中缀表达式(即运算符在两个运算数中间)。相对应的是后缀表达式(即运算符在两个运算数之后)。
手算实现
例如,中缀表达式
A
+
B
∗
(
C
−
D
)
−
E
/
F
A+B*(C-D)-E/F
A+B∗(C−D)−E/F对应的后缀表达式为
A
B
C
D
−
∗
+
E
F
/
−
ABCD-*+EF/-
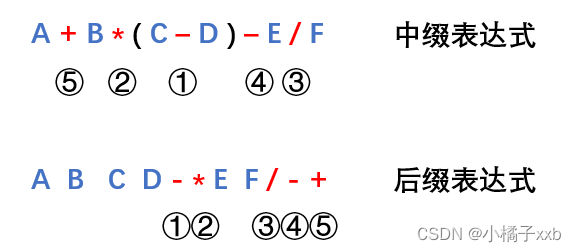
ABCD−∗+EF/−中缀表达式转换为后缀表达式的过程如下图所示(按照运算符的运算顺序进行转换):

需要注意的是,中缀表达式转化为后缀表达式的结果并不唯一,例如下图也是一种转化方式。这种不唯一性来源于某些运算的优先级相同,例如’+‘和’-‘,’*‘和’/'。我们在进行中缀表达式和后缀表达式的转换时,往往采用上图的转换原则——优先级相同的运算符从左到右进行编号。
代码实现
算法思想:
1、顺序扫描表达式的每一项,根据类型做如下操作
2、若该项是操作数,则将其压入栈中
3、若该项是操作符(简写为op),则连续从栈中退出两个操作数Y和X,形成运算指令XY,并将得到的结果重新压入栈中
4、当表达式的所有项都扫描处理完后,栈顶存放的就是最后的计算结果
代码如下:
int Expression_evaluation(char Arr,int n){//表达式存储在Arr数组中
SqStack S;
InitStack(&S);//初始化栈
int i=0;
for(i=0;i<n;i++){//读取表达式
if(Arr[i]>=48&&Arr[i]<=57) Push(&S,Arr[i]);//读取的是操作数,入栈
else{//读取的是操作符,出栈两个操作数进行运算
int x;
int y;
if(Arr[i]==42){//如果是乘法运算
Pop(&S,&x);
Pop(&S,&y);
x=x*y;
Push(&S,x);
}
else if(Arr[i]==47){//如果是除法运算
Pop(&S,&x);
Pop(&S,&y);
x=x/y;
Push(&S,x);
}
else if(Arr[i]==43){//如果是加法运算
Pop(&S,&x);
Pop(&S,&y);
x=x+y;
Push(&S,x);
}
else if(Arr[i]==45){//如果是减法运算
Pop(&S,&x);
Pop(&S,&y);
x=x-y;
Push(&S,x);
}
else return -10000;//返回-10000表示表达式格式不正确
}
}
int answer=GetTop(S,&x);//栈顶元素为计算结果
return answer;
}
三、栈在递归中的应用
递归可以理解为一个函数/过程/数据结构的定义中又应用了它自身,则这个函数/过程/数据结构是递归定义的,简称递归。
递归模型必须满足两个条件,第一通过循环体(递归表达式)实现递归,第二递归要有出口(结束条件)。
一个典型的递归的例子是斐波那契数列:
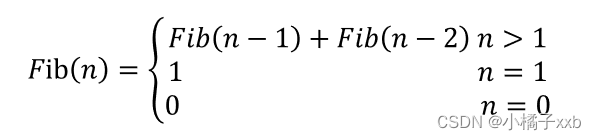
代码实现如下:
int Fib(int n){
if(n==0) return 0;
else if(n==1) return 1;
else return Fib(n-1)+Fib(n-2);//递归表达式
}
在递归调用的过程中,系统为每一层的返回点、局部变量、传入实参等开辟了递归工作栈来进行数据存储(函数调用时,需要用一个栈存储调用的返回地址、实参和局部变量等)。若递归的次数过多,容易造成栈溢出。
递归的有点事代码简单且容易理解,但效率不高,因为其包含很多重复的计算,例如在计算Fib(5)时,要先计算Fib(4)和Fib(3),在计算Fib(4)时又要计算Fib(3)和Fib(2)… …一共需要计算2次Fib(3)、3次Fib(2),5次Fib(1)和3次Fib(0)。
逻辑实现
如果想把递归算法转换为非递归算法,就需要借助栈来实现。例如斐波那契数列,在每一次计算时,都从栈顶读取(注意使读值不是出栈)两个元素相加再入栈,即可得到每一个斐波那契数列。
代码实现
int Fib_stack(int n){//计算Fib(n)
if(n=0) return 0;//Fib(0)
else if(n=1) return 1;//Fib(1)
else{//Fib(n) n>1
SqStack S;
InitStack(&S);//初始化栈
int F0=0;
int F1=1;
Push(&S,F0);//Fib(0)入栈
Push(&S,F1);//Fib(1)入栈
int i=0;
int Fi;
int Fj;
int Fk;
for(i=2;i<=n;i++){//非递归的计算Fib(i)
GetTop(S,&Fj);
GetSecond(S,&Fk);
Fi=Fj+Fk;
Push(&S,Fi);
}
}
int Fn;
GetTop(S,&Fn);
if(i==n) return Fn;//返回Fib(n)
}
另有队列的应用——层次遍历、计算机系统文章见链接【待补充】
本文内容为个人学习总结所得,如有问题欢迎评论区提出。