---

【可更换其他算法，获取资源请见文章第5节：资源获取】

---

1. 原始COA算法

长鼻浣熊优化算法（Cоati Optimization Algorithm，COA）是一种启发式优化算法，灵感来源于长鼻浣熊（Coati）的行为策略。长鼻浣熊优化算法基于长鼻浣熊在觅食过程中的特性和行为模式。长鼻浣熊是一种树栖动物，具有长而灵活的鼻子，用于觅食和捕食。它们通过嗅觉感知周围环境，利用敏锐的视觉和协调的运动能力来寻找食物。

1.1 开发阶段

这个阶段模拟的是浣熊对鬣蜥的攻击策略，对搜索空间中的种群更新的第一个阶段进行建模。在这个策略中，一群浣熊会爬上树，对着一只鬣蜥，并吓唬它，其他几个浣熊会在树下等待鬣蜥掉下来。当鬣蜥掉下来之后，浣熊就会攻击并猎杀它。这个策略使得COA在搜索空间中移动到不同的位置，说明COA在问题解决空间中的全局搜索能力。

在COA的设计中，种群中的最佳位置被假定为鬣蜥的位置。此外，还假设有一般的浣熊能爬上树，另一半在地上等待鬣蜥掉下来。因此，浣熊在树上的位置可以用以下公式描述：

鬣蜥落地后，将其放置在搜索空间中的任意位置。基于这种随机位置，地面上的浣熊可以在搜索空间中移动，用下列公式来描述：

对于每个浣熊计算的新位置，如果它改善了目标函数的值，那么就会被接受，否则，浣熊将保持原先的位置，此过程用以下公式来表示。这个可以被视为贪婪法则。

这里$x_i^{P1}$是计算第$i$个浣熊的新位置，$x_{i,j}^{P1}$是它的第$j$维，$F_i^{P1}$是它的目标函数值，$r$是$[0,1]$区间内的随机实数。$Iguana$代表鬣蜥在搜索空间中的位置，这实际上是指种群中最佳个体的位置；$Iguan{a}_j$是它的第$j$维，$j$是一个整数，从集合{1,2}中随机选择，$Iguan{a}^G$是在地面上的位置，它是随机生成的。$Iguan{a}_j^G$蠢晰是它的第$j$维，$F_{Iguana}^G$是它的目标函数值。

1.2 探索阶段

在第二阶段即探索阶段的过程中，位置更新模拟的是浣熊在遇到捕食者和逃避捕食者的行为。当食肉动物攻击浣熊时，浣熊就会从它的位置上逃走。浣熊在该策略中的移动使其处于接近其当前位置的安全位置，这代表这COA的局部开发能力。为了模拟这种行为，COA在每个长鼻浣熊个体附近生成一个随机位置，公式如下所示：

与开发阶段中类似，同样使用贪婪选择来决定是替换还是保留原先的位置。

2. 工程应用问题优化

程序共包含压力容器设计、滚动轴承设计、拉压弹簧设计、悬臂梁设计和轮系设计共5种工程应用问题，下面详细介绍了其中两种工程应用问题。

2.1 压力容器设计

2.2 拉压弹簧设计

拉压弹簧设计问题优化目标是使下图所示的拉伸/压缩弹簧的质量最小化。

该问题需要在满足剪切力、挠度、波动频率、外径等约束条件下进行求解。该问题中有3个设计变量，分别为线圈直径d、平均线圈直径D和线圈数量N。该问题数学模型如下所示：

3. 部分代码展示

    %----------------------------------------------------------------------
    %%% (COA) for 5 engineering designs %%%
    % ---------------------------------------------------------------------
    %%%%%%%%%%% Engineering lists %%%%%%%%%%%%%%
    %  1.Pressure vessel design                %
    %  2.Rolling element bearing design        %
    %  3.Tension/compression spring design     %
    %  4.Cantilever beam design                %
    %  5.Gear train design                     %
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    % BestX:The best solution                  %
    % BestF:The best fitness                   %
    % HisBestF:History of the best fitness     %
    % EngIndex:index of engineerings           %
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    clc;
    clear;
    close all;
    
    EngList=[{'Pressure vessel design'},...
             {'Rolling element bearing design'},...
             {'Tension/compression spring design'},...
             {'Cantilever beam design'},...
             {'Gear train design'}];
    MaxIteration=500;
    PopSize=30;
    
    EngIndex=5; % 切换数字：1=压力容器设计问题 2=滚动轴承设计问题 3=压缩弹簧设计问题 4=悬臂梁设计问题 5=轮系设计问题
    
    [BestX,BestF,HisBestF]=COA(EngIndex,MaxIteration,PopSize);
    if EngIndex==2 || EngIndex==3
        BestX(3)=round(BestX(3));
    elseif  EngIndex==5
        BestX=round(BestX);
    end
    
    display(['The best fitness of ',EngList{EngIndex},' is: ', num2str(BestF)]);
    display(['The best solution is: ', regexprep(num2str(BestX),'\s*',',')]);
    figure;
    if BestF>0
        semilogy(HisBestF,'r','LineWidth',2);
    else
        plot(HisBestF,'r','LineWidth',2);
    end
    
    xlabel('Iterations');
    ylabel('Fitness');
    title([EngList{EngIndex}]);

4. 仿真结果展示

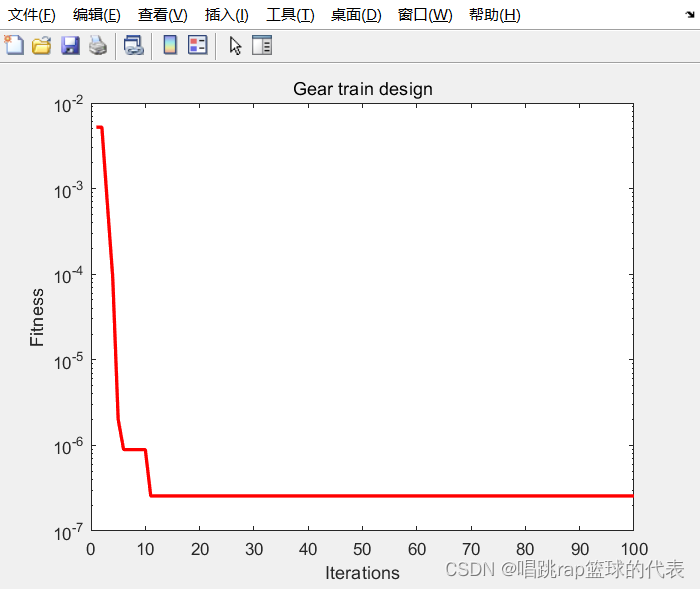
5. 资源获取

可以获取完整代码资源，可以更换其他算法。