题目来源
2287 -- Tian Ji -- The Horse Racing (poj.org)
题目描述
田忌赛马是中国历史上一个著名的故事。
这个故事发生在2300年前,田忌是齐国的一个大官,他喜欢和齐王以及其他公子赛马。
田忌和齐王都有三类马,分别是下等马,中等马,上等马。
比赛一共进行三轮,每匹马只能在某一轮比赛中使用。每一轮的胜者可以从败者获得200银币。
齐王是齐国最有权势的人,因此他的马都非常好,每个级别的马都要比田忌的同级别的马更好。因此,田忌每次都会输600银币给齐王。
田忌为此非常苦恼,直到他遇见了孙膑,这个中国历史上最有名的军师之一。孙膑为田忌提供了如下策略,让田忌在接下来的比赛中赢回了200银币。这是一个非常简单的策略,即:
- 田忌的下等马 vs 国君的上等马(田忌输,失去200银币)
- 田忌的中等马 vs 国君的下等马(田忌赢,获得200银币)
- 田忌的上等马 vs 国君的中等马(田忌赢,获得200银币)
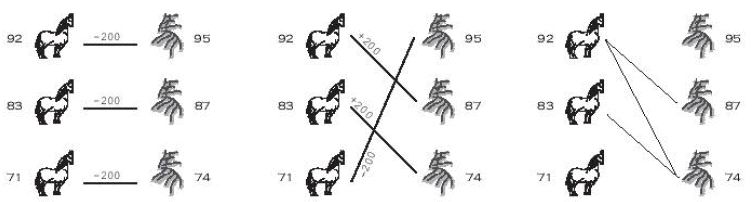
其实上面的赛马问题可以简单地看成是:二分图中寻找最大匹配。
把田忌的马画在一遍,把齐王的马画在另一边。
田忌的马只要能战胜齐王的马,我们就在这两匹马之间画一道连接线,表示我们希望让这两匹马进行匹配比赛。
那么,田忌赢得尽可能多的回合,其实就是在这个图中找到最大匹配。
如果存在平手,那么问题就会变得更佳复杂,他需要为所有可能的变分配权重0、1或-1,并找到一个最大的加权完美匹配。
然后,赛马问题是一个非常特殊的二分图匹配问题。这张图是由马的速度决定的。速度较快的顶点总是胜过速度较慢的顶点。在这种情况下,加权二分图匹配算法显得有点大材小用了。
请你设计一个算法来解决这种特殊匹配问题。
输入描述
最多输入50组用例。
每组用例:
- 第一行为一个整数n(n ≤ 100)表示每一方马的数量。
- 第二行为n个整数,表示田忌的马的速度。
- 第三行为n个整数,表示齐王的马的速度。
输入的结束条件是,在最后一组用例之后输入只有'0'的一行。
输出描述
对每组用例输出一行,每行包含一个整数,表示该组用例下,田忌所能获得最大银币数。
用例
| 输入 | 3 92 83 71 95 87 74 2 20 20 20 20 2 20 19 22 18 0 |
| 输出 | 200 0 0 |
| 说明 | 无 |
题目解析
本题可以使用贪心思维去解决问题。
即:要想田忌获得银币最多,则应该让田忌输的最少,那么如何让田忌输的最少呢?
那就是用田忌 "必输的" 且 "最慢的" 马 去消耗掉 齐王最快的马。
因此,我们需要先将田忌和齐王的马进行升序,这样就能找到最慢和最快的马。
- 如果田忌最快的马 > 齐王最快的马,则此轮田忌胜出
- 如果田忌最快的马 < 齐王最快的马,则此轮田忌必输,但是为了保留住田忌最快的马,我们应该让田忌把最慢的马拿出来比赛,这样就会以最小代价输。
- 如果条件最快的马 == 齐王最快的马,则此轮田忌平局,但是代价确实失去了最快的马,此时我们应该考虑从田忌的马中,找到一匹必输的、且最慢的马的去消耗掉齐王的最快的马,这样虽然此轮输了,但是田忌只是将必输的那匹马提前输了而已,好处是,保留住了最快的马。因此接下来我们应该找到田忌必输的,且最慢的马。
- 如果田忌最慢的马 > 齐王最慢的马,则当前田忌最慢的马不是田忌必输的、最慢的马,我们应该继续寻找
- 如果田忌最慢的马 < 齐王最慢的马,则当前田忌最慢的马就是田忌必输的、且最慢的马,我们应该拿这匹马和齐王最快的马比赛
- 如果田忌最慢的马 == 齐王最慢的马,则当前田忌最慢的马不是田忌必输的且最慢的马,我们应该继续寻找
JS算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
if (line == "0") {
const cases = [];
for (let i = 0; i < lines.length; i += 3) {
const n = parseInt(lines[i]);
const a = lines[i + 1].split(" ").map(Number); // 田忌的马速度数组
const b = lines[i + 2].split(" ").map(Number); // 齐王的马速度数组
cases.push([n, a, b]);
}
getResult(cases);
lines.length = 0;
} else {
lines.push(line);
}
});
function getResult(cases) {
for (let c of cases) {
const n = c[0];
const a = c[1];
const b = c[2];
a.sort((a, b) => a - b);
b.sort((a, b) => a - b);
let la = 0; // 指向田忌最慢的马
let ra = n - 1; // 指向田忌最快的马
let lb = 0; // 指向齐王最慢的马
let rb = n - 1; // 指向齐王最快的马
let ans = 0; // 记录田忌获得银币数
while (la <= ra) {
if (a[ra] > b[rb]) {
// 田忌最快的马 比 齐王最快的马要快, 则直接比
ans += 200;
ra--;
rb--;
} else if (a[ra] < b[rb]) {
// 田忌最快的马 比 齐王最快的马要慢, 则结果肯定输, 为了保留田忌最快的马, 我们应该用田忌最慢的马去消耗掉齐王最快的马
ans -= 200;
la++;
rb--;
} else {
// 田忌最快的马 和 齐王最快的 速度相同, 此时如果平局的话,则会让田忌损失最快的马,因此我们应该找到田忌最慢的马, 即田忌必输的马来消耗掉齐王最快的马
if (a[la] > b[lb]) {
// 如果田忌最慢的马 比 齐王最慢的马 快, 则此时田忌最慢的马不是必输的马
ans += 200;
la++;
lb++;
} else {
// 如果田忌最慢的马速度 <= 齐王最慢的马速度, 此时应该让田忌最慢的马 去消耗 齐王最快的马
// 如果齐王最快的马速度 > 田忌最慢的马速度,则田忌失去银币
// 如果齐王最快的马速度 == 田忌最慢的马速度,则田忌不失去银币
if (b[rb] > a[la]) ans -= 200;
la++;
rb--;
}
}
}
console.log(ans);
}
}
Java算法源码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static class Case {
int n;
int[] a; // 田忌的马速度数组
int[] b; // 齐王的马速度数组
public Case(int n, int[] a, int[] b) {
this.n = n;
this.a = a;
this.b = b;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
ArrayList<Case> cases = new ArrayList<>();
// POJ Java只支持jdk1.5, 因此如果需要在POJ验证的话,需要替换为下面更低级的语法
// ArrayList cases = new ArrayList();
while (true) {
String line = sc.next();
if ("0".equals(line)) {
getResult(cases);
break;
} else {
int n = Integer.parseInt(line);
int[] a = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
int[] b = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
// POJ Java只支持jdk1.5, 因此如果需要在POJ验证的话,需要替换为下面更低级的语法
// int[] a = new int[n];
// for (int i = 0; i < n; i++) a[i] = Integer.parseInt(sc.next());
//
// int[] b = new int[n];
// for (int i = 0; i < n; i++) b[i] = Integer.parseInt(sc.next());
cases.add(new Case(n, a, b));
}
}
}
public static void getResult(ArrayList<Case> cases) {
for (Case c : cases) {
int n = c.n;
int[] a = c.a;
int[] b = c.b;
Arrays.sort(a);
Arrays.sort(b);
int la = 0; // 指向田忌最慢的马
int ra = n - 1; // 指向田忌最快的马
int lb = 0; // 指向齐王最慢的马
int rb = n - 1; // 指向齐王最快的马
int ans = 0; // 记录田忌获得银币数
while (la <= ra) {
if (a[ra] > b[rb]) {
// 田忌最快的马 比 齐王最快的马要快, 则直接比
ans += 200;
ra--;
rb--;
} else if (a[ra] < b[rb]) {
// 田忌最快的马 比 齐王最快的马要慢, 则结果肯定输, 为了保留田忌最快的马, 我们应该用田忌最慢的马去消耗掉齐王最快的马
ans -= 200;
la++;
rb--;
} else {
// 田忌最快的马 和 齐王最快的 速度相同, 此时如果平局的话,则会让田忌损失最快的马,因此我们应该找到田忌最慢的马, 即田忌必输的马来消耗掉齐王最快的马
if (a[la] > b[lb]) {
// 如果田忌最慢的马 比 齐王最慢的马 快, 则此时田忌最慢的马不是必输的马
ans += 200;
la++;
lb++;
} else {
// 如果田忌最慢的马速度 <= 齐王最慢的马速度, 此时应该让田忌最慢的马 去消耗 齐王最快的马
// 如果齐王最快的马速度 > 田忌最慢的马速度,则田忌失去银币
// 如果齐王最快的马速度 == 田忌最慢的马速度,则田忌不失去银币
if (b[rb] > a[la]) ans -= 200;
la++;
rb--;
}
}
}
System.out.println(ans);
}
}
}
Python算法源码
# 算法入口
def getResult(cases):
for case in cases:
n = case[0]
a = case[1]
b = case[2]
a.sort()
b.sort()
la = 0 # 指向田忌最慢的马
ra = n - 1 # 指向田忌最快的马
lb = 0 # 指向齐王最慢的马
rb = n - 1 # 指向齐王最快的马
ans = 0 # 记录田忌获得银币数
while la <= ra:
if a[ra] > b[rb]:
# 田忌最快的马 比 齐王最快的马要快, 则直接比
ans += 200
ra -= 1
rb -= 1
elif a[ra] < b[rb]:
# 田忌最快的马 比 齐王最快的马要慢, 则结果肯定输, 为了保留田忌最快的马, 我们应该用田忌最慢的马去消耗掉齐王最快的马
ans -= 200
la += 1
rb -= 1
else:
# 田忌最快的马 和 齐王最快的 速度相同, 此时如果平局的话,则会让田忌损失最快的马,因此我们应该找到田忌最慢的马, 即田忌必输的马来消耗掉齐王最快的马
if a[la] > b[lb]:
# 如果田忌最慢的马 比 齐王最慢的马 快, 则此时田忌最慢的马不是必输的马
ans += 200
la += 1
lb += 1
else:
# 如果田忌最慢的马速度 <= 齐王最慢的马速度, 此时应该让田忌最慢的马 去消耗 齐王最快的马
# 如果齐王最快的马速度 > 田忌最慢的马速度,则田忌失去银币
# 如果齐王最快的马速度 == 田忌最慢的马速度,则田忌不失去银币
if b[rb] > a[la]:
ans -= 200
la += 1
rb -= 1
print(ans)
# 输入获取
cases = []
while True:
line = input()
if line == "0":
# 算法调用
getResult(cases)
break
else:
n = int(line)
a = list(map(int, input().split())) # 田忌的马速度数组
b = list(map(int, input().split())) # 齐王的马速度数组
cases.append([n, a, b])