Q-learning算法介绍

在本节课程的第一单元中，我们已经学习了强化学习、强化学习训练过程以及不同的解决强化学习的方法。我们还训练了第一个智能体并将其上传到了HuggingFace社区。

在本单元，我们将更深入的学习一种强化学习的方法：基于价值的方法，并开始学习第一个强化学习算法：Q-Learning算法。

我们还会从零开始实现第一个Q-learning强化学习智能体，并在两个环境中训练它。

1. Frozen-Lake-v1 (不打滑的版本): 在这里我们的智能体需要通过在冰面(F)上行走并躲避冰坑(H)，使其从初始状态(S)到目标状态(G)。
2. 自动摩的：在这里我们的智能体需要学习在城市中行驶从而把乘客从点A送到点B。

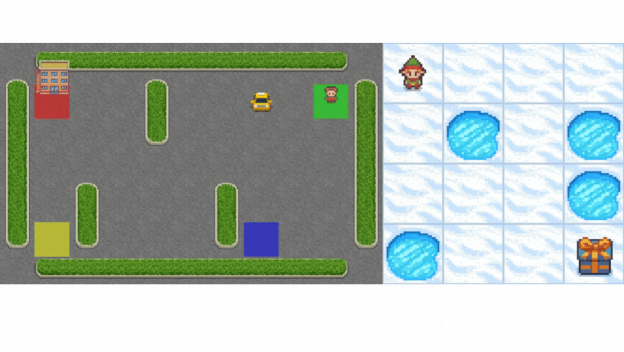
我们具体要学习以下内容：

• 学习基于价值的方法。
• 了解蒙特卡洛和时序差分学习之间的区别。
• 理解并实现我们的第一个强化学习算法：Q-learning。

如果你想要进一步学习Deep Q-learning算法，那一定要重视本单元的基础学习。Deep Q-learning是第一个在部分Atari游戏上（如breakout, 太空入侵者等）表现超过人类的深度强化学习算法。

现在让我们开始吧！🚀

回顾: 什么是RL?

在强化学习中，我们构建一个能做智能决策的智能体。例如，一个学习玩电子游戏的智能体，或一个能够通过决定商品的购入种类和售出时间从而最大化收益的贸易智能体。

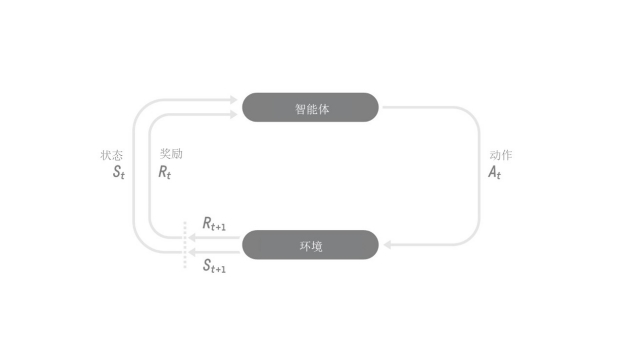
但是为了做出比较聪明的决策，我们的智能体需要通过反复试验与环境交互并接受奖励（正向或负向）作为唯一反馈，以此进行学习。

智能体的目标是最大化累计期望奖励（基于奖励假设）

智能体的决策过程称作策略π：给定一个状态，一个策略将输出一个动作或一个动作的概率分布。也就是说，给定一个环境的观察，策略将会输出一个行动（或每一个动作的概率），智能体将会执行该动作。

我们的目标是找到一个最优的策略π*，也就是一个能够获得最好的累计期望奖励的策略。

并找到这个最优策略（为解决强化学习问题），有两种主要的强化学习方法：

• 基于策略的方法：根据给定的状态直接训练智能体学习要执行的动作。
• 基于价值的方法：训练一个价值函数来学习更具有价值的状态，并用这个价值函数采取能够获得更有价值状态的动作。

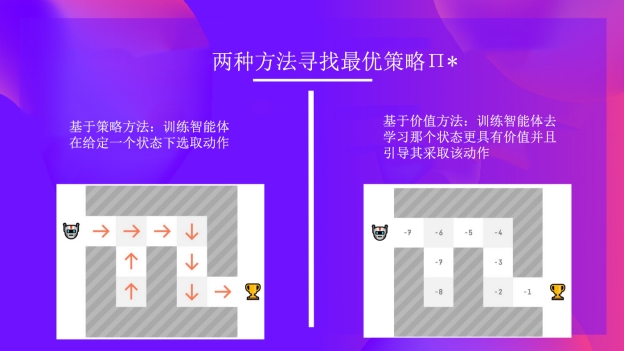
在本单元中，我们将深入学习基于价值的方法。

两种基于价值的方法

在基于价值的方法中，我们将学习一个价值函数，该价值函数可以估算在某个状态下所能获得的预期回报，即它将一个状态映射到处于该状态的期望值。

一个状态的价值是智能体按照给定策略，从当前状态开始行动所能获得的预期折扣回报。

按照给定策略行动是什么意思呢？因为在基于价值的方法中没有策略，我们训练的是价值函数，而不是策略。

要记得智能体的目标是有一个最优策略π*。

为了找到最优策略，我们使用两种不同的方法进行学习：

• 基于策略的方法： 直接训练策略，以选择在给定状态下采取的动作（或者在该状态下的动作概率分布）。在这种情况下，我们没有价值函数。

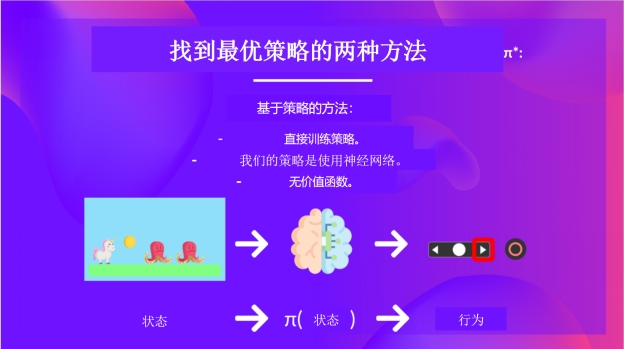
策略以状态为输入，输出在该状态下要采取的动作（确定性策略：给定状态输出一个动作的策略，与随机策略相反，随机策略输出动作的概率分布）。

因此，我们不是直接设定策略的行为；而是通过训练价值函数来间接的确定策略。

• 基于价值的方法： 通过训练一个价值函数来间接地确定策略。这个价值函数会输出一个状态或者状态-动作对的价值。给定这个价值函数，我们的策略将采取相应的动作。

由于策略没有被训练/学习，我们需要指定它的行为。例如，如果我们想要一个策略，使得其满足：给定价值函数，它将总是采取能够带来最大奖励的动作。这意味着我们需要定义一个贪婪策略。

给定一个状态，动作-价值函数会输出在该状态下每个动作的价值。然后，我们预定义的贪心策略会根据状态或状态-动作对选择具有最高价值的动作。

因此，无论我们使用哪种方法来解决问题，我们都要有一个策略。在基于价值的方法中，我们不需要训练策略：策略只是一个简单的预先指定的函数（例如贪婪策略），它使用价值函数给出的值来选择动作。

所以区别在于：

• 在基于策略的方法中，通过直接训练策略来找到最优策略（表示为π*）。
• 在基于价值的方法中，找到最优价值函数（表示为Q*或V*，我们稍后会讨论区别）意味着拥有了最优策略。

其实大多数时候，在基于价值的方法中，我们会使用Epsilon贪心策略来处理探索和利用之间的权衡问题；在本单元第二部分讨论Q-Learning时，我们会谈到这个问题。

所以，现在我们有两种类型的基于价值的函数：

状态价值函数

策略π下的状态价值函数如下所示：

​

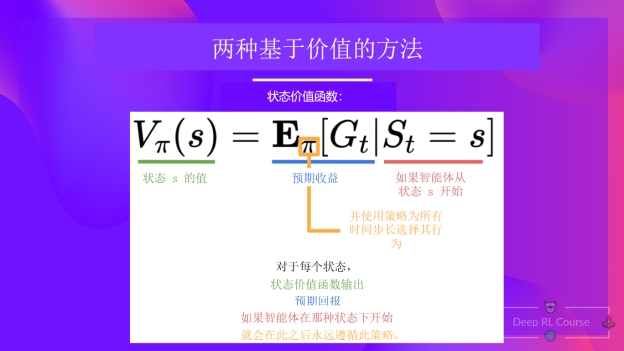
对于每个状态，状态价值函数会输出智能体按照给定策略（也可以理解为所有未来的时间步）从当前状态开始行动所能获得的预期回报。

如果我们取价值为-7的状态：它表示在该状态下按照我们的策略（贪心策略）采取行动，所以是：右，右，右，下，下，右，右。

动作价值函数

在动作-价值函数中，对于每个状态和动作对，动作-价值函数会输出智能体按照给定策略，从当前状态开始行动所能获得的预期回报。

在策略(π)下，智能体在状态(s)中执行动作(a)的价值计算如下所示：

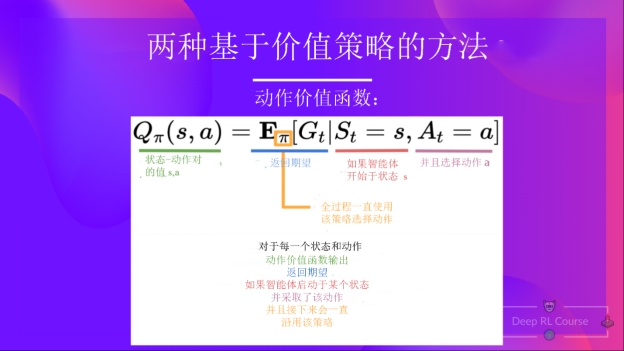
我们可以看到两者之间的区别是：

• 在状态价值函数中，我们计算状态(S_t)的价值
• 在动作价值函数中，我们计算状态-动作对（(S_t, A_t)）的价值，即在该状态下采取该动作的价值。

​

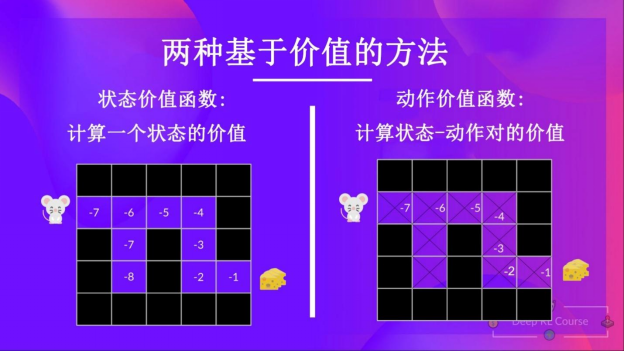
注意：我们没有为动作价值函数示例中的所有状态-动作对都填上数值。

无论哪种情况，无论我们选择哪种价值函数（状态-价值或动作-价值函数），返回的值都是期望回报。

然而，问题是这意味着要计算每个状态或状态-动作对的价值，我们需要求和智能体从该状态开始可以获得的所有奖励。

该过程计算成本可能比较高，所以接下来我们将要用到贝尔曼方程。

贝尔曼方程：简化价值计算

贝尔曼方程简化了状态价值或状态-动作价值的计算。

根据现在所学的，我们知道如果计算 V(S_t) (状态的价值)，那么需要计算在该状态开始并在之后一直遵循该策略的回报。（我们在下面的例子中定义的策略是一个贪心策略；简单起见，我们没有对奖励进行折扣计算）

所以为了计算 V(S_t) ，我们需要计算期望回报的总和。因此：

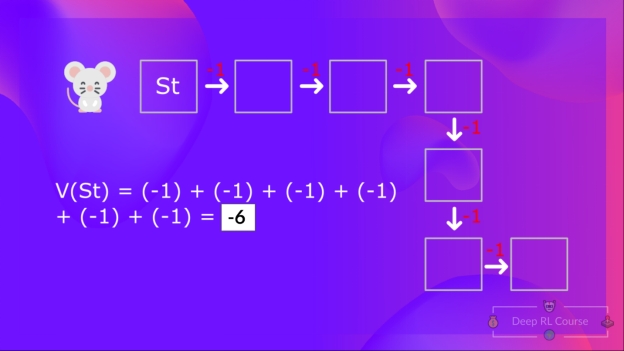
计算状态1的价值：如果智能体从该状态开始，并在之后的时间步中遵循贪心策略（采取能够获取最佳状态值的行动），则把每一步的奖励进行加和

为了计算 （V(S{t+1}) ，我们需要计算在该状态 S{t+1} 的回报。

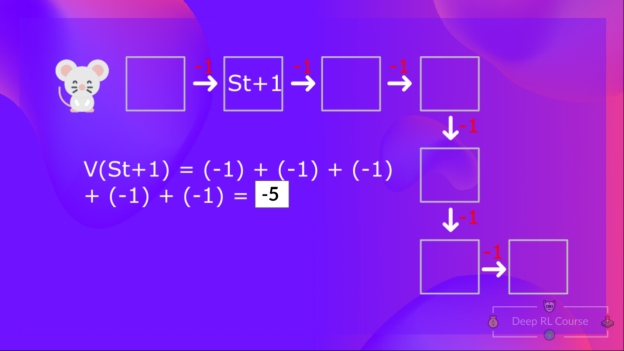
计算状态2的价值：如果智能体在该状态开始行动, 并且在之后的时间步里都遵循该策略，则把每一步的奖励进行加和。

也许你已经注意到了，我们在重复不同的状态价值的计算，如果你要对每一个状态价值或者状态动作价值都重复这种计算那真的是非常无聊。

所以我们用贝尔曼方程来代替对每一个状态或每一个状态动作对求预期回报。（提示：这和动态规划很类似）

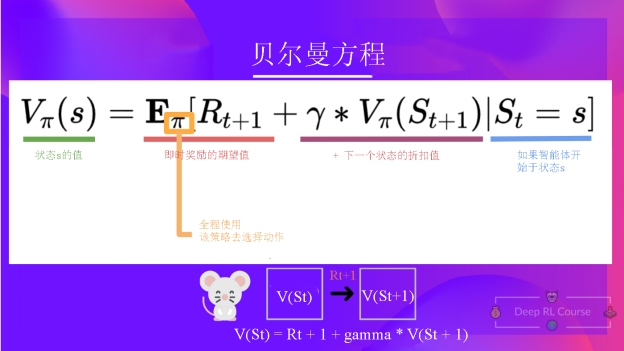
贝尔曼方程是一个递归方程，其大致是这样的：与其从头开始计算每个状态的回报，我们不如将所有状态的价值描述为：

即时奖励 (R{t+1}) + 状态的折扣价值 (gamma * V(S_{t+1}) )

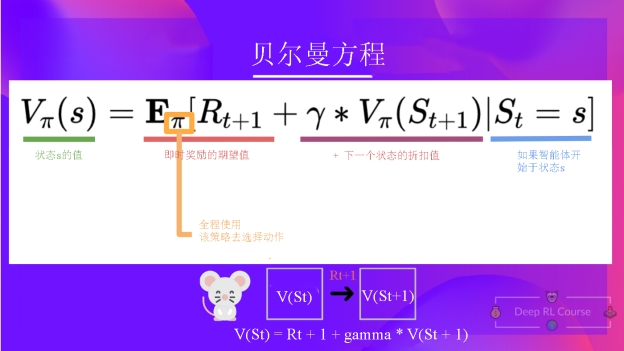
如果我们回顾之前的例子，我们可以认为如果从状态 1 开始行动，那么状态 1 的价值和预期累计回报相等。

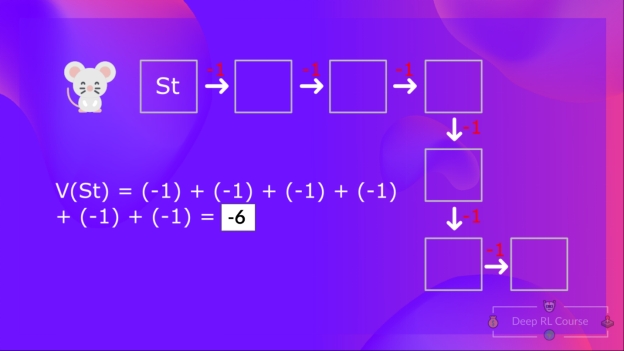
计算状态 1 的价值：如果智能体从状态 1 开始行动，并一直在之后的时间步中遵循该策略，则把每一步的奖励进行加和。

这用公式表示出来就是：V(S{t}) = 当下的即时奖励 R{t+1} + 下个状态的折扣价值 gamma * V(S_{t+1})

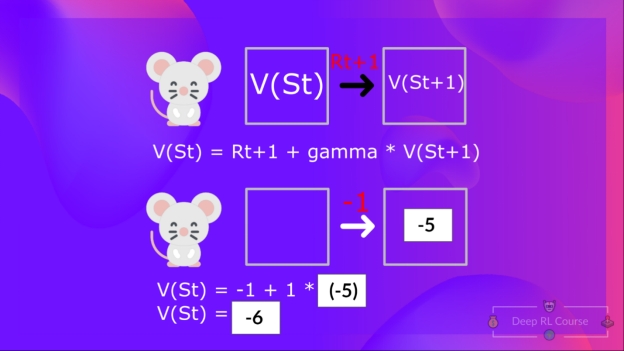
简单起见，我们在这里将gamma设置为1.

为了更简单的阐述原理，在这里我们没有设置折扣率，所以gamma = 1。

但是你将在本单元的Q-learning部分学到一个gamma = 0.99的例子：

• V(S{t+1}) = 当下的即时奖励 (R{t+2}) + 下一个状态的折扣价值 (gamma * V(S_{t+2})
• 诸如此类

现在我们将内容进行回顾，相较于繁琐的计算每一个价值然后最终加和作为预期回报，贝尔曼方程的思想则是对当下即时的奖励和之后状态的折扣价值进行加和从而得到预期回报。

在进入下一节课程前，让我们先思考一下贝尔曼方程中的折扣因子gamma的作用。如果gamma的值非常小会发生什么，如果为1会发生什么？或者gamma非常大假如是一百万，又会发生什么？

蒙特卡罗 VS 时序差分学习

在深入学习Q-Learning算法之前，我们需要先了解一下两种学习策略。

牢记智能体是通过与其环境交互来进行学习的，即给定经验和收到来自环境的奖励，智能体将更新其价值函数或策略。

蒙特卡洛和时序差分学习在训练价值函数或策略函数上是两种不同的策略，但他们都使用经验来解决强化学习问题。

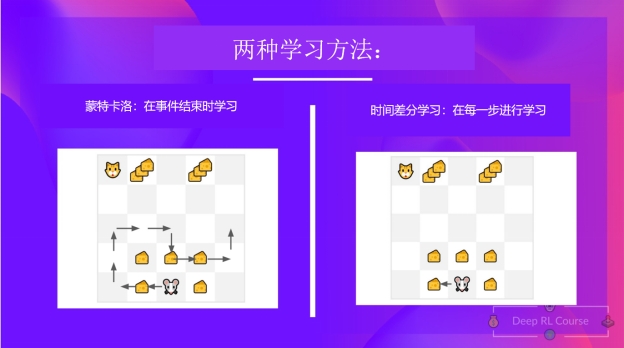
蒙特卡洛在学习之前使用一个完整回合的经验；而时序差分则只使用一个步骤(S_t, A_t, R_{t+1}, S_{t+1})来进行学习。

我们将使用一个基于价值的方法案例来解释他们。

蒙特卡洛：在一个回合结束后进行学习

蒙克卡罗在回合结束时计算(G_t) (回报)并且使用其作为一个更新的目标(V(S_t))。

因此，在更新我们的价值函数之前，它需要一个完整的交互过程。

举个例子：

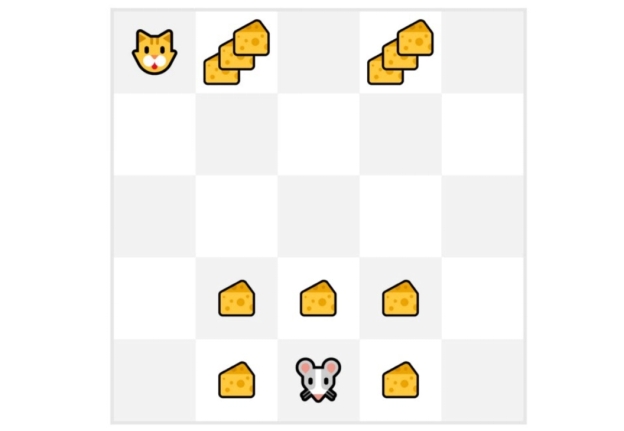
• 我们始终从相同的起点开始新的一轮（episode）。

• 智能体根据策略（policy）选择行动。例如，使用一个 Epsilon Greedy 策略，该策略在探索（随机行动）和利用（利用之前经验）之间交替选择。

• 得到奖励（reward）和下一个状态（next state）。

• 如果猫吃掉老鼠或老鼠移动 > 10 步，则我们将终止该轮。

• 在该轮结束时，我们会得到一个状态、行动、奖励和下一个状态的元组列表。例如 [[状态为第三个瓷砖的底部，向左移动，+1，状态为第二个瓷砖的底部], [状态为第二个瓷砖的底部，向左移动，+0，状态为第一个瓷砖的底部]…]

• 智能体将计算总奖励 (G_t)（以衡量其性能）。

• 然后，它将基于以下公式更新 (V(s_t))。

  

• 最后以这些新知识来重新开始游戏

通过训练的回合越来越多，智能体会把游戏玩的越来越好。

例如，如果用蒙特卡洛训练了一个状态价值函数

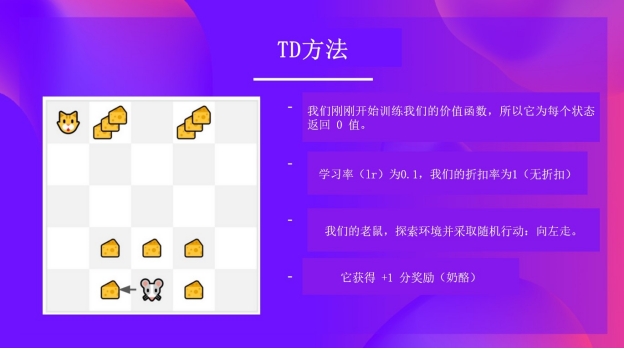
• 我们刚刚开始训练值函数，所以它将为每个状态返回值0。

• 学习率（lr）为0.1，折扣率为1（没有折扣）。

• 小老鼠将探索环境并采取随机动作。

  

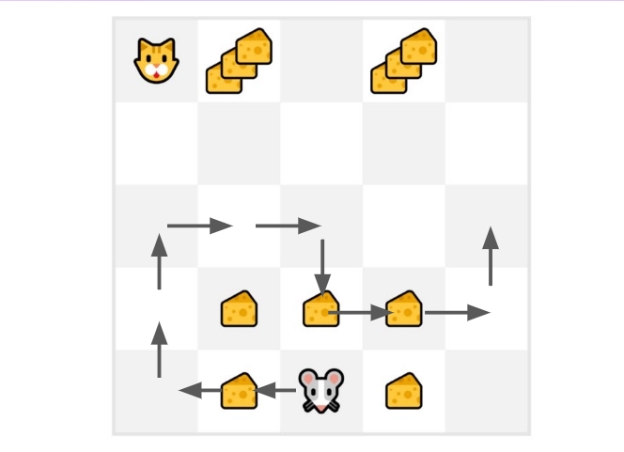
• 小老鼠的移动超过了十步，所以回合结束。

  

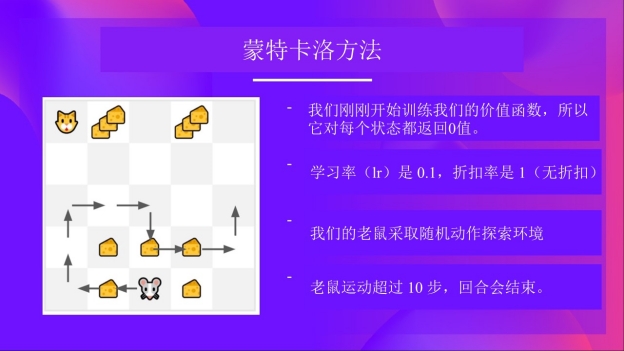
• 我们有一系列的状态、动作、奖励以及下一个状态，所以现在我们需要计算回报（G{t}）

• \(G_t = R_{t+1} + R_{t+2} + R_{t+3} …\)

• \(G_t = R_{t+1} + R_{t+2} + R_{t+3}…\) (为简单起见，我们不对奖励进行折扣计算).

• \(G_t = 1 + 0 + 0 + 0+ 0 + 0 + 1 + 1 + 0 + 0\)

• \(G_t= 3\)

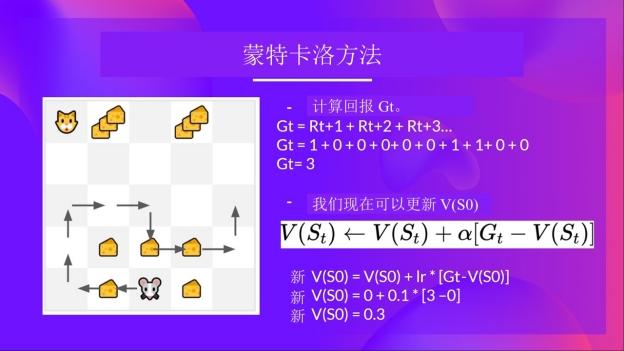
• 现在更新状态(V(S_0)

  

• 新 (V(S_0) = V(S_0) + lr * [G_t — V(S_0)])

• 新 (V(S_0) = 0 + 0.1 * [3 – 0])

• 新 (V(S_0) = 0.3)

  

时序差分算法：在每一步进行学习

另一方面，时序差分学习只需要一次交互（一步）S{t+1}，就可以形成一个TD目标，并使用 R{t+1} 和 γ*V(S_{t+1}) 更新 V(S_t)。

TD算法的思想是在每一步都对 V(S_t) 进行更新。

但是因为我们没有经历整个回合，所以我们没有 (G_t)（期望回报）。相反，我们通过添加 (R_{t+1}) 和下一个状态的折扣值来估计 (G_t)。

这被称为自举（bootstrapping），因为时序差分方法的更新部分是基于现有估值 V(S_{t+1}) 而不是完整样本 (G_t)。

这种方法称为TD(0)或单步TD（在任何单个步骤后更新值函数）。

我们还是以猫和老鼠为例:

• 我们刚刚开始训练我们的价值函数，所以在每个状态都返回0值。

• 我们的学习率是0.1，并且折扣率为1（没有折扣）。

• 小老鼠探索环境并采取随即行为：向左移动

• 他得到了一个奖励 R_{t+1} = 1，因为它吃到了一块芝士

  

  

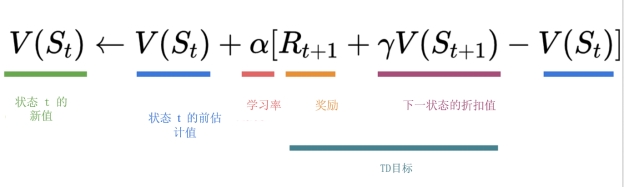
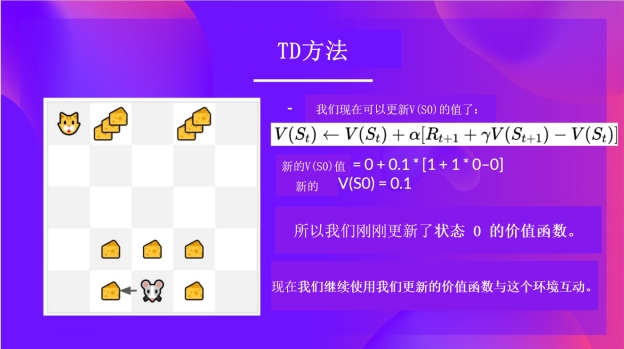
现在我们更新V(S_0)

新 (V(S_0) = V(S_0) + lr * [R_1 + \gamma * V(S_1) - V(S_0)])

新 (V(S_0) = 0 + 0.1 * [1 + 1 * 0–0])

新 (V(S_0) = 0.1)

所以我们从状态0开始更新我们的价值函数。

现在我们持续与这个环境进行交互，并更新价值函数。

总结一下：

• 在蒙特卡洛算法中，我们从完整的回合中更新价值函数，并使用本回合中确定的折扣回报。
• 在时序差分算法中，我们在每一步都对价值函数进行更新，所以我们将还没有获得的 (G_t) 替换为估计回报，即TD-target。

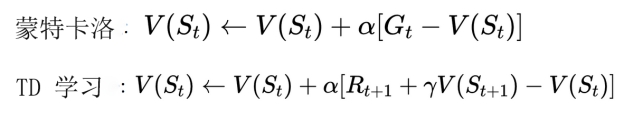
学习进展回顾

在我们深入学习 Q-learning 算法前，先总结一下我们之前都学了什么。

我们学了两种基于价值的函数：

• 状态价值函数：如果智能体在一个给定的状态开始行动，并在之后的行动中一直遵循该策略，则输出该状态的期望回报。
• 动作价值函数：如果智能体在给定的状态开始采取一个给定的行为，并在之后的行动中一直遵循该策略，则输出该状态的期望回报。
• 在基于价值的方法中，相比于学习策略，我们手动定义策略并且学习一个价值函数。如果我们有一个最优价值函数，那就有了一个最优的策略。

还学了两种可以学习价值函数的策略的方法：

• 使用蒙特卡洛方法时，我们从完整的一轮游戏中更新值函数，并且使用该轮游戏的真实、准确的折扣回报。
• 使用TD学习方法时，我们从一个时间步中更新值函数，因此我们用一个被称为TD目标的估计回报替换我们没有的G_t。

学习进展测验

最好的学习方法是对自己进行测试。这能避免过度自信并帮助我们找到需要加强的方面。

Q1: 找到最优策略的两种主要方法是什么？

<Question
choices={[
{
text: “基于策略的方法”,
explain: “使用基于策略的方法，我们直接训练策略来学习在给定状态下采取哪种行动。”,
correct: true
},
{
text: “基于随机的方法”,
explain: “”
},
{
text: “基于价值的方法”,
explain: “使用基于价值的方法，我们训练一个价值函数来学习哪些状态更有价值，并使用该价值函数来选择最优的动作。”,
correct: true
},
{
text: “进化策略方法”,
explain: “”
}
]}
/>

Q2: 什么是贝尔曼方程?

答案

贝尔曼方程是一个递归方程，其工作原理如下：我们不需要从每个状态的起点开始计算回报，而是可以将任意状态的价值视为:

Rt+1 + gamma * V(St+1)

立即奖励 + 之后状态的折扣价值。

Q3: 贝尔曼方程的每个部分的定义是什么?

答案

Q4: 蒙特卡洛（Monte Carlo）方法和时序差分（Temporal Difference, 简称TD）学习方法之间的差异是什么?

<Question
choices={[
{
text: “在使用蒙特卡罗方法时,我们从一个完整的回合中更新价值函数”,
explain: “”,
correct: true
},
{
text: “在使用蒙特卡罗方法时,我们从一个时间步中更新价值函数”,
explain: “”
},
{
text: “在使用TD方法时,我们从一个完整的回合中更新价值函数”,
explain: “”
},
{
text: “在使用TD方法时,我们从一个时间步中更新价值函数”,
explain: “”,
correct: true
},
]}
/>

Q5: 时序差分算法中每一部分的定义是什么?

答案

Q6: 蒙特卡洛算法中每一部分的定义是什么?

答案

恭喜你完成了这个测验🥳，如果你错过了一些要点，花点时间再读一遍前面的部分，以加强你的知识😏。